„Adatszerkezetek” tantárgy , 1. félév
2. előadás’2009
(vázlat)

1. Modulteszt

Azt vizsgáljuk, miként lehetne meggyőződni egy típus megvalósításának helyességéről. Erre ugyan van mód formális, matematikai eszközökkel, most azonban megelégszünk egy empirikus módszerrel: az ún. modulteszttel. A múltkori előadásban többszörösen visszatérő példánk volt a nap típus. Ezt formalizáltuk algebrai, algoritmikus nyelven (export- és megvalósítási modul) és megadtuk kódváltozatát is.

Annak érdekében, hogy ne ad hoc módon (esetleg fontos vizsgálatokat kifelejtve) végezzük a típusmegvalósítás tesztelését, használjuk föl az eddig elkészült specifikációit! Elképzelés a következő:

1. Beillesztünk a modulba egy állapot kijelző rutint, amely képes a típus belső ábrázolásának megfelelő állapot kilistázására (a képernyőre és/vagy fájlba[1]).

2. Készítünk egy tesztelő programot, amelyhez hozzácsatoljuk a vizsgált modult. Deklarálunk megfelelő számú vizsgált típusú változót, és készítünk néhány eljárást, amelyek törzse valamely axióma nyomán keletkezett.

3. Mivel axiómák a HibasE függvényt nem tartalmazzák, ezért ennek helyességét külön tesztelni kell.

4. Mivel a konkrét nyelvi környezet kezdőértékadási szokásai sokszor ismeretlenek, azért a deklaráció utáni alapállapotot is érdemes ellenőrizni. Sőt biztonságos, minden eljárás deklarált változóit használat előtt inicializálni.

Nézzük példának okáért a TNap típust tesztelő programot!

1.Þ A unit-ból kiolvassuk az ábrázolást. Az állapot megjelenítésére most elegendő egy TNap rekordot kiíró eljárást szerkeszteni. Pl.:

Procedure AllapotKi(Const sElo:String; Const n:TNap;
Const sUto:String);
Begin
Write(sElo); {kisérő szöveg; pl. a változó neve}
Write(’ felsKod:’,n.felsKod,’, hiba:’,n.hiba);
Write(sUto); {pl.: soremelés}
ReadKey; {nehogy kifusson a képernyőből}
End;

4. Þ Írunk egy eljárást, amely a deklaráció utáni állapotot jeleníti meg:

Procedure DeklaracioUtan(Const n:TNap);
Begin
AllapotKi(’ Deklaráció után:’,n,’CrLf [2] );
End;

2.Þ Az algebrai specifikációból kicsemegézzük a tesztelésre alkalmas axiómákat: a TNap esetében a 2. kivételével mindet. Most csak a 0-val, 1-gyel, 3-mal és 4-gyel példázzuk a generálási folyamatot.

Procedure Axioma_0;
Var
sz:Word;
mn,mx:TNap;

Begin
Writeln(’0. axióma ----------------------------------’);
{a deklaráció utáni kezdőállapot:}
DeklaracioUtan(mn); DeklaracioUtan(mx);
{a deklaráció utáni inicializálás:}
Inic(mn); Inic(mx);
{a 0. axióma végrehajtása:}
sz:=Szamossag; Min(mn); Max(mx);
{a 0. axiómában szereplők állapotkiírása:}
Writeln(’Számosság’’TNap=’,sz);
AllapotKi(’ Min’’TNap=’,mn,CrLF);
AllapotKi(’ Max’’TNap=’,mx,CrLF);
End;

Procedure Axioma_1;
Var
a:TNap;

Begin
Writeln(’1. axióma ----------------------------------’);
{a deklaráció utáni kezdőállapot:}
DeklaracioUtan(a);
{a deklaráció utáni inicializálás:}
Inic(a);
{az 1. axióma végrehajtása:}
{… nincs mit tenni, a deklarációnál már létrejött …}

{az 1. axiómában szereplők állapotkiírása:}
AllapotKi(’ Létrehoz=’,a,CrLF);
End;

{… a 2. axióma kivitelezhetetlen, nem foglalkozunk vele …}

Procedure Axioma_3;
Var
elo,kov:TNap;

Begin
Writeln(’3. axióma ----------------------------------’);
{a deklaráció utáni kezdőállapot:}
DeklaracioUtan(elo); DeklaracioUtan(kov);

{a deklaráció utáni inicializálás:}
Inic(elo); Inic(kov);

{a 3. axióma végrehajtása:}
Elozo(Hetfo,elo); Kovetkezo(Vasarnap,kov);
{a 3. axiómában szereplők állapotkiírása:}
AllapotKi(’ Elozo(Hetfo)=’,elo,CrLF);
AllapotKi(’ Kovetkezo(Vasarnap)=’,kov,CrLF);
End;

Procedure Axioma_4;
Var
n,kov,elo:TNap;
nK:Integer;

Begin
Writeln(’4. axióma ----------------------------------’);
{a deklaráció utáni kezdőállapot:}
DeklaracioUtan(n); … DeklaracioUtan(elo);
{a deklaráció utáni inicializálás:}
Inic(n); Inic(kov); Inic(elo);
{a 4. axióma végrehajtása:}
n:=Hetfo;
Kovetkezo(n,kov);
{a 4. axiómában szereplők állapotkiírása:}
AllapotKi(’ n=’,n,’’);
AllapotKi(’ Kovetkezo(n)=’,kov,’’);
For nK:=1 to 5 do {keddtől szombatig}
Begin
n.felsKod:=nK; {kihasználjuk a Pascal unit nyitottságát}
Kovetkezo(n,kov); Elozo(n,elo);
{a 4. axiómában szereplők állapotkiírása:}
AllapotKi(’ n=’,n,’’);
AllapotKi(’ Kovetkezo(n)=’,kov,’’);
AllapotKi(’ Elozo(n)=’,elo,CrLF);
End;
n:=Vasarnap;
Elozo(n,elo);
{a 4. axiómában szereplők állapotkiírása:}
AllapotKi(’ n=’,n,’’);
AllapotKi(’ Elozo(n)=’,elo,’’);
{hiba-vizsgálat:}
Writeln(’Hibavizsgálatok:’);
n:=Hetfo; Elozo(n,elo);
AllapotKi(’ n=’,n,’’);
AllapotKi(’ Elozo(n)=’,elo,CrLf);
n:=Vasarnap; Kovetkezo(n,kov);
AllapotKi(’ n=’,n,’’);
AllapotKi(’ Kovetkezo(n)=’,kov, CrLf);
End;
…

Az axiómák mellett azonban a HibasE függvény helyességét még körültekintően tesztelni kell!

Ezek után a főprogram lényegileg az egyes axiómák hívásából áll.

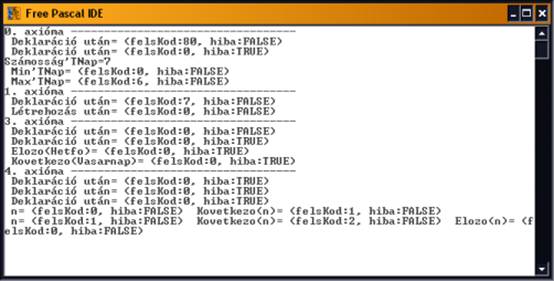
A tesztelő program futás közben.

2. A Tömb típuskonstrukció

2.1. A tömb algebrai specifikációja

Típus Tömb(Index:Elem):

Asszociált műveletek:

Létrehoz:Tömb
Lerombol(Tömb)
ElemSzám(Tömb):Egész
ElemÉrték(Tömb,Index):Elem È {NemDef}
ElemMódosít(Tömb,Index,Elem):Tömb
Axiómák:

t: Tömb(Index:Elem) = tetszőleges tömbtípusú objektum

i,j: Index = tetszőleges indextípusú objektum

e: Elem = tetszőleges elemtípusú objektum

1^o A Létrehozás után a tömb minden eleme olyan értékű, amilyent a bázistípus Létrehoz_e művelete létrehoz[3]. Pontosan annyi eleme lesz, amennyit az Index-típus meghatároz.

ElemÉrték(Létrehoz,i)=Létrehoz_e Ù ElemSzám(Létrehoz)=Számosság(Index)

Állítás:
Egy elemének módosítása nem változtatja meg a tömb hosszát, azaz

ElemSzám(ElemMódosít(t,i,e))=ElemSzám(t)

Biz.:
1^o Þ Számosság(Index)=Konstans
Þ t’=ElemMódosít(t,i,e) Ù ElemSzám(t’)=Számosság(Index)
Þ ElemSzám(t’)=ElemSzám(t)

2^o Lerombolás után nincs értelme a műveletek (a Létrehoz kivételével) alkalmazásának. (Ez egy nyilvánvalóságot megfogalmazó axióma, l. a szignatúrákat!)

ElemSzám(Lerombol(t))=NemDef Ù …

3^o A tömb elemének az az értéke, amit az utolsó rávonatkozó ElemMódosít művelet adott neki.

ElemÉrték(ElemMódosít(t,i,e),i)=e

4^o Az elemek értéküket módosításig megőrzik. (Ez egy szokatlan axióma, amely azt mondja meg, hogy az ElemMódosítás művelet mire nincs hatással; a későbbi sorozatfélékhez képest jellemző eltérés.)

i¹j Þ ElemÉrték(ElemMódosít(t,i,e),j)=ElemÉrték(t,j)

Állítás:
a tömb létrehozása után az egyes elemei az első ElemMódosít-ig kezdőértékükkel rendelkeznek.

Biz.:
a 3^o és az 4^o folyamánya.

Megjegyzések:

• Az egyetlen kezelési anomáliáról, az indextúllépésről nem kell rendelkezni az axiómákban, hiszen ez az egyik bázistípust érintő sértés lévén már korábban –az Index-típushoz tartozó axiómák megsértése miatt– hibás, azaz nem definiált eredményre vezetne.
• A 2^o axióma egy szintaktikai képtelenséget fogalmaz meg: a Lerombol függvény „eredményére” lehetetlen más függvényt alkalmazni, hisz nincs mire, nincs értékkészlete! Ez persze nem a tömb típuskonstrukciós eszköz specifikus problémája, minden lerombol függvényé. Ezért nem is jeleztük külön a többi művelet értékkészleténél a NemDef értéket. S ezt a további típuskonstrukcióknál már nem is említjük.
• Ehhez hasonlóan lehetne a több-indexes tömbökkel szembeni elvárásunkat megfogalmazni, amitől eltekintünk.

2.2. A tömb algoritmikus specifikációja

Az eltérő paraméterezési szokások miatt külön-külön fogalmazzuk meg az 1- és a 2-indexes tömbök, azaz a vektorok és a mátrixok típuskonstrukcióját. (A többieket specifikálni ezek alapján már gyerekjáték.)

2.2.1. A tömb exportmoduljai

Először a vektor exportmodulját adjuk meg:

ExportModul Tömb(Típus TIndex: Típus TElem):
[Ef: TIndex: diszkrét, sőt véges típus (így van neki „Sorszám”, „Következő”
… függvénye)[4],
TElem típushoz asszociáltunk „Létrehoz”, „=”, „Be”, „Ki”… műveleteket,
az Ef-Uf-ben a t-t mint e-k sorozatát tekintjük, elemeit 1-től indexelve]

Eljárás Létrehoz(Változó t:Tömb)
Ef: Ø$tÎTömb
Uf: "iÎTIndex: $eÎTElem: t(Sorszám(i)+1)=e Ù
Létrehoz(e).Uf

Eljárás Lerombol(Változó t:Tömb)
Ef: $tÎTömb
Uf: Ø$tÎTömb

Függvény ElemSzám(Konstans t:Tömb):Egész
Ef: $tÎTömb
Uf: ElemSzám(t)=Számosság’TIndex

Operátor ElemÉrték(Konstans t:Tömb, i:TIndex):TElem
Másnéven t(i)
Ef: $tÎTömb
Uf: ElemÉrték(t,i)=t(Sorszám(i)+1)

Operátor ElemMódosít(Változó t:Tömb,
Konstans i:TIndex, e:TElem)
Másnéven t(i):=e
Ef: $tÎTömb
Uf: t’(Sorszám(i)+1)=e Ù
"j¹iÎTIndex: t(Sorszám(j)+1)=t’(Sorszám(j)+1)

Infix Operátor Egyenlő(Konstans t,tt:Tömb):Logikai
Másnéven t=tt
Ef: $t,ttÎTömb
Uf: Egyenlő(t,tt)=
( "iÎTIndex: t(Sorszám(i)+1)=tt(Sorszám(i)+1) )

Infix Operátor LegyenEgyenlő(Változó t:Tömb
Konstans tt:Tömb)
Másnéven t:=tt
Ef: $t,ttÎTömb
Uf: "iÎTIndex: t’(Sorszám(i)+1)=tt(Sorszám(i)+1) Ù
"iÎTIndex: tt(Sorszám(i)+1)=tt’(Sorszám(i)+1)

Operátor Be(Változó t:Tömb)
Másnéven Be:t
Ef: $tÎTömb Ù "iÎTIndex: Be(t(Sorszám(i)+1)).Ef [5]
Uf: "iÎTIndex: Be(t’(Sorszám(i)+1)).Uf

Operátor Ki(Konstans t:Tömb)
Másnéven Ki:t
Ef: $tÎTömb
Uf: "iÎTIndex: Ki(t(Sorszám(i)+1)).Uf

Függvény Hibás?(Változó t:Tömb):Logikai
Ef: $tÎTömb
Uf: Hibás?(t)=volt-e elkövetett és nem letesztelt hiba

Modul vége.

Megjegyzések:

• Jól látszik, hogy az elő- és utófeltételekben visszanyúltunk a TIndex és TElem típusokhoz. Az „=”, az „.Ef” és az „.Uf” a megfelelő típus megfelelő műveletére, illetőleg annak elő-utófeltételére utal.
• A feltételekben sokszor fordul elő a t(Sorszám(i)+1) kifejezés. Itt a t(x) a t-nek, mint sorozatnak az x. elemét jelenti, tehát nem keverendő össze a „hagyományos” t-tömb elemindexeléssel. A Sorszám(i)+1 konverzióval képezzük az i index értékét 1..Számosság’TIndex közé, azaz szokásos sorozatindexszé.

Következzék a mátrix exportmodulja, amelyet rövidítve (ef-uf nélkül) mellékelünk. Értelemszerű módosításokkal megkapható a precíz változat is.

ExportModul Tömb(Típus TIndex₁,TIndex₂: Típus TElem):

Eljárás Létrehoz(Változó t:Tömb)

Eljárás Lerombol(Változó t:Tömb)

Függvény ElemSzám(Konstans t:Tömb):Egész

Operátor ElemÉrték(Konstans t:Tömb,
i:TIndex₁,j:TIndex₂):TElem
Másnéven t(i,j)

Operátor ElemMódosít(Változó t:Tömb,
Konstans i:TIndex₁,j:TIndex₂,
e:TElem)
Másnéven t(i,j):=e

Infix Operátor Egyenlő(Konstans t,tt:Tömb):Logikai
Másnéven t=tt

Infix Operátor LegyenEgyenlő(Változó t:Tömb
Konstans tt:Tömb)
Másnéven t:=tt

Operátor Be(Változó t:Tömb)
Másnéven Be:t

Operátor Ki(Konstans t:Tömb)
Másnéven Ki:t

Függvény Hibás?(Változó t:Tömb):Logikai

Modul vége.

2.2.2. A tömb reprezentációs-implementációs modulja

Kétféle ábrázolást veszünk szemügyre. Az első az ún. folytonos ábrázolás, amelyben a tömb elemei egymásután, szorosan foglalnak helyet, a másikban a rákövetkezési kapcsolatot láncolással (mutatókkal) biztosítjuk.

Az alábbi néhány fogalmat sűrűn használjuk.

Operátor Számosság(Típus t):Egész
Másnéven Számosság’t
[a t típus konstansainak száma]

Operátor Méret(Típus t):Egész
Másnéven Méret’t
[a t típus folytonos ábrázolásához szükséges memória mérete]

Függvény Sorszám(Konstans x:Típus):Egész
[az x Típus-beli belsőábrázolású kódja, azaz 0-tól induló sorszáma]

Függvény Cím(Konstans x:Típus):Egész
[az x Típus-ú adat memória címe]

A folytonos ábrázolás

Egy „naiv”, értsd: leegyszerűsített memóriamodellre építjük a leírást. Az alábbiakban összefoglaljuk azokat a fogalmakat, amelyeket alapfogalmaknak tekintünk, s ezekre építjük föl a folytonos ábrázolást. (Az egész mögé egy, az alábbi operátorok által kezelt byte-sorozatot kell képzelnünk, amelyek byte-jait természetes számokkal indexelhetünk.)

Konstans
MaxMem:Egész(???)
Típus
MemóriaCím=0..MaxMem [Ì Egész,
az Egész műveleteit használni fogjuk]

Konstans
Sehova:MemóriaCím(0)

Eljárás Lefoglal(Változó tmut:MemóriaCím,
Konstans db:Egész)
[a memóriában db-nyi helyet foglal,
a kezdőcímet tmut-ba adja vissza,
ha nem sikerült, akkor Sehova-t]

Eljárás Felszabadít(Változó tmut:MemóriaCím,
Konstans db:Egész)
[a tmut-nál kezdődő db-nyi hosszú
memóriatartományt felszabadítja,
tmut-ba Sehova-t tesz]

Eljárás Értékmásolás(Konstans db:Egész,
c₁:MemóriaCím,
c₂:MemóriaCím)
[a c₁ címre másol db darabnyi byte-ot
a c₂ címtől kezdődően]

Először a vektor modulját adjuk meg:

Modul Tömb(Típus TIndex: Típus TElem):

Reprezentáció

Változó
kcím:MemóriaCím
hiba:Logikai

Implementáció

Eljárás Létrehoz(Változó v:Tömb):

Ef: kcím=Sehova[6] [Ø$tÎTömb]
Uf: "iÎTIndex: $eÎTElem: t(Sorszám(i)+1)=e Ù
Létrehoz(e).Uf

Változó i:TIndex
e:TElem
kc:MemóriaCím

Lefoglal(kcím,Számosság’TIndex*Méret’TElem)

Ha kcím=Sehova akkor
hiba:=Igaz

különben
hiba:=Hamis
Létrehoz(e) [visszavezetés a Létrehoz(TElem)-re,
és nem foglalkozunk az e-hibákkal!]
kc:=ElemCím(v,Min’TIndex) [ºkcím; tömb-kezdőcím]
Ciklus i=1-től Számosság’TIndex-ig
Értékmásolás(Méret’TElem,kc,Cím(e))
kc:+Méret’TElem
Ciklus vége
Elágazás vége
Eljárás vége.

Eljárás Lerombol(Változó v:Tömb):
Ef: kcím¹Sehova [$tÎTömb]
Uf: kcím=Sehova [Ø$tÎTömb]

Felszabadít(kcím,Számosság’TIndex*Méret’TElem)
Eljárás vége.

Függvény ElemSzám(Változó v:Tömb):Egész
Ef: kcím¹Sehova [$tÎTömb]
Uf: ElemSzám(t)=Számosság’TIndex

ElemSzám:=Számosság’TIndex
Függvény vége.

Operátor ElemÉrték(Konstans v:Tömb, i:TIndex):TElem
Másnéven t(i)
Ef: kcím¹Sehova [$tÎTömb]
Uf: ElemÉrték(t,i)=t(Sorszám(i)+1)

Értékmásolás(Méret’TElem,
Cím(ElemÉrték),
ElemCím(v,i))
[ElemÉrték:=TElem(ElemCím(v,i))]
Operátor vége.

Operátor ElemMódosít(Változó v:Tömb,
Konstans i:TIndex, e:TElem):
Másnéven t(i):=e
Ef: kcím¹Sehova [$tÎTömb]
Uf: t’(Sorszám(i)+1)=e Ù
"j¹iÎTIndex: t(Sorszám(j)+1)=t’(Sorszám(j)+1)

Értékmásolás(Méret’TElem,
ElemCím(v,i),
Cím(e))
[TElem(ElemCím(v,i)):=e]
Operátor vége.

Infix Operátor Egyenlő(Konstans t,tt:Tömb):Logikai
Másnéven t=tt
Ef: t.kcím¹Sehova Ù tt.kcím¹Sehova [$t,ttÎTömb]
Uf: Egyenlő(t,tt)=
( "iÎTIndex: t(Sorszám(i)+1)=tt(Sorszám(i)+1) )

[hf.]

Infix Operátor LegyenEgyenlő(Változó t:Tömb
Konstans tt:Tömb)
Másnéven t:=tt
Ef: t.kcím¹Sehova Ù tt.kcím¹Sehova [$t,ttÎTömb]
Uf: "iÎTIndex: t’(Sorszám(i)+1)=tt(Sorszám(i)+1) Ù
"iÎTIndex: tt(Sorszám(i)+1)=tt’(Sorszám(i)+1)

[hf.]

Operátor Be(Változó t:Tömb)
Másnéven Be:t
Ef: kcím¹Sehova [$tÎTömb] Ù
"iÎTIndex: Be(t(Sorszám(i)+1)).Ef
Uf: "iÎTIndex: Be(t’(Sorszám(i)+1)).Uf

[hf.]

Operátor Ki(Konstans t:Tömb)
Másnéven Ki:t
Ef: kcím¹Sehova [$tÎTömb]
Uf: "iÎTIndex: Ki(t(Sorszám(i)+1)).Uf

[hf.]

Függvény Hibás?(Változó t:Tömb):Logikai

[hf.]

[„lokális” függvények:]

Függvény ElemCím(Konstans v:Tömb, i:TIndex):MemóriaCím
ElemCím:=kcím+RelatívCím(i)
Függvény vége.

Függvény RelatívCím(Konstans i:TIndex):Egész
RelatívCím:=Sorszám(i)*Méret’TElem
Függvény vége.

Inicializálás

kcím:=Sehova; hiba:=Hamis

Modul vége.

A mátrix modulja, rövidítve:

Modul Tömb(Típus TIndex₁,TIndex₂: Típus TElem):

Reprezentáció

Változó
kcím:MemóriaCím
hiba:Logikai

Implementáció

Eljárás Létrehoz(Változó m:Tömb):

Lefoglal(kcím,
Számosság’TIndex₁*
Számosság’TIndex₂*
Méret’TElem)

Ha kcím=Sehova akkor
hiba:=Igaz
különben
hiba:=Hamis
[hf.]
Elágazás vége
Eljárás vége.

Eljárás Lerombol(Változó m:Tömb):
Felszabadít(kcím,Számosság’TIndex₁*
Számosság’TIndex₂*
Méret’Elem)
Eljárás vége.

Függvény ElemSzám(Változó v:Tömb):Egész
ElemSzám:=Számosság’TIndex₁*Számosság’TIndex₂
Függvény vége.

Operátor ElemÉrték(Konstans m:Tömb,
i₁:TIndex₁, i₂:TIndex₂):TElem
Értékmásolás(Méret’TElem,
Cím(ElemÉrték),
ElemCím(m,i₁,i₂))
[ElemÉrték:=TElem(ElemCím(m,i₁,i₂))]
Operátor vége.

Operátor ElemMódosít(Változó m:Tömb,
Konstans i₁:TIndex₁,i₂:TIndex₂,
e:TElem):
Értékmásolás(Méret’TElem,
ElemCím(m,i₁,i₂),
Cím(e))
[TElem(ElemCím(m,i₁,i₂)):=e]
Operátor vége.

…

[„lokális” függvények:]

Függvény ElemCím(Konstans m:Tömb,
i₁:TIndex₁,
i₂:TIndex₂):MemóriaCím
ElemCím:=kcím+RelatívCím(i₁,i₂)
Függvény vége.

Függvény RelatívCím(Konstans i₁:TIndex₁,
i₂:TIndex₂):Egész
RelatívCím:=(Sorszám(i₁)*Számosság’TIndex₁+
Sorszám(i₂))*Méret’TElem
Függvény vége.

Inicializálás

kcím:=Sehova; hiba:=Hamis

Modul vége.

Továbbiakban, ha folytonos ábrázolásról beszélünk, mindig az itt definiált tömbös ábrázolásra gondolunk (nem a „naiv” memóriamodellre).

A láncolt ábrázolás

Most is az ábrázolás alapmodelljét tisztázzuk először:

Típus
MemóriaCím=Típ’Mutató [alapfogalom: minden típushoz a megfelelő]

Konstans
Sehova:MemóriaCím(???)

Függvény Típ(Konstans m:MemóriaCím):Típ
[konstrukciós függvény, amely az m-től kezdődően
„egybefüggően” jelenti az adott típusú adatot]

Operátor Típ(Változó m:MemóriaCím, Konstans e:Típ)
Másként Típ(m):=e
[értékadás operátor, amely az m-től kezdődően
az adott típusú adatba az e értéket másolja]

Eljárás Lefoglal(Változó tmut:Típ’Mutató)
[a memóriában „Típ”-nyi helyet foglal,
és Típ-nek megfelelő kézdőértékre állít,
a kezdőcímet tmut-ba adja vissza,
ha nem sikerült, akkor Sehova-t]

Eljárás Lefoglal(Változó tmut:Típ’Mutató,
Konstans kért:Típ)
[a memóriában „Típ”-nyi helyet foglal,
majd a kért kezdőértékkel föltölti,
a kezdőcímet tmut-ba adja vissza,
ha nem sikerült, akkor Sehova-t]

Eljárás Felszabadít(Változó tmut:Típ’Mutató)
[a tmut-nál kezdődő „Típ”-nyi hosszú
memóriatartományt felszabadítja,
tmut-ba Sehova-t tesz]

A vektor modulja:

Modul Tömb(Típus TIndex: Típus TElem):

Reprezentáció

Típus [„lokális” típusok!]
TVektorElem=Rekord(ért:TElem,köv:TVektorElem’Mutató)
TVekEleMut=TVektorElem’Mutató

Változó
kcím:TVekEleMut
hiba:Logikai

Implementáció

Eljárás Létrehoz(Változó v:Tömb):
Változó
i:Egész
hol:TVekEleMut

Lefoglal(kcím) [figyelem: ha létre tud jönni, akkor kap kezdőértéket!]
Ha kcím<>Sehova akkor
hiba:=Hamis
hol:=kcím [az első elem létrejött, az ő címe a tömb kezdőcíme]
i:=1
Ciklus amíg i<Számosság’TIndex és nem hiba
Lefoglal(TVektorElem(hol).köv)[figyelem:kap kezdőértéket!]
hol:=TVektorElem(hol).köv
hiba:=hol=Sehova [nincs több hely]
Ciklus vége [a további elemek is létrejöttek]
Ha hiba akkor
[hf.: kcím-től kezdve felszabadítjuk a lefogalt helyet]
különben
TVektorElem(hol).köv:=Sehova [utolsó után nincs több elem]
[ez elhagyható, mert automatikusan Sehova címmel jött létre[7]]
Elágazás vége
különben
hiba:=Igaz
Elágazás vége
Eljárás vége.

Eljárás Lerombol(Változó v:Tömb):
Változó
i:TIndex
hol:TVekEleMut

hol:=TVektorElem(kcím).köv [a törlendő utánira mutat]
Ciklus i=Min’TIndex-től Max’TIndex-1-ig
Felszabadít(kcím) [az akt. elsőt töröltük]
kcím:=hol [a törlendőre állítás]
hol:=TVektorElem(kcím).köv [a törlendő utánira mutat]
Ciklus vége
Felszabadít(kcím) [az utolsót töröltük]
[kcím=Sehova!]
Eljárás vége.

Operátor ElemÉrték(Konstans v:Tömb, i:TIndex):TElem
ElemÉrték:=TElem(ElemCím(v,i))
Operátor vége.

Operátor ElemMódosít(Változó v:Tömb,
Konstans i:TIndex, e:TElem):
TElem(ElemCím(v,i)):=e
Operátor vége.

…

[„lokális” függvény:]

Függvény ElemCím(Konstans v:Tömb,
i:TIndex):TVekEleMut
Változó
j:Egész
hol:TVekEleMut

hol:=kcím
Ciklus j=1[!]-től Sorszám(i)-ig
hol:=TVektorElem(kcím).köv
Ciklus vége
ElemCím:=hol
Függvény vége.

Inicializálás

kcím:=Sehova; hiba:=Hamis

Modul vége.

A mátrix modulja az alábbi. Ötlete: a mátrix elemeinek „kiegyenesítése”, azaz a mátrix-sorok egymásután fűzése (sorfolytonos láncolt ábrázolás):

Modul Tömb(Típus TIndex₁,TIndex₂: Típus TElem):

Reprezentáció

Típus [„lokális” típusok!]
TMátrixElem=Rekord(ért:TElem,köv:TMátrixElem’Mutató)
TMatEleMut=TMátrixElem’Mutató

Változó
kcím:TMatEleMut
hiba:Logikai

Implementáció

Eljárás Létrehoz(Változó v:Tömb):
Változó
i:Egész
hol:TMatEleMut

Lefoglal(kcím); hol:=kcím [az első elem létrejött]
Ciklus i=2-től Számosság’TIndex₁*Számosság’TIndex₂-ig
Lefoglal(TMátrixElem(hol).köv)
hol:=TMátrixElem(hol).köv
Ciklus vége [a további elemek is létrejöttek]
Eljárás vége.

Eljárás Lerombol(Változó v:Tömb):
Változó
i:Egész
hol:TMatEleMut

hol:=TMátrixElem(kcím).köv [a törlendő utánira mutat]
Ciklus i=1-től Számosság’TIndex₁*Számosság’TIndex₂-1-ig
Felszabadít(kcím) [az aktuális elsőt töröltük]
kcím:=hol [kcím a törlendőre állítása]
hol:=TMátrixElem(kcím).köv [a törlendő utánira mutat]
Ciklus vége
Felszabadít(kcím) [az utolsót töröltük]
[kcím=Sehova!]
Eljárás vége.

Operátor ElemÉrték(Konstans v:Tömb,
i₁:TIndex₁,
i₂:TIndex₂):TElem
ElemÉrték:=TElem(ElemCím(v,i₁,i₂))
Operátor vége.

Operátor ElemMódosít(Változó v:Tömb,
Konstans i₁:TIndex₁,
i₂:TIndex₂, e:TElem):
TElem(ElemCím(v,i₁,i₂)):=e
Operátor vége.

…

[„lokális” függvény:]

Függvény ElemCím(Konstans v:Tömb,
i₁:TIndex₁,
i₂:TIndex₂):TMatEleMut
Változó
j:Egész
hol:TMatEleMut

hol:=kcím
Ciklus j=1[!]-től Sorszám(i₁)*Számosság’TIndex₁+
Sorszám(i₂)-ig
hol:=TMátrixElem(kcím).köv
Ciklus vége
ElemCím:=hol
Függvény vége.

Inicializálás

kcím:=Sehova; hiba:=Hamis

Modul vége.

2.3. Speciális tömbök

2.3.1. A „specialitás” mibenlétéről

Speciális tömbnek most azt tekintjük, amely elemei rendelkeznek helycsökkentő tulajdonsággal:

1. van olyan elemérték, amely gyakoriságánál fogva „dominánsnak” tekinthető,

2. van néhány olyan eleme, amellyel a többiek generálhatók.

Általános ötlet a reprezentációra:

1. csak egyszer (vagy egyszer sem) tárolni az ismétlődőt,

2. csak a „báziselemeket” tárolni.

Két aleset az 1.-hez:

· szisztematikusan elhelyezkedő dominánselem,

· rendszertelenül, elszórtan elhelyezkedő ismétlődő elem.

2.3.2. Szisztematikusan elhelyezkedő elemek tömbökben

Ötlet: a domináns elemet egy példányban tárolva a nem ismétlődők előtt (vagy után), és a címkiszámító függvény olyan definiálása, hogy az adott indexhez a tárolt elem indexét adja.

Az ilyen fajta tömböknek érdekes alkalmazása a négyzetes szám-mátrixok (TIndex₁= =TIndex₂) között található:

· alsó-/felső-háromszög mátrix;

· szimmetrikus mátrix;

· tridiagonális vagy Jacobi-féle mátrix (amelyben csak a főátlóban és balról, jobbról közvetlen mellette álló elemek nem 0-k);

· Toeplitz-féle mátrix (amelynek minden, a főátlóval párhuzamos „átlói” mentén csupa azonos értéke van);

· Hänkel-féle mátrix (hasonlatos a Toeplitz-hez, de a mellékátlóval párhuzamos irányban).

Reprezentációhoz:

Típus TSziszVektIndex=0[a domináns indexe]..Helyszükséglet
TSziszVekt=Tömb(TSziszVektIndex:TElem)

Implementációhoz:

Függvény Index(Konstans i,j:TIndex):TSziszVektIndex
Index:=a mátrix (i,j) elemének TSziszVekt-beli
indexe
Függvény vége.

Például a MaxN*MaxN-es alsó-háromszög mátrix esetén:

Típus T3szögMIndex=0..MaxN*(MaxN-1) div 2
T3szögMátrix=Tömb(T3szögMIndex:TElem)

Függvény Index(Konstans i,j:TIndex):T3szögMIndex
Ha i>j akkor Index:=Sorszám(i)*(Sorszám(i)+1)
div 2 + Sorszám(j) + 1
különben Index:=0
Függvény vége.

Gondolja meg a többi művelet mennyiben változik, ill. a többi speciális mátrix esetén az ábrázolás és az index(transzformációs) függvény hogyan definiálható.

2.3.3. Hiányosan kitöltött tömbök

Ötlet: mivel nincs rendszer a tárolandó elemek hollétében, ezért tárolni kell a nem ismétlődő elemek indexét (indexeit) is.

Egy ilyen „tömör” vektor ábrázolása és kezelésének alapjául szolgáló indextranszformációs függvénye:

Típus TTömörIndex=0[a domináns indexe]..Helyszükséglet
TTömörElem=Rekord(érték:TElem,index:TIndex)
TTömörVektor=Tömb(TTömörIndex:TTömörElem)

Függvény Index(Konstans v:TTömörVektor,
i:TIndex):TTömörIndex
Index:=Kiválasztás(v(k).index kÎTTömörIndex, =i?)
Függvény vége.

A mátrix esetében hasonlóan gondolkodhatunk:

Típus TTömörIndex=0..helyszükséglet
TTömörElem=Rekord(érték:TElem,sor,oszl:TIndex)
TTömörMátrix=Tömb(TTömörIndex:TTömörElem)

Függvény Index(Konstans m:TTömörMátrix,
i,j:TIndex): TTömörIndex
Index:=Kiválasztás((m(k).sor,m(k(.oszlop) kÎTTömör-
Index, =(i,j)?)
Függvény vége.

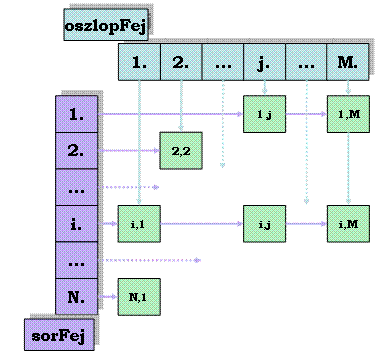
Az elemek „elérése” így lineárisan hosszú lehet a mátrix jobb-alsó sarka felé haladva (feltéve az indexek szerinti rendezettséget). Ezen lehet segíteni az ún. ortogonális ábrázolással (vagyis egyfajta láncolt ábrázolással). Az alábbi rajz mutatja a lényeget:

Hiányos mátrix ortogonális ábrázolása

2.3.4. Generálható elemek tömbökben

Helytakarékosságot olyan tömbök esetében, amelyek elemei néhány kiemelt segítségével generálhatók nyilvánvalóan olymódon érhetünk el, hogy az ábrázolásnál csak a bázis elemekre szorítkozunk. Mivel a többi elemre az érték helyett a kiszámítás szabálya kell ismert legyen, akkor tudunk spórolni a hellyel, ha a szabályhozzárendelést elemcsoportokra tudjuk „göngyölítve” kifejezni. Ez azt is jelenti, hogy valamiféle topologikus szisztematikusságnak is létezni kell. Ekkor a megvalósításhoz csak a bázis elemek tárolása és az indexek alapján működő generáló függvény szükséges.

Egy jellegzetes példa a Vandermonde-mátrix (TIndex₁=1..N, TIndex₂=1..M, TElem= =Valós):

1. 2. 3. … M.

1.: 1 1 1 … 1

2.: a₁ a₂ a₃ … a_M

3.: a₁² a₂² a₃² … a_M²

... ... …

N.: a₁^N-1 a₂^N-1 a₃^N-1 … a_M^N-1

Típus TVanderMátrix=Tömb(TIndex₂:Valós)
[a generáló elemek a 2. sorban]

Függvény Vander(Konstans v:TVanderMátrix,
i:TIndex₁,j:TIndex₂):Valós
Ha i=1 akkor Vander:=1
különben Vander:=v(j)^j-1
Függvény vége.

Tartalom

„Adatszerkezetek” tantárgy , 1. félév 2. előadás’2009 (vázlat) 1

1. Modulteszt 1

2. A Tömb típuskonstrukció. 4

2.1. A tömb algebrai specifikációja. 4

2.2. A tömb algoritmikus specifikációja. 5

2.2.1. A tömb exportmoduljai 5

2.2.2. A tömb reprezentációs-implementációs modulja. 8

2.3. Speciális tömbök. 16

2.3.1. A „specialitás” mibenlétéről 16

2.3.2. Szisztematikusan elhelyezkedő elemek tömbökben. 16

2.3.3. Hiányosan kitöltött tömbök. 17

2.3.4. Generálható elemek tömbökben. 18

Tartalom.. 20

---

[1] A fájlba nyomtatás akkor célszerű, ha a tesztelés eredményét dokumentálnunk is kell.

[2] A CrLf globális konstans ’#10#13’ értékkel.

[3] Esetleg: NemDef, ha az Elem típusban nem létezik a konstrukciós Létrehoz_e művelet.

[4] Szokásos elvárásokkal; pl. Sorszám(Min’TElem)=0.

[5] Az Ef 2. tényezőjét egyszerűbben is írhatnánk: "iÎTIndex: Be(t(1)).Ef. Miért?

[6] L. az inicializálásnál!

[7] Ez sem igaz a Pascal esetében!