ProgramozásMódszertan
3. előadás’2004
(vázlat)

1.      Pascal kódolási szabályok

1.1. Miről is van szó?

·        A kódolás minél mechanikusabbá tétele.

·        Csak a nyelv meghatározta dolgokra koncentrálás. Gondoljunk a ’Be:… [..]’ szerkezet­re, amelyet egészen más hozzáállással kell kódolni pl. Turbo Pascal-ban, mint a Delphi-ben.

·        „Csak” a felhasználóval való zavartalan kommunikáció megszervezése.

Megjegyzés: a programok legtöbbjénél ez viszi el a kód 95%-át (bár nem biztos, hogy a kódolási idő 95%-át). Tehát nem arról van szó, hogy bagatellizálni kell e programozási lépést, hanem csak azt, hogy a feladat lényegét nem a kódolás során kell megoldani (hanem előbb).

·        A kódolási szabályok az adott programozási nyelven nyugszanak, tehát egyediek.

1.2. A Turbo Pascal kódolási szabályok

Az alábbiakban nem törekszünk teljességre. A lényeg és az „izgalmasabb” részletek bemu­tatása a cél. S mintául szolgáljanak más programozási nyelvek kódolási szabályainak meg­tervezéséhez.

Algoritmikus szerkezet

(Turbo) Pascal-szerkezet
Típusdefiníció

Konstans
  MaxN:Egész(100)
Típus
  TMag=Tömb(1..MaxN:TElem)
  TDátum=Rekord(év,hó,nap:Egész)

Const
  MaxN=100;
Type
  TMag=Array[1..MaxN] of TElem;
  TDatum=Record
           ev,ho,nap:Word
         End;
Típusdeklaráció

Változó
  N,i:Egész
Konstans
  ma:TDátum(év:2001,hó:10,nap:1)
  mag:TMag

Var
  N,i:Integer;
Const
  ma:TDatum=(ev:2001;ho:10;nap:1);
  mag:TMag;
Értékadás

x:=kif

x:=kif;
Alprogramhívás

Beolvasás(N,mag)

Beolvasas(N,mag);
Adatbeolvasás

Be: N [0£N£MaxN]






Be: mag(1..N) [mag(1)>0 és
               mag(2..N-1)³0 és
               mag(N)>0]

Repeat
 {$i-}
 Write(’Mi a szösz:’);
 Readln(N);
 {$i+}
Until (IOResult=0) and
      (N>=0) and (N<=MaxN);

Writeln(’Mi a szösz tömb ez?’);
Repeat
 {$i-}
  Write(1:3,’. elem:’);
  Readln(mag[1]);
 {$i+}
Until (IOResult=0) and
       (mag[1]>0);
For i:=2 to N-1 do
Begin
 Repeat
  {$i-}
  Write(i:3,’. elem:’);
  Readln(mag[i]);
  {$i+}
Until (IOResult=0) and
       (mag[i]>=0);
End;{For i}
Repeat
 {$i-}
  Write(N:3,’. elem:’);
  Readln(mag[N]);
 {$i+}
Until (IOResult=0) and
       (mag[N]>0);
…

…

…

2.      Specifikáció – Algoritmus – Kód

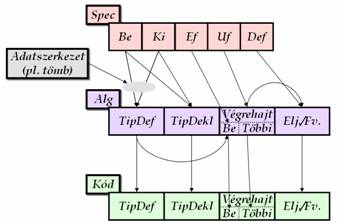
2.1. Kapcsolatok

[ Adatszerkezet Þ Alg.TipDef ]

Spec.Be + Spec.Ki Þ Alg.TipDef Þ Kód.TipDef
Spec.Be + Spec.Ki + Alg.TipDef Þ Alg.TipDekl Þ Kód.TipDekl

Spec.Ef Þ Alg.Be Þ Kód.Beolv

Spec.Uf Þ Alg.Végrehajt [Þ Kód.Elj/Fv[1]] Þ Kód.Végrehajt [Þ Kód.Elj/Fv]

Spec.Def Þ Alg.Elj/Fv Þ Kód.Elj/Fv

1. ábra. Specifikáció – Algoritmus – Kód.

2.2. Egy korábbi feladatpélda:

Specifikáció:

Be:   NÎN, HallgatókÎ(Név´Szak´Évfolyam)*,
Név=S, Szak={Info, Mat, Fiz, …[2]}, Évfolyam=N

Ki:    VaneÎL

Ef:    Hossz(Hallgatók)=N Ù
"iÎ[1..N]: Hallgatóki.Név¹’’ Ù Hallgatóki.ÉvfolyamÎ[1..5]

Uf:    Vane = $iÎ[1..N]: Hallgatóki.Szak=Info Ù Hallgatóki.Évfolyam=1

Adatszerkezet: Tömb Þ Alg.TipDef :

Konstans MaxN:Egész(100)

Spec.Be + Spec.Ki Þ Alg.TipDef :

Típus   TNév=Szöveg
        TSzak=(Info, Mat, Fiz, …)
        TÉvfolyam=Egész
        THallgató:Rekord(
                    Név:TNév
                    Szak:TSzak
                    Évfolyam:TÉvfolyam)
        THallgatók=Tömb(1..MaxN:THallgató)

Spec.Be + Spec.Ki + Alg.TipDef Þ Alg.TipDekl :

Változó N:Egész
        Hallgatók:THallgatók
        Vane:Logikai

Spec.Ef Þ Alg.Be Þ Kód.Beolv

Be: N [0£N£MaxN]
Be: Hallgató(1..N)
 [Hallgató(1..N).Név¹’’ és
  Hallgató(1..N).ÉvfolyamÎ[1..5]]

l. előbb

Spec.Uf Þ Alg.Végrehajt Þ Kód.Végrehajt

…

3.      Mit jelent a tételbizonyítás

Figyeljük meg például a Kiválasztás tétel bizonyítását!

Specifikáció:

Be:    NÎN , XÎH*, T:H®L

Ki:    SorszÎN

Ef:     Hossz(X)=N Ù $iÎ[1..N]: T(xi)

Uf:    SorszÎ[1..N]  Ù  T(xSorsz)

Alg:

Konstans MaxN:Egész(???)
Típus THk=Tömb(1..MaxN:TH)

Eljárás Kiválasztás(Konstans N:Egész, X:THk
                    Változó  Sorsz:Egész):
  Változó
    i:Egész

  i:=1
  Ciklus amíg nem T(X(i))
    i:+1
  Ciklus vége
  Sorsz:=i
Eljárás vége.

3.1. A bizonyítás ötlete

A helyes program mint állapottér-transzformáció az Ef által behatárolt részállapotból indul ki, és utasításról utasításra haladva transzformálja az állapottér egyes komponenseit mind­addig, amíg az Uf által meghatározott végállapotba nem jut.

Kövessük tehát mi is utasításról utasításra az állapottér transzformált részállapot-halmazait! Vagyis adjuk meg a predikátumokat az egyes utasítások mögött kiindulva az Ef-ből. Ha elju­tottunk az Uf-be, akkor a bizonyítás kész.

3.2. Az „egyenes” bizonyítás lehetetlensége

1.      Egy feladat specifikációjában az Ef-t tetszőlegesen szűkíthetjük, a korábbi megoldás meg­oldás marad ezután is.

Például, Ef: … $iÎ[1..N Div 2] : T(x2*i) – azaz létezik páros indexű T-tulajdonságú

2.      Az Ef-nek vajmi kevés közölni valója van a feladatról. Már csak azért is igaz ez a ki­jelentés, mert a tételek között soknak ugyanaz (pl. AZONOSAN IGAZ) az Ef-e.

3.3. Kiindulópont

A legtöbb támpontot a feladatról az Uf ad. Ebből kell tehát kiindulni, s követni visszafelé a „transzformáció-inverzének” a működését, amíg az Ef-hez el nem érünk.

A transzformáció utáni állapotból az utasítás előttire következtetni nem mindig könnyű, ezért segédállításokat (és rajtuk nyugvó következtetési szabályokat) kell találni.

Az elméleti részletek mellőzésével élvezzük a levezetés báját, lényegét.

3.4. Menet

Az algoritmus tevékenység részére kell figyelnünk csak. Megfelelő helyekre illesztünk be ál­lításokat. Az állítások paraméterfüggését korlátozzuk a legjellegzetesebb adatra. Pl. az X tömbtől való függést, mint nyilvánvalót, nem jelöljük.

2. ábra. A bizonyítás vázlata.

 

0.

[f4]
 i:=1
[f3(i)]
 Ciklus [f2(i)] amíg nem T(X(i))
   i:+1
 Ciklus vége
[f1(i)]
 Sorsz:=i
[Uf(Sorsz)]

Uf(Sorsz): SorszÎ[1..N]  Ù  T(xSorsz)

1.

[f4]
 i:=1
[f3(i)]
 Ciklus [f2(i)] amíg nem T(X(i))
   i:+1
 Ciklus vége
[f1(i)]
 Sorsz:=i
[SorszÎ[1..N]  Ù  T(xSorsz)]

1. állítás: ha Uf(Sorsz) igaz a ’Sorsz:=i’ után, akkor előtte igaz kell legyen:
f1(i): iÎ[1..N]  Ù  T(xi).

Ui.: helyettesítsük be i-t Uf-ben a Sorsz he­lyére! Mivel Uf(Sorsz) igaz, és a ’Sorsz:=i’ után épp i értékét örökli, így nyilvánvaló: Uf(i)=Igaz. Azaz helyes:
f1(i)◄Sorsz:=i►Uf(Sorsz) [3] [4]                  à

2.

[f4]
 i:=1
[f3(i)]
 Ciklus [f2(i)] amíg nem T(X(i))
   i:+1
 Ciklus vége
[iÎ[1..N]  Ù  T(xi)]
 Sorsz:=i
[SorszÎ[1..N]  Ù  T(xSorsz)]

f2(i): "jÎ[1..i-1]: ØT(xj)

2. állítás: ha f2 egyszer igaz, akkor a ciklus egyszeri végrehajtása után is igaz marad.

Ui.: Kövessük a ciklus egyszeri végrehajtá­sát; hogy a ciklusmag végrehajtódjék, kell, hogy ØT(X(i))ºIgaz teljesüljön. Azaz

     f2(i) ÙØT(xi)◄i:+1►f2(i-1) Ù ØT(xi-1)º
      ("jÎ[1..i-2]: ØT(xj)) Ù ØT(xi-1)ºf2(i)    à

3. állítás: f2(1) igaz, azaz a 2. állítás feltétele tud teljesülni.

Ui.: f2(1) º"jÎ[1..1-1]: ØT(xj)ºIgaz           à

4. állítás: Ef Ù f2(i) Ù Ø(ØT(xi)) Þ f1(i); itt a ’ØT(xi)’ a ciklusfeltétel.

Ui.: Ef Ù f2(i) Ù Ø(ØT(xi)) º
      $iiÎ[1..N]: T(xii) Ù
        ("jÎ[1..i-1]: ØT(xj)) Ù T(xi)º
      [ii=i Ù] iÎ[1..N] Ù T(xi)                         à

Az Ef-ből kihagytuk az ’N=Hossz(X)’ felté­telrészt, ami a lényeget nem befolyásolja.

Következmény: f2 ún. invariáns állítás.

(Ui.: 2.,3. és 4. állítás következménye.)

3.

[f4]
 i:=1
[f3(i)]
 Ciklus ["jÎ[1..i-1]: ØT(xj)]
        amíg nem T(X(i))
   i:+1
 Ciklus vége
[iÎ[1..N]  Ù  T(xi)]
 Sorsz:=i
[SorszÎ[1..N]  Ù  T(xSorsz)]

f3(i): Ef Ù i=1

5. állítás: ha Ef Ù i=1 Þ (f3(i)Þf2(i)).

Ui.: Nyilvánvaló, hogy Ef Þ f3(1)ºIgaz
     és a 3. állítás szerint: f2(1)ºIgaz                 à

4.

[f4]
 i:=1
[Ef Ù i=1]
 Ciklus ["jÎ[1..i-1]: ØT(xj)]
        amíg nem T(X(i))
   i:+1
 Ciklus vége
[iÎ[1..N]  Ù  T(xi)]
 Sorsz:=i
[SorszÎ[1..N]  Ù  T(xSorsz)]

f4: Ef

6. állítás: f4 választása helyes.

Ui.: f4ºEf◄i:=1►Ef Ù i=1ºf3(i)                 à

5.

[Ef]
 i:=1
[Ef Ù i=1]
 Ciklus ["jÎ[1..i-1]: ØT(xj)]
        amíg nem T(X(i))
   i:+1
 Ciklus vége
[iÎ[1..N]  Ù  T(xi)]
 Sorsz:=i
[SorszÎ[1..N]  Ù  T(xSorsz)]

 

Figyeljük meg, mi történik, ha az Ef nem teljesül a bemenő adatra! Válasz: a ciklusból nincs (legális) „menekvés”! Vagyis, amit kaptunk így fogalmazható meg: ha a program terminál (megáll, eljut egy „legális” végállapotba), akkor az Uf-nek megfelelő állapotban lesz.

Koncentráljunk mármost a legális megállásra! A megállásnak az a feltétele, hogy legyen olyan („absztrakt”) N-értékű függvény, amivel a még hátralévő ciklus lépések számát le tud­juk írni, s igaz rá, hogy a ciklus minden lépése során határozottan csökken.

[f4]
 i:=1
[f3(i)]
 Ciklus [f2(i) Ù cl(i)>0]
        amíg nem T(X(i))
   i:+1
 Ciklus vége
[iÎ[1..N]  Ù  T(xi)]
 Sorsz:=i
[SorszÎ[1..N]  Ù  T(xSorsz)]

Az f2-t, f3-at és f4-et nem részleteztük, cl a még hátralévő cikluslépések számát leíró függvény (F(N,N)).

cl(i): K–i (ahol KÎN rögzített konstans)

7. állítás:  $jÎ[1..N]: T(xj) Þ
      $KÎ[1..N]: "iÎ[1..K): cl(i)>cl(i+1) Ù
      cl(K)=0. [5]

Ui.: Legyen K:
   KÎ[1..N]: T(xK) Ù "jÎ[1..K-1]: ØT(xK).

   Ekkor "jÎ[1..K-1]: cl(j)>0 Ù cl(K)=0     à

Tehát:

f3(i): $jÎ[1..N]: T(xj) Ù i=1,

         röviden szólva: Ef Ù i=1

[f4]
 i:=1
[$jÎ[1..N]: T(xj)  Ù  i=1]
 Ciklus [f2(i) Ù K-i>0]
        amíg nem T(X(i))
   i:+1
 Ciklus vége
[iÎ[1..N]  Ù  T(xi)]
 Sorsz:=i
[SorszÎ[1..N]  Ù  T(xSorsz)]

f4: $jÎ[1..N]:T(xj), azaz Ef

Állítás: f4◄i:=1►f3(1)

Ui.: nyilvánvaló.

4.      További egyszerűbb Programozási tételek

4.1. Megszámolás tétel

Megszámolás(H*,F(H,L)):N

Be:    NÎN , XÎH*, T:H®L

Ki:     DbÎN

Ef:     Hossz(X)=N

Uf:   

Def:  :L®{0,1}
          

Alg:

Konstans MaxN:Egész(???)
Típus THk=Tömb(1..MaxN:TH)

Eljárás Megszamolás(Konstans N:Egész, X:THk
                    Változó  Db:Egész):
  Változó
    i:Egész

  Db:=0
  Ciklus i=1-től N-ig
    Ha T(X(i)) akkor Db:+1
  Ciklus vége
Eljárás vége.

Megjegyzések:

1.      Az itt felvetődő „elemszámlálásos” ötlet és formalizmus sokszor felhasználandó! A továbbiakban nem definiáljuk a khi-függvényt.

2.      Érdemes eltűnődni a tételnek és a sorozatszámítás tétel (S-s változatának) nagyfokú hasonlóságán.

4.2. Maximumkiválasztás tétel

Maximumkiválasztás(H*,F(HxH,L)):N [6]  vagy  Maximumkiválasztás(H*,F(HxH,L)):H[7]

Be:    NÎN , XÎH*, £ÎF(HxH,L)

Ki:    MaxiÎN

Ef:     Hossz(X)=N Ù N³1 Ù RendezettHalmaz£(H)

Uf:    MaxiÎ[1..N]  Ù  "iÎ[1..N] : xMaxi³xi

Alg:

Konstans MaxN:Egész(???)
Típus THk=Tömb(1..MaxN:TH)

Eljárás Maximumkiválasztás(Konstans N:Egész, X:THk
                           Változó  Maxi:Egész):
  Változó
    i:Egész

  Maxi:=1
  Ciklus i=2-től N-ig
    Ha X(i)>X(Maxi) akkor Maxi:=i
  Ciklus vége
Eljárás vége.

Megjegyzések:

1.      Az algoritmusbeli >-reláció a specifikációbeli £ „értelemszerű” algoritmikus párja.

2.      Meggondolandó, milyen specifikációra „rimmelne” az az algoritmus, amelyben a > helyett ³-reláció szerepelne!

3.      Specifikálja a maximumkiválasztás másik változatát is!

4.3. Kiválogatás tétel

Kiválogatás(H*,F(H,L)):N* [8]   vagy  Kiválogatás (H*,H,F(H,L)):H* [9]

Be:    NÎN , XÎH*, T:H®L

Ki:    DbÎN , YÎN*

Ef:     Hossz(X)=N

Uf:     Ù YÎ[1..N]Db  Ù  "iÎ[1..Db]: T(xyi)  Ù  HalmazFölsorolás(Y)

Alg:

Konstans MaxN:Egész(???)
Típus THk=Tömb(1..MaxN:TH)
      TIndk=Tömb(1..MaxN:Egész)

Eljárás Kiválogatás(Konstans N:Egész, X:THk
                    Változó  Db:Egész, Y:TIndk):
  Változó
    i:Egész

  Db:=0
  Ciklus i:=1-től N-ig
    Ha T(X(i)) akkor Db:+1; Y(Db):=i
  Ciklus vége
Eljárás vége.

 

Tartalom

ProgramozásMódszertan 3. előadás’2004 (vázlat) 1

1.     Pascal kódolási szabályok. 1

1.1. Miről is van szó?. 1

1.2. A Turbo Pascal kódolási szabályok. 1

2.     Specifikáció – Algoritmus – Kód. 2

2.1. Kapcsolatok. 2

2.2. Egy korábbi feladatpélda: 3

3.     Mit jelent a tételbizonyítás. 4

3.1. A bizonyítás ötlete. 4

3.2. Az „egyenes” bizonyítás lehetetlensége. 4

3.3. Kiindulópont 5

3.4. Menet 5

4.     További egyszerűbb Programozási tételek. 8

4.1. Megszámolás tétel 8

4.2. Maximumkiválasztás tétel 8

4.3. Kiválogatás tétel 9

Tartalom.. 10

 


[1] Ti. a finomítások eljárásai, függvényei.

[2] A „…” jelentése: itt egy felsorolás lenne, amit most nem folytatunk) formálisan persze kellene, mivel ki nem található)! Figyelem: így csak egy-szak rendelhető a hallgatóhoz! Nagy baj ez?

[3] A „p1◄u►p2” jelentése: „a p1–ből az u utasítás végrehajtása után igaz p2”.

[4] Általában is igaz, hogy „P(f(x))◄y:=f(x)►P(y)”. Ezt hívják Hoare rendszerében értékadási axiómának.

[5] Az ilyen függvényt nevezik variáns függvénynek.

[6] Maximális elem indexének kiválasztása.

[7] Maximális elem (értékének) kiválasztása.

[8] A T-tulajdonságúak indexeinek kiválogatása.

[9] A T-tulajdonságúak (értékeinek) kiválogatása. Uf: Db=… Ù YÎHN Ù "iÎ… Ù YÍX