ProgramozásMódszertan
5. előadás’2004
(vázlat)

1. Rendezési tételek

1.1. Rendezési tételekről előzetesen

1.1.1. A feladat

Egy adatsorozat elemeinek átrendezése úgy, hogy elemei a művelet után valamely „szempontból” rendezettek legyenek.

A szempontot gyakorta az elem egy valamely része, mezője testesíti meg: a kulcs.

Azaz az Elem=Kulcs´Érték. Ekkor e₁£e₂ e₁.Kulcs£e₂.Kulcs.

E helyett elképzelhető egy, az elemek alaphalmazán értelmezett olyan függvény is, amely értékkészlete egy nyilvánvalóan rendezett halmaz, pl. N.

Azaz KulcsFv:Elem®N[1]. Ekkor e₁£e₂ KulcsFv(e₁)£ KulcsFv(e₂)

1.1.2. Fajtái

· Belső rendezések – a rendezendő sorozat befér a memóriába, ezért feltehetjük, hogy tömbben tárolható.

· Külső rendezések – a sorozat egésze nem tartható egyidejűleg a tárban, ekkor elemei valamely (háttértár) állomány(ok)ban tárolódnak. (L. Adatfeldolgozás előadásban.)

Megjegyzés:

Ha –bár nem fér a sorozat a memóriába, de– olyan háttértár adatszerkezetben tárolódik, amely közvetlen elérésű, vagyis létezik egy rajta értelmezett indexszelés-szerű művelet (az elemeléréshez, illetve az elemmódosításhoz), akkor kicsi átalakítással a belső rendezés algoritmusai alkalmazhatók.

Ebből a megjegyzésből is érződik a fenti fajták elnevezésének nem túl szerencsés volta. Kifejezőbb lenne valami efféle: „Rendezés közvetlen elérésű adatszerkezetben”, ill. „Rendezés szekvenciális adatszerkezetben”.

1.1.3. Algoritmikus „filozófiák”

Mivel a rendezés során permutáljuk a bemenő sorozatot, sok út vezet a rendezettből rendezett felé, ezért sokféle módszer található a permutálásra. Ezek eltérő hatékonysággal rendelkeznek, más körülmények között másképpen („okosan”, „bután”) viselkednek.

Fajta	Lényeg
Transzpozíciós	Ha az összehasonlításban szereplő elempárok egymáshoz képesti sorrendje (transzpozíció) rossz, akkor megcseréljük… Pl.: (4,3,2,5,1) Þ (3,4,2,5,1) Þ (3,2,4,5,1) Þ (3,2,4,5,1) Þ (3,2,4,1,5) Þ (2,3,4,1,5) Þ (2,3,4,1,5) Þ (2,3,1,4,5) Þ …
Szelekciós	Mindig a rendezettségszerinti következő kiválasztása (szelekciója), majd helyre tétele csere útján… Pl.: (4,3,2,5,1) Þ …minimum kiválasztás(4,3,2,5,1): 1 … Þ (1,3,2,5,4) Þ …minimum kiválasztás(3,2,5,4): 2 … Þ (1,2, 3,5,4) Þ …
Beszúrásos	A következő elemnek a rendezettségnek megfelelő helyre tétele a már rendezett részsorozatban… Pl.: (4,3,2,5,1) Þ (3,4,2,5,1) Þ (2,3,4,5,1) Þ (2,3,4,5,1) Þ (1,2,3,4,5)

1.1.4. A hatékonyságról dióhéjban

Mit mérhetünk?	Hogyan mérhetünk?
· Helyfoglalás	· Absztrakt módon
· Végrehajtási idő	Elem-hasonlítások száma (£H)
A mérés „skálája”:	Elem-mozgatások száma (:=H)
· Minimális – optimista	Elemek össz-száma
· Átlagos – praktikus	· „Colstockkal-stopperrel”
· Maximális – pesszimista

Az absztrakt mérés matematikai eszközeiről:[2]

Miként változik az elemszámmal (sorozathosszal) a hasonlításszám, ill. a mozgatásszám; társzükséglet aszimptotikusan?

Egy N®N függvény aszimptotikus[3] viselkedésének kifejezésére (többek közt) a Q- (theta), O- (nagy ordó), W-függvények alkalmasak:

Q(g(n)):={f(n) ½ $c₁,c₂ÎR₊, n₀ÎN: "n³n₀ Þ c₁*g(n)£f(n)£c₂*g(n) } – korlátos

O(g(n)):={f(n) ½ $cÎR₊, n₀ÎN: "n³n₀ Þ 0£f(n)£c*g(n) } – felülről korlátos

W(g(n)):={f(n) ½ $cÎR₊, n₀ÎN: "n³n₀ Þ c*g(n)£f(n) } – alulról korlátos

Megjegyzések:

1. f(n)=O(g(n)) helytelen szokás, hisz O(…) függvényhalmaz. Helyesen: f(n)ÎO(g(n))

2. Értelme persze csak akkor van a fentieknek, ha az f(n) függvény valamilyen „egyszerű” függvény; pl. hatványfüggvény, exponenciális függvény stb.

Pl.: ha f(n)=A*n^2+B*n+C, akkor fÎO(n^2), hiszen c:=2*A, s ekkor megadható egy megfelelő választás n0-ra hogy n³n0 esetén 0£f(n)£c*n^2 teljesüljön. Sőt az fÎQ(n^2) is igaz.

1.1.5. A specifikációjukról

Legtöbbjük specifikációja ugyanaz:

BelsőRendezés(H^*,F(H´H,L)):H^*	Megjegyzések:
Be: NÎN, XÎH^*, H=Kulcs´Érték, £Kulcs:Kulcs´Kulcs®L	Sorozat és egy reláció.
Ki: X’ÎH^*	A transzformáció helyben történik.
Ef: N=Hossz(X) Ù £Kulcs rendezés Ù X közvetlen elérésű	Rendezési reláció a szokásos tulajdonságokkal; X elemei indexeléssel elérhetők: $ Elem(x,i)=xi operáció….
Uf: X’ÎP(X) Ù RendezettSorozat£(X’)	A kimenet a bemenet egy permutációja, amelyben az elemek rendezetten követik egymást. A továbbiakban is föltesszük, hogy a rendezettség mindig nem-csökkenőt jelent.

A tételek szerkezete visszatérő:

· specifikáció (amit elhagyunk, ha a fentivel megegyező),

· algoritmus, amelyben az alábbi definíciós rész unós untig ismétlődik (ezért ezt sem írjuk le):

Konstans MaxN:Egész(???)
Típus THk=Tömb(1..MaxN:TH) [TH az alaphalmaz típusa]

Infix Operátor £(Konstans e,f:TH):Logikai
Másként KisebbEgyenlő
KisebbEgyenlő:=e.Kulcs£f.Kulcs [visszavezetés £Kulcs-ra]
Operátor vége.

Infix Operátor >(Konstans e,f:TH):Logikai
Másként Nagyobb
Nagyobb:=nem(e£f)
Operátor vége.

· hatékonysági megfontolások.

1.2. Belső rendezések

1.2.1. Egyszerű cserés rendezés

CsereRendezés(H^*,F(H´H,L)):H^*

Alg:

Eljárás CsereRendezés(Konstans N:Egész, Változó[4] X:THk):
Változó i,j:Egész

Ciklus i=1-től N-1-ig
Ciklus j=i+1-től N-ig
Ha X(i)>X(j) akkor Csere(X(i),X(j))
Ciklus vége
Ciklus vége
Eljárás vége.

Eljárás Csere(Változó e,f:TH):[5]
Változó s:TH

s:=e; e:=f; f:=s
Eljárás vége.

A filozófiát tekintve: transzpozíciós rendezés.

Hatékonyság:

Szempont	Min	Max
Helyfoglalás	N+1[6]		Q(N)
Hasonlításszám	N*(N-1)/2		Q(N^2)
Mozgatásszám	0	3*N*(N-1)/2	O(N^2)

Érdemes megfontolni: milyen tulajdonságú bemenő adat esetén viselkedik a fentiek szerint.

1.2.2. Minimumkiválasztásos rendezés

Minimumkiálasztásos(H^*,F(H´H,L)):H^*

Alg:

Eljárás MinimumKiválasztásos(Konstans N:Egész
Változó X:THk):
Változó i,j:Egész

Ciklus i=1-től N-1-ig
[mini:=MinimumKiválasztás(X(i..N),>)]
mini:=i
Ciklus j=i+1-től N-ig
Ha X(mini)>X(j) akkor mini:=j
Ciklus vége
Csere(X(i),X(mini))
Ciklus vége
Eljárás vége.

A filozófiát tekintve: szelekciós rendezés.

Hatékonyság:

Szempont	Min	Max
Helyfoglalás	N+1		Q(N)
Hasonlításszám	N*(N-1)/2		Q(N^2)
Mozgatásszám	3*(N-1)		Q(N)

Gondoljon bele: mi lehet az invariáns állítás az egyes ciklusokban az egyszerű cserés és mi ennél a rendezésnél?

1.2.3. Buborékos rendezés

Buborékos(H^*,F(H´H,L)):H^*

Alg:

Eljárás Buborékos(Konstans N:Egész, Változó X:THk):
Változó i,j:Egész

Ciklus i=N-től 2-ig –1-esével
Ciklus j=1-től i-1-ig
Ha X(j)>X(j+1) akkor Csere(X(j),X(j+1))
Ciklus vége
Ciklus vége
Eljárás vége.

A filozófiát tekintve: transzpozíciós rendezés.

Hatékonyság:

Szempont	Min	Max
Helyfoglalás	N+1		Q(N)
Hasonlításszám	N*(N-1)/2		Q(N^2)
Mozgatásszám	0	3*N*(N-1)/2	O(N^2)

Észreveheti, hatékonysági szempontból megegyezik az egyszerű cserés rendezéssel. Meglepő ez?

1.2.4. Javított buborékos rendezés

JavítottBuborékos(H^*,F(H´H,L)):H^*

Alg:

Eljárás JavítottBuborékos(Konstans N:Egész
Változó X:THk):
Változó i,j,csH:Egész [csH:a csere helye, indexe]

i:=N
Ciklus amíg i³2
csH:=0
Ciklus j=1-től i-1-ig
Ha X(j)>X(j+1) akkor Csere(X(j),X(j+1)); csH:=j
Ciklus vége
i:=csH
Ciklus vége
Eljárás vége.

A filozófiát tekintve: transzpozíciós rendezés.

A csH kezdőértékére tud-e még más, többé-kevésbé „logikus” választást?

Hatékonyság:

Szempont	Min	Max
Helyfoglalás	N+1			Q(N)
Hasonlításszám	N-1		N*(N-1)/2	W(N), O(N^2)
Mozgatásszám	0		3*N*(N-1)/2	O(N^2)

A hatékonyság „átlagos” esetben javul.

1.2.5. Beillesztéses rendezés

Beillesztéses(H^*,F(H´H,L)):H^*

Alg:

Eljárás Beillesztéses(Konstans N:Egész, Változó X:THk):
Változó i,j:Egész

Ciklus i=2-től N-ig
j:=i-1
Ciklus amíg j³1 és X(j)>X(j+1)
Csere(X(j),X(j+1)); j:-1
Ciklus vége
Ciklus vége
Eljárás vége.

A filozófiát tekintve: beszúrásos rendezés.

Hatékonyság:

Szempont	Min	Max
Helyfoglalás	N+1			Q(N)
Hasonlításszám	N-1		N*(N-1)/2	W(N), O(N^2)
Mozgatásszám	0		3*N*(N-1)/2	O(N^2)

Gondoljon bele: mik az invariáns állítások ennél a rendezésnél?

1.2.6. Javított beillesztéses rendezés

JavítottBeillesztéses(H^*,F(H´H,L)):H^*

Alg:

Eljárás JavítottBeillesztéses(Konstans N:Egész
Változó X:THk):
Változó i,j:Egész
segéd:TH

Ciklus i=2-től N-ig
j:=i-1; segéd:=X(i)
Ciklus amíg j³1 és X(j)>segéd
X(j+1):=X(j); j:-1
Ciklus vége
X(j+1):=segéd
Ciklus vége
Eljárás vége.

A filozófiát tekintve: beszúrásos rendezés.

Hatékonyság:

Szempont	Min	Max
Helyfoglalás	N+1			Q(N)
Hasonlításszám	N-1		N*(N-1)/2	W(N), O(N^2)
Mozgatásszám	2*(N-1)		2*(N-1)+N*(N-1)/2	W(N), O(N^2)

1.3. Speciális rendezések

1.3.1. Szétosztó rendezés

Egy nem helyben dolgozó rendezés, amely igen kemény elvárásokat fogalmaz meg a bemenő sorozatra.

SzétosztóRendezés((Kulcs´H)^*,F(Kulcs´Kulcs,L)): (Kulcs´H)^*

Be: NÎN, XÎ(Kulcs´H)^*,Kulcs=N , £Kulcs:Kulcs´Kulcs®L – £Kulcs elhagyható, hisz létezése nyilvánvaló

Ki: YÎ(Kulcs´H)^* – nem helyben rendezés

Ef: N=Hossz(X) Ù £Kulcs rendezés Ù X.KulcsÎP((1..N)) – £Kulcs elhagyható, hisz tulajdonsága nyilvánvaló

Uf: YÎP(X) Ù RendezettSorozat_£(Y)

Alg:

Eljárás SzétosztóRendezés(Konstans N:Egész, X:THk
Változó Y:THk):
Változó
i,j:Egész

Ciklus i=1-től N-ig
Y(X(i).Kulcs):=X(i)
Ciklus vége
Eljárás vége.

Hatékonyság:

Szempont	Min	Max
Helyfoglalás	2*N		Q(N)
Hasonlításszám	0		O(1)
Mozgatásszám	N		Q(N)

1.3.2. Számlálva szétosztó rendezés

Az előbbi rendezéstől abban tér el, hogy gyengíti az előfeltételt, és a tényleges rendezés előtt némi –kényszerű– előkészületeket tesz.

SzámlálvaSzétosztóRendezés((Kulcs´H)^*,F(Kulcs´Kulcs,L)): (Kulcs´H)^*

Be: NÎN , XÎ(Kulcs´H)^*, MÎN , Kulcs=N [£Kulcs:Kulcs´Kulcs®L]

Ki: YÎ(Kulcs´H)^*

Ef: N=Hossz(X) Ù "iÎ[1..N]: x_i.KulcsÎ{1..M} [Ù £Kulcs rendezés]

Uf: YÎP(X) Ù RendezettSorozat_£(Y)

Alg:

Eljárás SzámlálvaSzétosztóRendezés(Konstans N:Egész, X:THk
Változó Y:THk):
Konstans
MaxM:Egész(???)
Változó
i:Egész
Db:Tömb(1..MaxM:Egész)

Db(1..M):=0
Ciklus i=1-től N-ig
Db(X(i).Kulcs):+1
Ciklus vége
Ciklus i=2-től M-ig
Db(i):+Db(i-1) [Db(i): i. kulcsúak utolsójára mutat]
Ciklus vége
Ciklus i=1-től N-ig
Y(Db(X(i).Kulcs)):=X(i); Db(X(i).Kulcs):-1
Ciklus vége
Eljárás vége.

Érdemes eltöprengeni, mely tételek bukkantak föl az algoritmusban!

Hatékonyság:

Szempont	Min	Max
Helyfoglalás	2*N+e*M		Q(N)
Hasonlításszám	0		Q(1)
Mozgatásszám	N		Q(N)
Kulcsmező indexelés száma	3*N §		Q(N)

A számláló tömb elemének mérete kicsiny, azaz „epszilon” (lehet) a rendezendő sorozat eleméhez képest. Mivel számosan lehetnek, helyet mégis foglalnak.

1.3.3. Számláló rendezés

Az alábbi rendezés sem helyben rendez, és több rendezésből is átvesz ötleteket.

SzámlálóRendezés(H^*,F(H´H,L)):H^*

Be: NÎN, XÎH^*, £:H´H®L

Ki: YÎH^*

Ef: N=Hossz(X) Ù £_H rendezés

Uf: YÎP(X) Ù RendezettSorozat_£(Y)

Alg:

Eljárás SzámlálóRendezés(Konstans N:Egész, X:THk
Változó Y:THk):
Változó
i,j:Egész
Db:Tömb(1..MaxN:Egész)

Db(1..N):=1

[Majdnem egyszerű cserés rendezés:]
Ciklus i=1-től N-1-ig
Ciklus j=i+1-től N-ig
Ha X(i)>X(j) akkor Db(i):+1
különben Db(j):+1
Ciklus vége
Ciklus vége

[Szétosztó rendezés:]
Ciklus i=1-től N-ig
Y(Db(i)):=X(i)
Ciklus vége
Eljárás vége.

Az egyszerű cserés rendezést csak az inverziók felderítésére használjuk, az elemmozgatást a végére hagyjuk. Hogy miért?

Hatékonyság:

Szempont	Min	Max
Helyfoglalás	2*N+e*N		Q(N)
Hasonlításszám	N*(N-1)/2		Q(N^2)
Mozgatásszám	N		Q(N)
Kulcsmező indexelés száma	N		Q(N)

1.4. Shell rendezés

Egy valóban hatékony rendezéssel fejezzük be a rendező algoritmusok sorát.

ShellRendezés(H^*,F(H´H,L)):H^*

Kezdjük egy beszúrásos rendezéses példával! A példa egy-egy sora a belső ciklus teljes lefutása utáni állapotot rögzíti. Ahol mozgás volt ott színes a háttér.

503	87	512	61	908	170	897	275	653	426	154	509	612	677	765	703
87	503	512	61	908	170	897	275	653	426	154	509	612	677	765	703
87	503	512	61	908	170	897	275	653	426	154	509	612	677	765	703
61	87	503	512	908	170	897	275	653	426	154	509	612	677	765	703
61	87	503	512	908	170	897	275	653	426	154	509	612	677	765	703
61	87	170	503	512	908	897	275	653	426	154	509	612	677	765	703
61	87	170	503	512	897	908	275	653	426	154	509	612	677	765	703
61	87	170	275	503	512	897	908	653	426	154	509	612	677	765	703
61	87	170	275	503	512	653	897	908	426	154	509	612	677	765	703
61	87	170	275	426	503	512	653	897	908	154	509	612	677	765	703
…
61	87	154	170	275	426	503	509	512	612	653	677	703	765	897	908

Megállapítható, hogy nagyon lassan haladnak, nagyon sok apró lépéssel araszolnak a magas értékek a helyük felé. Ebből támadhat az ötlet: ne „egyesével” tekintsük sorozatnak a rendezendőt, hanem nagyobb „lépésközösével”. Pontosabban több részsorozatot rendezzünk egyidejűleg, s „maj’mekláttyuk”… Nézzük pl. az előbbit 7-esével bontva részsorozatokra. Most az egy részsorozatba tartozókat azonos színű számokkal jelöltük.

1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16
503	87	512	61	908	170	897	275	653	426	154	509	612	677	765	703
275	87	426	61	509	170	677	503	653	512	154	908	612	897	765	703

A „nagyot ugró” elemek: 275, 503, 426, 512, 509, 908, 677, 897. Összevethetjük az eredeti (1. sor) és a majdani végleges (3. sor) helyzetüket a pillanatnyival (5. sor). A 2. és a 4. sorban a végleges helyétől vett távolság látható.

503	87	512	61	908	170	897	275	653	426	154	509	612	677	765	703
6	0	6	3	11	2	8	3	2	4	8	4	3	2	1	3
61	87	154	170	275	426	503	509	512	612	653	677	703	765	897	908
4	0	3	3	3	2	4	1	2	1	8	4	3	1	1	3
275	87	426	61	509	170	677	503	653	512	154	908	612	897	765	703

A távolságösszeg jócskán csökkent: 66®43. (Mindezt 15 összehasonlítással értük el. Összevetve az előbbi példával: ott 15 összehasonlítás után jóval 50 fölött találnánk a távolságösszeget.)

Ha most már 5-ös rendezést végzünk:

275	87	426	61	509	170	677	503	653	512	154	908	612	897	765	703
154	87	426	61	509	170	677	503	653	512	275	908	612	897	765	703

Folytassuk 3-asával:

154	87	426	61	509	170	677	503	653	512	275	908	612	897	765	703
61	87	170	154	275	426	512	503	653	612	509	765	677	897	908	703

Majd 1-esével:

61	87	170	154	275	426	512	503	653	612	509	765	677	897	908	703
61	87	154	170	275	426	503	509	512	612	653	677	703	765	897	908

Fontosnak látszó kérdés: hogyan változzék a lépésköz.

Szempontok, megfontolások:

· Ne „aprónként” változzék, mert akkor nagyon sok lépést kell tenni, sőt valószínűleg nagyot már nem is tudna mozdítani az elemeken egy kb. ugyanakkora lépésközű „újrarendezés”. Pl. feleződjön!

· Relatív prímek legyenek az egymást követő lépésközök, mert ellenkező esetben sok elemet ugyanabba a részsorozatba sorolván, fölöslegesen hasonlítjuk egymáshoz. Pl. csökkenő prímek!

Ezek után maga az algoritmus, amely alapja a már ismert javított beillesztéses rendezés.

Alg:

Eljárás ShellRendezés(Konstans N:Egész, Változó X:THk):
Változó
i,j,k,m:Egész
segéd:TH

m:=m0 [kezdő lépésköz]
Ciklus amíg m³1 [lépésköz-ciklus]
Ciklus k=m+1-től 2*m-ig [k: az m. részsorozat 2. eleme]
[Javított beillesztéses rendezés
m-lépésközű sorozatra:]
Ciklus i=k-tól N-ig m-esével
j:=i-m; segéd:=X(i)
Ciklus amíg j>0 és X(j)>segéd
X(j+m):=X(j); j:-m
Ciklus vége
X(j+m):=segéd
Ciklus vége
Ciklus vége
m:=Követező(m)
Ciklus vége
Eljárás vége.

[l0=2^k-1 esetén:]

Függvény Következő(Konstans m:Egész):Egész
[Ef: m=2^k-1]
Következő:=(m+1) Div 2 -1
[uf: Következő(m)=2^k-1-1]
Függvény vége.

vagy [m0,m1=egymást követő Fibonacci-számok esetén
m0,m1 globális változók:]

Függvény Következő(Konstans m:Egész):Egész
[Ef: m,m1=egymást követő Fibonacci-számok]
Változó
mm,m2:Egész
m2:=m-m1; mm:=m1; m1:=m2
Következő:=mm
[Uf: Következő(m),m1=egymást követő Fibonacci-számok]
Függvény vége.
[Pl. m0=m=13, m1=8 Þ (m,m1)=(8,5),(5,3),(3,2),(2,1)]

Megjegyzés:

David Russell (1971) „kimérte” a Shell rendezés hatékonyságát: 100£N£60000 mellett, különböző lépésköz-függvény esetén így találta:

a) m_k=2^k+1 esetén 1.09*N^1.27

b) m_k=2^k-1 esetén 1.22*N^1.26

2. Egy csöpp rendezéselmélet

2.1. Minimális hasonlításszám

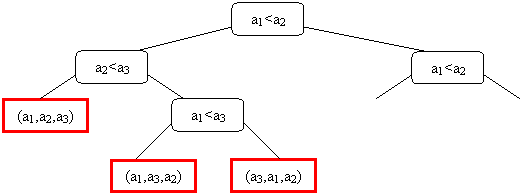
N elem rendezéseinek feleltessünk meg az ún. döntés (összehasonlítási) v. végrehajtási fát!

Pl. (a₁,a₂,a₃) Þ

A fa leveleinek száma 3 elem permutációinak száma: 3!=6. N elem esetén N! .

Állítás:

A rendezés hasonlításainak száma elemszám függvényében H(n) Î W(n*log(n))

Bizonyítás:

1. Rendeljük az n elemű sorozathoz a döntési fát!

2. Ekkor a permutációk száma: n!, ami éppen a leveleinek száma.

3. Legyen h:=a magassága, azaz leghosszabb ágának hossza (vagyis a legkedvezőtlenebb esetben a szükséges hasonlítások száma).

4. Ekkor egy bináris fának legfeljebb (a teljes bináris fának pontosan) 2^h levele van.

Azaz n!£ 2^h. Innen h³log(n!).

A Stirling-formula legegyszerűbb alakját (n!»(n/e)ⁿ) felhasználva:

H(n) ³ log(n!) » n*log(n)-n*log(e) Þ HÎW(n*log(n))

(A HÎW(n*log(n)) belátása:

keressük olyan cÎR₊-t és n₀ÎN, amelyre "n³n₀-re teljesül

n*log(n)-n*log(e)³c*n*log(n)

c-re rendezve:

1 – log(e)/log(n)³c

Legyen pl. c:=0,5, akkor n₀ határindexnek megfelelő lesz:

1 – log(e)/log(n)³0,5 Û 0,5³log(e)/log(n) Û log(n)³2*log(e) Û n³e²=n₀.)

Q.e.d.

2.2. Minimális mozgatásszám

N elem rendezése úgy, hogy a lehető legkevesebb mozgatást végezze az algoritmus.

Megoldás nyilván a szétosztó rendezés. Hátránya, hogy

1. Megduplázza a helyigényt (sőt).

2. Komoly előzetes elvárással él (Kulcs=rendezés szerint hely indexe).

Tegyük föl (anélkül, hogy magát az algoritmust keresnénk), hogy valahonnan rendelkezésre áll a rendezési index-információ[7], s ezután kell a minimális mozgatást megvalósítanunk. Tehát a sorozat megduplázása nélkül, helyben helyretételre kell módszert találnunk.

Lássunk egy számpéldát! Jelölje S a sorozat elemeit, az elem indexét az I, és a rendezettség szerinti helyének indexét RI (RendIndex).

I:	1	2	3	4	5	6	7
RI:	2	7	1	5	3	6	4
S:	20	70	10	50	30	60	40

A helyrerakás lépései:

1. Helyet csinálunk – az S(1)-ben.

I:	1	2	3	4	5	6	7
RI:		7	1	5	3	6	4
S:		70	10	50	30	60	40
	2
	20

Ekkor már helyére tehetjük az 1. helyre valót: a 10-et.

I:	1	2	3	4	5	6	7
RI:	1	7		5	3	6	4
S:	10	70		50	30	60	40
	2
	20

A felszabadult 10 helyére való a 30.

I:	1	2	3	4	5	6	7
RI:	1	7	3	5		6	4
S:	10	70	30	50		60	40
	2
	20

és így tovább…

I:	1	2	3	4	5	6	7
RI:	1	7	3		5	6	4
S:	10	70	30		50	60	40
	2
	20

I:	1	2	3	4	5	6	7
RI:	1	7	3	4	5	6
S:	10	70	30	40	50	60
	2
	20

I:	1	2	3	4	5	6	7
RI:	1		3	4	5	6	7
S:	10		30	40	50	60	70
	2
	20

Már csak az előzetesen kimentett 20-at kell visszatennünk, és kész.

I:	1	2	3	4	5	6	7
RI:	1	2	3	4	5	6	7
S:	10	20	30	40	50	60	70

(Ne is vegyük észre, hogy a 60 meg sem moccant!)

De nézzük az alábbi, picit módosított példát:

I:	1	2	3	4	5	6	7
RI:		3	1	5	7	6	4
S:		30	10	50	70	60	40
	2
	20

Ugyanúgy járunk el, ahogy előbb:

I:	1	2	3	4	5	6	7
RI:	1	3		5	7	6	4
S:	10	30		50	70	60	40
	2
	20

I:	1	2	3	4	5	6	7
RI:	1		3	5	7	6	4
S:	10		30	50	70	60	40
	2
	20

… és máris visszatehető a 20, sőt egyebet sem tehetünk.

I:	1	2	3	4	5	6	7
RI:	1	2	3	5	7	6	4
S:	10	20	30	50	70	60	40

De baj van: nem vagyunk még készen! :-(

…

A probléma: a permutáció gyakorta (sőt többnyire) –csoportelméleti szóhasználat szerinti– ún. ciklusok szorzata, amelyeken belül az elemek egymástól függetlenül permutálhatók a helyükre. A fenti példa ciklusok szorzatára bontva: (132)(754)(6).

Alg:

Konstans MaxN:Egész(???)
Típus THk= Tömb(1..MaxN:TH)
TIndk=Tömb(1..MaxN:0..MaxN) [=0ÞOK; =0Þi. helyre való]
TKeresett=Rekord(van:Logikai, hol:Egész)

Eljárás Helyretétel(Konstans N:Egész, Változó[8] Ind:TIndk
[Változó] S:THk):
Változó
j:Egész
tovább:TKeresett

tovább.hol:=1; tovább.van:=Igaz
Ciklus amíg tovább.van
EgyCiklusHelyre(tovább.hol,Ind,S)
tovább:=Keresés(Ind,¹0) [van még ciklus? hol?]
Ciklus vége
Eljárás vége.

Eljárás EgyCiklusHelyre(Változó j:Egész,
Ind:TIndk, S:THk):
Változó
r:TH
i:Egész

r:=S(j) [S(j) fölszabadítása]
Ind(j):=0 [ez már rendben lesz]
Ciklus amíg Ind(j)¹0
i:=Kiválasztás(Ind,=j) [hol van a j-vel egyező indexű?]
S(j):=S(i) [S(i) helyretétele, fölszabadítása]
Ind(i):=0 [ez már rendben lesz]
j:=i
Ciklus vége
S(j):=r
Eljárás vége.

Hatékonysági elemzés:

:=TH	=TH,£TH	:=N	=N,£N	Indexelés	TH	N
EgyCiklusHelyre
2+cj*1	0	(O(N)*cj+	O(N)*cj	O(N)*cj	1	1
		Kiválasztás*cj
		+3*cj)+1		+4
2+cj	0	(O(N)+3)*cj+1	O(N)*cj+1	O(N)*cj+4	1	1
HelyreTétel (Sj cj = c)
Sj 2+cj	0	O(N)*c	O(N)*c	O(N)*c	0	3
		Keresés*c
		+1)		+4
O(N)	0	Sj O(N) +1	Sj O(N)	Sj O(N)	0	3
O(N)	0	O(N)	O(N)	O(N)	1	4

Tartalom

ProgramozásMódszertan 5. előadás’2004 (vázlat) 1

1. Rendezési tételek. 1

1.1. Rendezési tételekről előzetesen. 1

1.1.1. A feladat 1

1.1.2. Fajtái 1

1.1.3. Algoritmikus „filozófiák”. 2

1.1.4. A hatékonyságról 2

1.1.5. A specifikációjukról 3

1.2. Belső rendezések. 4

1.2.1. Egyszerű cserés rendezés. 4

1.2.2. Minimumkiválasztásos rendezés. 4

1.2.3. Buborékos rendezés. 5

1.2.4. Javított buborékos rendezés. 6

1.2.5. Beillesztéses rendezés. 6

1.2.6. Javított beillesztéses rendezés. 7

1.3. Speciális rendezések. 7

1.3.1. Szétosztó rendezés. 7

1.3.2. Számlálva szétosztó rendezés. 8

1.3.3. Számláló rendezés. 9

1.4. Shell rendezés. 10

2. Egy csöpp rendezéselmélet 13

2.1. Minimális hasonlításszám.. 13

2.2. Minimális mozgatásszám.. 13

---

[1] Persze N helyett megfelelő bármely „közismert” rendezett halmaz. Pl.: R, Z, S (=Szövegek halmaza) stb.

[2] Ajánlható ehhez az alábbi irodalom:

· Cormen et al.: Algoritmusok, Műszaki Könyvkiadó, 1997 [18-34. oldalak]

· Knuth: A számítógép-programozás művészete 3., Műszaki Könyvkiadó, 1988

[3] Azért éppen N®N függvény, mert a feladat szempontjából érdekes sorozat hossza függvényében szeretnénk meghatározni bizonyos gyakoriságszerű programjellemzők tendenciáját (ezért aszimptotikusan).

[4] Ki- és bemenő paraméter egyben, ezért változó.

[5] A csere-eljárás később is elő fog bukkanni, de akkor már nem deklaráljuk újra.

[6] A”+1” az s TH-típusú segédváltozó.

§ Az X(i).Kulcs-csal indexelést az inkrementálásban és a dekrementálásban csak egyszer számolva.

[7] Láttuk a számláló rendezésnél, ilyen információ megszerezhető.

[8] Bár nem kimeneti szerepű az adat!