Ebben a leckében két nagy anyagrész található. Az egyik célja, hogy a középiskolai kémia tananyag egy problémakörének, a reakciókinetikának, amely egyszerű matematikai eszközökkel nehezen leírható, szimulációs megoldását adja. A másik az ún. mintázatképződés lényegét és modellezésének mikéntjét mutatja be.
A reakciókinetika a gimnáziumok első osztályának kémia tantervében szerepel először az iskolai tanulmányok során. Ezzel a témakörrel 3-4 órát lehet foglalkozni a gyerekek érdeklődésétől függően, de fakultatív órákon vagy tagozaton mód van részletesebb tárgyalására is.
A reakciókinetika bevezetésénél két szempontot tartunk fontosnak.
1. A kísérletezés semmivel sem pótolható. A tanulók számára mindenféle meggondolás, matematikai levezetés és kémiai leírás a valóságról akkor meggyőző száz százalékosan, ha közvetlen tapasztalhatják, láthatják.
2. Törekedni kell a kémiai fogalmak minél pontosabb, egzaktabb meghatározására és lehetőleg matematikai eszközökkel való leírására.
A reakciókinetika fő feladata a kémiai folyamatok sebességének tanulmányozása és mechanizmusának felderítése. A természetben megfigyelhető folyamatok ritkán játszódnak le tisztán és egyedül. Rendszerint több folyamat egymással (több kémiai, ill. kémiai, fizikai és biológiai együttesen) bonyolult kombinációban zajlik le. Éppen ezért, a természet jelenségeinek részekre bontása, analízise után juthatunk csak el a tanításban közvetlenül felhasználható, az ismeretek kiindulási alapjául szolgáló modellhez, illetve kémiai kísérlethez. A reakciómechanizmus pontos leírásához ismertetni kell az atomok kötésviszonyait, egymáshoz való térbeli elhelyezkedését, a rendszer energiaállapotának változását a reakció folyamán. Lehetetlen ilyen részletesen leírni a molekulák mozgását a reakció folyamán, hiszen igen nagyszámú molekula viselkedésének összegeként kapjuk a reagáló rendszer összes közbenső állapotait. A tapasztalat szerint nemcsak különböző reakciók lefolyása igényel igen különböző időket, hanem ugyanazon reakció sebessége is tág határok között változtatható. A reakciók időbeli lefolyásának tanulmányozása arra a felismerésre vezetett, hogy a legtöbb reakció összetett, vagyis több egymás után vagy egymás mellett végbemenő egyszerű reakcióból áll. Az összetett reakciókat felépítő egyszerű reakciókat reakciólépéseknek vagy elemi reakcióknak nevezzük.
Az elemi reakciókra a következő jegyek jellemzők:
Egy kémiai folyamat reakciómechanizmusát akkor ismerjük, ha megállapítottuk, hogy milyen elemi reakciókból tevődik össze, és kiderítettük az elemi lépéseket meghatározó tényezőket.
Az összetett reakciók mindegyikére általánosan jellemző, hogy
A reakciókinetikában a folyamatokat többféle szempont szerint szokás osztályozni:
Mind a homogén, mind a heterogén kémiai reakciók ugyanakkor lehetnek pl. termikus, fotokémiai, radiokémiai, sugárkémiai reakciók aszerint, hogy a kémiai átalakításhoz szükséges gerjesztő energiát a hő-, a fény-, a sugárzási energia vagy az elektromos energia szolgáltatja.
Tekintsünk egy állandó térfogatú és hőmérsékletű rendszert (lombikot, reaktort stb.), állandó nyomáson, amelyben különböző kémiai komponensek (molekulák, gyökök, ionok) vannak jelen. Ezek között a komponensek között elemi reakciók zajlanak le, amelyeknek hatására a komponensek mennyisége (koncentrációja, darabszáma) az idő múltával megváltozik. A komponensek mennyiségének időbeli változása áll vizsgálódásunk középpontjában. Hosszabb idő átlagában a komponensek mennyiségének térbeli eloszlását homogénnek tekintjük.
Szimulációs modellünkben a reakciótérnek egy N×M-es táblázatot fogunk megfeleltetni. A reakcióteret folytonosan figyeljük, amelyben egy lépésben egy esemény következhet be, tehát a folytonos keretmodell módszerét használjuk. A modell idejének nincs szoros kapcsolata a valós idővel.
Megadhatjuk a molekulák mennyiségét, az átalakulás szabályait, így megfigyelhetővé válik a reakció során a komponensek aránya. Érdekes paramétereket kísérletezhetünk ki adott reakciókhoz.
A modell működése a következő: Az N×M-es táblázatban a molekulákat jelölő betűket véletlenszerűen (nagyjából egyenletesen) helyezzük el. Homogén reakciók esetében minden komponens azonos fázisban van.
Véletlenszerűen kiválasztjuk a reakciótér valamely elemét, majd az ott levő molekulát valamely véletlenszerű szomszédjával megcseréljük vagy módosítjuk a táblázatot a kémiai reakciólépés alapján. A változást a képernyőn jelezzük.
A táblázatból valamely kiválasztott elem cseréje véletlenszerűen meghatározott szomszédjával a hőmozgást jelenti. Egy elem szomszédságába azok a más elemek tartoznak, amelyeket egy molekula időegység alatt elérhet. A legegyszerűbb modellben a szomszédságot egységnyinek tekintjük. Ez nagyon erős megkötés, főleg ha figyelembe vesszük, hogy eleve csak kétdimenziós a rendszerünk. Különböző hőmérsékleteket, csak különböző nagyságú szomszédsággal lehetne figyelembe venni.
Szimulációs lépés:
(i,j):=véletlen hely(N,M)
(k,l):=véletlen szomszéd(i,j)
Reakciólépés T(i,j) és T(k,l) alapján
Csere(T(i,j),T(k,l))
Eljárás vége.
E folyamat során az egymásra ható anyagokból egyetlen új anyag keletkezik. Az ütközés során új kémiai kötés alakul ki. A folyamat általános reakcióegyenlete:
Az egyesülési reakció lefutása a kiindulási anyagok közötti reakciókészség nagyságától és külső körülményektől függően igen különböző lehet. Nézzünk néhány egyszerű példát az egyesülésre.
Égési folyamat a
Ilyen pl. az ózon képződése is elektromos kisülések hatására, amikor a kisüléskor keletkező atomos oxigén a molekuláris oxigénnel ózonná egyesül.
Összefoglalva: a reakció sebessége függ a hőmérséklettől, a nyomástól és a kezdeti koncentrációktól. Az egyesülés beindulásához szükséges energiát melegítés, fény illetve elektromos kisülés biztosíthatja. Az egyesülés sebessége a két kiindulási anyag koncentrációjának szorzatával arányos.
k az egyesülés reakciósebességi állandója. [A] és [B] az A és B molekulák pillanatnyi koncentrációja, amelyeket adott reakciótér esetén a molekulák számával helyettesítek. A és B molekula találkozásánál, a reakciósebességi állandóval arányos, átalakulási valószínűséggel (ÁT) a molekulák C molekulává egyesülnek. A koncentrációk időfüggését analitikusan megoldva ábrázoljuk a függvényeket:
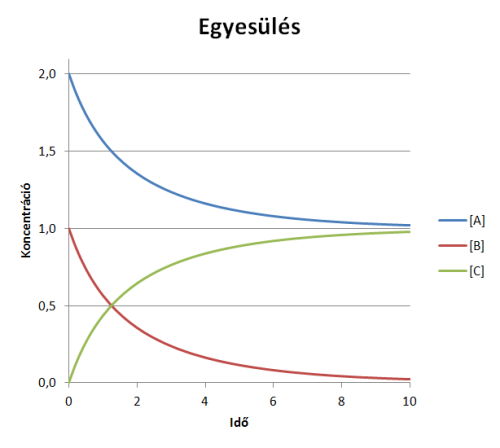Az egyesülés reakcióAz azonos típusú molekulákat nem különböztetjük meg, azaz a molekulák alakjától és az energia eloszlásától nem függ az átalakulás valószínűsége. A kinetikusan másodrendű reakciók gázfázisban és oldatban egyaránt gyakoriak. Modellünkkel zárt, homogén reakciót vizsgálunk.
Egyesülés:
(i,j):=véletlen hely(N,M)
(k,l):=véletlen szomszéd(i,j)
Ha (T(i,j)="A" és T(k,l)="B") vagy (T(i,j)="B" és T(k,l)="A")
akkor Ha véletlenszám<ÁT akkor T(i,j):="C"; T(k,l):=""
Csere(T(i,j),T(k,l))
Eljárás vége.
A programmal megfigyelhető, hogy időben hogyan változik a kiindulási és végtermék anyagok mennyisége, ha a kezdeti feltételeket beállítottuk. Kezdetben a reakciósebesség nagy, ami fokozatosan csökken. A vagy B anyag elfogyása után az átalakulás leáll, a "hőmozgás" folytatódik.
Példa az ÁT=0,5 értékére:
Az egyesülés reakció szimulációjaA reakciósebességi állandót változtatva befolyásolni tudjuk az átalakulás sebességét.
Ha a kiindulási anyagok részecskéinek száma nagyon eltér, akkor a reakció gyorsan lejátszódik. Ebben az esetben a jellemzők a nagyobb mennyiségben jelenlevő anyag részecskéinek számától függ. A program homogén rendszerben lezajló egyesülést szimulál, tehát a részecskék kezdetben is egyenletesen oszlanak el a reakciótérben. Heterogén rendszerben lezajló folyamat mechanizmusa és jellemzői jelentősen eltérnének.
Ez a reakció az egyesüléssel ellentétes folyamat.
Általános egyenlete:
A bomlásnál általában nagyobb összetett vegyületek lebontása megy végbe. Legtöbb esetben hevítés hatására következik be ez a kinetikusan elsőrendű reakció. Például:
A bomlás reakciósebessége:
A reakció sebessége egyetlen anyag koncentrációjával arányos. C anyag mennyisége az idővel exponenciálisan csökken. A csökkenés mértéke a reakciósebességi állandóval megváltoztatható.
differenciálegyenletet integrálni kell. A kezdeti koncentráció legyen [C0].
Már ennél a kinetikai szempontból legegyszerűbb esetben is differenciálegyenletet kellett felállítani, majd azt megoldani. A folytonos keretmodellünkkel más utat járunk.
A bomlás monomolekuláris, tehát nincs szükség molekulák ütközésére a reakció lejátszódásához. Az átalakulási valószínűség (ÁT) azt mutatja meg, hogy időegység alatt egy molekula milyen eséllyel bomlik el. Szimulációs programunkban a bomlás feltétele az is, hogy a bomló molekula környezetében mindig kell lenni szabad helynek. Ez a feltétel azt jelenti, hogy kezdőállapotként csak kis mennyiségeket érdemes megadni az anyagokból.
Bomlás:
(i,j):=véletlen hely(N,M)
Ha T(i,j)="C" és Van Szomszéd(i,j,k,l)
akkor Ha véletlenszám<ÁT akkor T(i,j):="A"; T(k,l):="B"
különben (k,l):=véletlen szomszéd(i,j)
Elágazás vége
Csere(T(i,j),T(k,l))
Eljárás vége.
Programunkkal megfigyelhető, hogy C anyagmennyisége az idővel exponenciálisan csökken, tehát a modell jól visszaadja a differenciálegyenlet megoldását. A reakciósebesség befolyásolható az átalakulási valószínűség megváltoztatásával. C molekula bomlásával az A és a B molekulákból azonos mennyiségű keletkezik.
Példa az ÁT=0,1 értékére:
Az bomlási reakció szimulációjaAz összetett reakciók között aránylag a legegyszerűbbek az egyensúlyra vezető folyamatok, vagyis az olyan egyszerű reakciók, amelyekben előbb-utóbb észrevehetővé válik az ellentétes folyamat, így egy idő múlva beáll az egyensúlyi állapot.
A képződés bimolekulás, a bomlás monomolekulás. A reakciósebességek:
Az egész folyamat bruttó sebessége
Megfelelő idő elteltével v=0-vá válik, ekkor a makroszkopikus bruttó folyamat megáll, egyensúly áll be. Az összes résztvevő anyagok számottevő koncentrációban vannak jelen. Az egyensúly dinamikus jellegű. Az egyensúly elérésének ideje függ a kiindulási koncentrációktól és a reakciósebességi állandóktól (ÁT, VISSZA).
Ilyen folyamat például:
Az egész folyamat bruttó sebessége:
v2 kezdetben nulla, s nő az időben, v1 pedig csökken, s megfelelő idő elteltével egyenlővé válnak.
Elvileg minden reakció megfordítható, de sok folyamat egyensúlya a termékek oldalára tolódik el. Ilyen esetekben a folyamat gyakorlatilag egy irányú, s lezajlása után a kiindulási anyagok mennyisége észrevehetetlen kicsi. Ennek feltétele, hogy k1 nagyságrendekkel nagyobb, mint k2.
Disszociáció:
(i,j):=véletlen hely(N,M)
(k,l):=véletlen szomszéd(i,j)
v:=véletlenszám
Elágazás
T(i,j)="A" és T(k,l)="B" vagy T(i,j)="B" és T(k,l)="A"
esetén Ha v<ÁT akkor T(i,j):="C"; T(k,l):=""
T(i,j)="C" és Van Szomszéd(i,j,k,l)
esetén Ha v<VISSZA akkor T(i,j):="A"; T(k,l):="B"
Elágazás vége
Csere(T(i,j),T(k,l))
Eljárás vége.
Programunkkal megfigyelhető, hogy az egyensúly elérésének ideje függ a kezdőfeltételként megadott anyagmennyiségektől, azaz a kezdő állapot mennyire tér el az egyensúlyi állapottól, és a sebességi állandóktól.
Nagyobb reakciósebességi állandók esetén az egyensúly gyorsabban beáll. Az egyensúly dinamikus jellege jól megfigyelhető, mert a molekulák száma ebben az állapotban is ingadozik.
Példa az ÁT=0,2 és VISSZA=0,3 értékére:
A disszociációs reakció szimulációjaA disszociációs folyamatok speciális esetének tekinthetjük az izomerizációs reakciókat.
A képződés és a visszaalakulás is monomolekulás. Ilyen folyamat például az ammónium-cianát (NH4OCN) átalakulása karbamiddá (CO(NH2)2):
Az átalakulás és a visszaalakulás valószínűsége általában nem egyezik meg, a reakciósebességi állandók értéke hőmérsékletfüggő.
A szerves kémia legtöbb átalakulása több egymás után következő reakciótípusban megy végbe, e lépések alkotják a sorozatreakciók rendszerét. Egy ilyen rendszer legegyszerűbb esete két egymás után következő elsőrendű reakció.
E két lépésből álló rendszernek a megfelelő reakciósebbességi állandói k1, k2. A kiindulási anyag, a köztitermék és a végtermék koncentrációjának időbeli változását a következő függvények írják le.
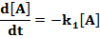
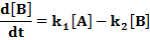
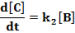
Ezeket az egyenleteket megoldva a megfelelő koncentrációk az idő függvényében:
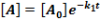
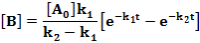
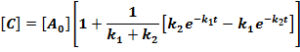
Ezek alapján a koncentrációk az idő függvényében már könnyen ábrázolhatók.
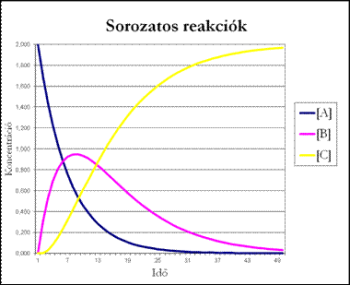
[A] exponenciálisan csökken az időben, [B] eleinte nő, majd maximumon átmenve csökken és hosszú idő múlva nulla felé tart. Ha a folyamat elég lassú, akkor a maximum igen lapos, vagyis a közbenső termék koncentrációja hosszabb időn át állandó marad. A végtermék koncentrációja eleinte lassan nő, mert kezdetben [B] kicsi, majd képződési sebessége megnövekszik, s végül [C] értéke eléri A kezdeti koncentrációjának értékét, ami a teljes átalakulásnak felel meg. Ha k1<<k2 vagy k1 >>k2, akkor a teljes folyamat sebességét a kisebb reakciósebességi állandójú részfolyamat sebessége szabja meg. Ha k1>>k2, akkor a köztitermék és a végtermék koncentrációját kifejező egyenletek tovább egyszerűsödnek:
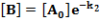
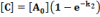
Csak az a közbenső termék halmozódhat fel számottevő mértékben a reakció folyamán, amely a megelőzőhöz képest lassú reakciólépés kiindulási anyaga.
A sorozatos reakciók egyáltalán nem ritkák, nagy szerepet játszanak főként a láncreakciókban és a heterogén kémiai folyamatokban. Több sorozatos lépésben folyik le oldatokban az ionreakciók nagy része is (Például: az SnCl2 oxidációja FeCl3 -dal), és a kétbázisú savak észtereinek elszappanosítása. Legyen ÁT1 az A → B és ÁT2 a B → C reakció átalakulási valószínűsége.
Sorozatos:
(i,j):=véletlen hely(N,M)
(k,l):=véletlen szomszéd(i,j)
Elágazás
T(i,j)="A" esetén Ha véletlenszám<ÁT1 akkor T(i,j):="B"
T(i,j)="B" esetén Ha véletlenszám<ÁT2 akkor T(i,j):="C"
Elágazás vége
Csere(T(i,j),T(k,l))
Eljárás vége.
Az ÁT1=0,3 és ÁT2=0,2 értékű | Az ÁT1=0,3 és ÁT2=0,03 értékű |
|---|---|
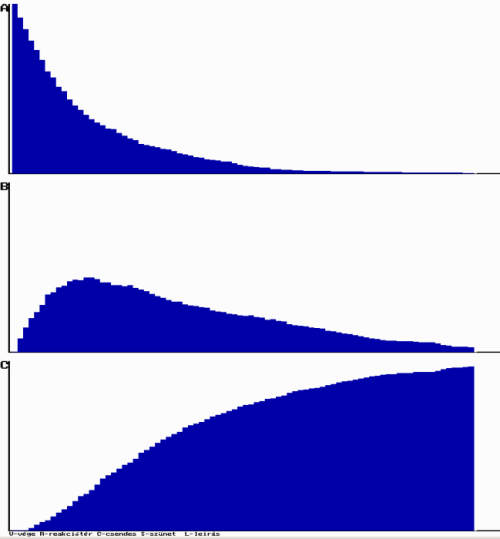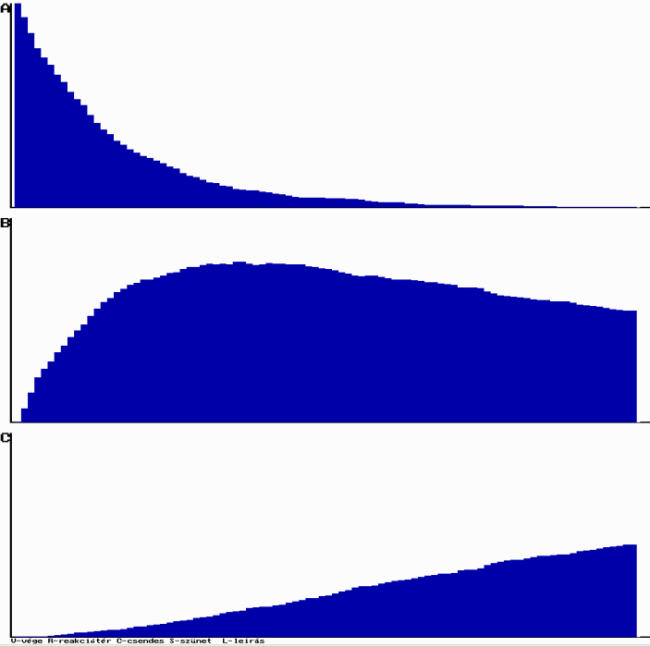 Az sorozatos reakció szimulációja közel azonos reakciósebességi állandó esetén |  Az sorozatos reakció szimulációja lényegesen különböző reakciósebességi állandó esetén |
Programunkkal megfigyelhető, hogy a szimuláció alapján kapott koncentráció-idő függvények lefutása jól megegyezik a differenciálegyenletek megoldásával. Ha k1 és k2 nem tér el jelentősen, akkor B molekula mennyisége a folyamat elején jelentősen megnő, majd fokozatosan csökken, végül nullává válik. Az A molekula mennyisége, mivel monomolekuláris reakcióban bomlik, exponenciálisan csökken. A reakció addig tart, amíg a kiindulási anyag és a köztitermék teljes mennyisége végtermékké nem alakul.
Ugyanazon anyag vagy anyagok különféle kémiai átalakuláson mehetnek át, vagyis adott kiindulási anyagok között sokszor többféle reakció lehetséges.
A párhuzamos reakciók legegyszerűbb példái azok, amelyekben két kinetikusan elsőrendű folyamat megy egymás mellett végbe. Ilyen például a fenol nitrálása, amikor elsőrendű folyamatban orto- és para-nitrofenol keletkezik.
-szintézisgázból metanol illetve metán keletkezése
-a kálium-klorát mérsékelten hevítve kétféleképpen bomlik:
A két reakció sebessége igen különböző lehet. Mindkét termék keletkezésének időbeli lefolyását a bruttó sebességi állandó, a termékek arányát viszont a párhuzamos folyamatok sebességi állandóinak viszonya szabja meg. Az egyes párhuzamos részfolyamatok sebességi állandója különböző mértékben változik a hőmérséklettel, a katalizátorok is különböző hatással vannak a részfolyamatokra. A körülmények megfelelő megválasztásával gyakran megvalósítható, hogy az egyik folyamat sebessége túlnyomóvá váljék az összes többi mellett. Ha a párhuzamos folyamatok egyikének sebessége lényegesen nagyobb a többinél, akkor azt főreakciónak, a többit mellékreakcióknak nevezzük. Gyakorlatilag azért fontos, mert ez lehetővé teszi különböző termékek előállítását ugyanazon kiindulási anyagból, vagyis a folyamat irányítását.
Ha a két párhuzamos folyamat sebességi állandói k1 és k2, az A anyag koncentrációja időben exponenciálisan csökken. Legyen k=k1 +k2.
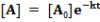
A termékek mennyiségének növekedését leíró differenciálegyenletek:
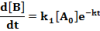
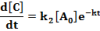
Az egyenleteket nullától t-ig integrálva megkapjuk a két termék koncentrációját t időpontban:
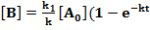
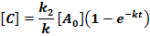
Mindkét termék keletkezésének időbeli lefolyását a bruttó sebességi állandó (k), a termékek arányát viszont a párhuzamos folyamatok sebességi állandóinak viszonya szabja meg:
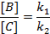
Legyenek a két párhuzamos lépés sebességi állandói ÁT1 és ÁT2!
Párhuzamos:
(i,j):=véletlen hely(N,M)
(k,l):=véletlen szomszéd(i,j)
v:=véletlenszám
Ha T(i,j)="A" akkor Ha v<ÁT1 akkor T(i,j):="B"
különben Ha v<ÁT1+ÁT2 akkor T(i,j):="C"
Elágazás vége
Csere(T(i,j),T(k,l))
Eljárás vége.
Példa az ÁT1=0,2 és ÁT2=0,05 értékére:
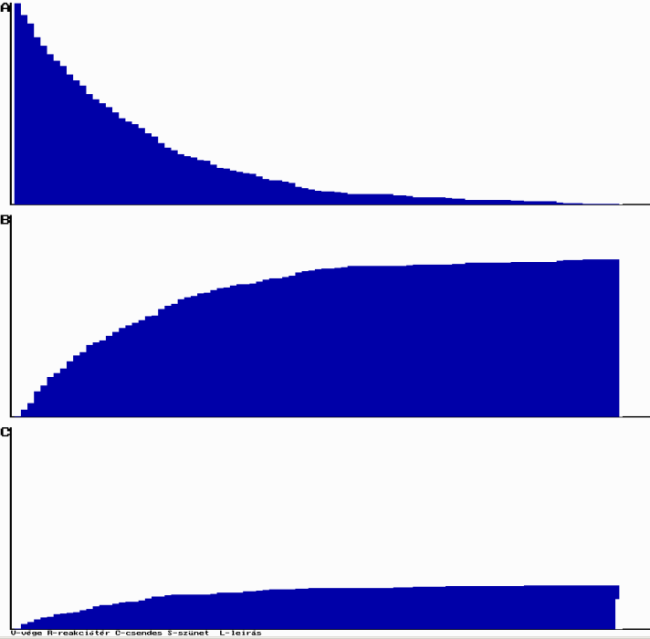A párhuzamos reakciók szimulációjaProgramunk által szimulált folyamatban a koncentrációviszonyok azonos módon változnak, mint ahogy a differenciálegyenletek alapján várható volt.
Modellünkkel megfigyelhetjük, hogy a párhuzamos folyamatok bruttó sebességét főleg a leggyorsabb részfolyamat szabja meg. Ha k1 jóval nagyobb, akkor szinte csak B molekulák keletkeznek. Az A molekulák teljes átalakulása után a reakció leáll.
Olyan sorozatreakció, amely reverzibilis lépést tartalmaz.
Ilyen reakció a dinitrogén-pentoxid bomlása homogén gázfázisban.
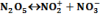
A keletkezett nitrát szabad gyök, amely ugyan a legnagyobb valószínűséggel újra egyesül a nitrozil kationnal, sokkal kisebb valószínűséggel azonban elbomlik:
A második lépés a sebesség meghatározó, mivel ez a leglassúbb. A kiindulási anyag, a köztitermék és a végtermék koncentrációjának időbeli változását egzakt matematikai eszközökkel nem tudjuk megadni. A reakciósebességi állandók aránya nagy mértékben befolyásolja ezeket. Programunkban legyen: az A →B reakciósebességi állandója ÁT1, a B → A-é ÁT2 és a B → C-é ÁT3!
KombináltI:
(i,j):=véletlen hely(N,M)
(k,l):=véletlen szomszéd(i,j)
v:=véletlenszám
Elágazás
T(i,j)="A" esetén Ha v<ÁT1 akkor T(i,j):="B"
T(i,j)="B" esetén Ha v<ÁT2 akkor T(i,j):="A"
különben Ha v<ÁT2+ÁT3 akkor T(i,j):="C"
Elágazás vége
Csere(T(i,j),T(k,l))
Eljárás vége.
Programunkkal megfigyelhető, ha ÁT1 és ÁT3 jóval nagyobb, mint ÁT2, akkor B köztitermék nagyon alacsony mennyiségben van jelen.
Ha ÁT1 jóval nagyobb, mint a másik kettő reakciósebességi állandó, akkor B mennyisége rövid idő után megnő és állandó marad (kvázistacionárius állapot) B molekula teljes mennyiségének C-vé bomlásáig.
Ha ÁT3 jóval kisebb, mint a másik kettő reakciósebességi állandó, akkor A és B molekulák közötti egyensúly lassan szűnik meg B-nek C-vé alakulásával.
Példa az ÁT1=0,3; ÁT2=0,6 és ÁT3=0,15 értékére:
A kombinált I. reakciók szimulációjaIlyen jellegű reakciók a heterogén folyamatoknál gyakoribbak, mivel valamely reagens a reakció fázisából való távozása (csapadékképződés vagy folyadék fázisú reakciók gázképződéssel) nem megfordítható folyamatoknak tekinthetők. Ezek a rendszerek már nem tekinthetők zártnak.
Több sorozatos lépésben folyik le oldatokban az ionreakciók nagy része is.
Például az SnCl2 oxidációja FeCl3 által:
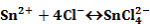
Ebben az előegyensúlyban képződött komplex ionok két lépésben adják át elektronjaikat a Fe3+-ionoknak:
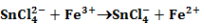
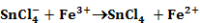
Olyan párhuzamos reakció, amely reverzibilis lépést is tartalmaz.
Az A, B és C molekulák koncentrációjának időbeli változását a reakciósebességi állandók aránya határozza meg. A reakció befejeződése után A és B teljes mennyisége C-vé alakul.
Legyen A → B folyamat reakciósebességi állandója ÁT1, B → A-é ÁT3 és A → C-é ÁT2.
KombináltII:
(i,j):=véletlen hely(N,M)
(k,l):=véletlen szomszéd(i,j)
v:=véletlenszám
Elágazás
T(i,j)="A" esetén Ha v<ÁT1 akkor T(i,j):="B"
különben Ha v<ÁT1+ÁT2 akkor T(i,j):="C"
T(i,j)="B" esetén Ha v<ÁT3 akkor T(i,j):="A"
Elágazás vége
Csere(T(i,j),T(k,l))
Eljárás vége.
A szimuláció hasonlóan a Kombinált I. reakcióhoz az A és B molekulák C-vé alakulásával fejeződik be. Ha ÁT2 kicsi akkor az A és B molekulák közötti egyensúly sokáig megmarad, illetve mennyiségük párhuzamosan és lassan csökken.
Ha ÁT1 jóval nagyobb a többihez képest, akkor először az A teljes mennyisége B-vé alakul át és az, természetesen A-n keresztül, lassan alakul csak C-vé.
Példa az ÁT1=0,4; ÁT2=0,3 és ÁT3=0,05 értékére:
A kombinált II. reakciók szimulációja 1.Ha ÁT1 kicsi a többi sebességi állandóhoz képest, akkor a B molekula mennyisége szinte elhanyagolható.
Példa az ÁT1=0,1; ÁT2=0,3 és ÁT3=0,2 értékére:
A kombinált II. reakciók szimulációja 2.A katalizátorok olyan anyagok, amelyek jelenlétükkel meggyorsítják a kémiai reakciókat, illetve megváltoztatják azok irányát anélkül, hogy a reakció folyamán maradandóan átalakulnának, és az egyensúlyt megváltoztatnák.
(A katalizátorok nemcsak gyorsíthatják, hanem lassíthatják is egy reakció lefolyását. Az első esetben katalizátorokról, az utóbbiban inhibitorokról beszélünk.) Ha a katalitikus folyamat egynemű fázisban játszódik le, homogén katalízisről, ha viszont a reakció két fázis határán megy végbe, heterogén katalízisről beszélünk. Ha a katalizátor a reakció folyamán keletkezik, akkor autokatalízisről beszélünk.
A katalizáló hatás általában abban áll, hogy a katalizátor az egymásra ható anyagok valamelyikével aktív átmeneti komplexummá egyesül, s ez alakul át a végtermékké. Az átmeneti komplexum aktív volta abban mutatkozik, hogy képződésének és bomlásának a sebessége egyaránt nagyobb, mint a kiindulási anyagok közvetlen reakciójának sebessége.
A katalizátorok a reakciók aktiválási energiáját csökkentik. Ennek megfelelően adott hőmérsékleten nagyobb számú molekulának van a reakció megindításához szükséges energiája, tehát több ütközés lesz hatásos, a reakció meggyorsul. Mivel a katalizátor a reakció végén eredeti állapotába kerül, kis mennyiségű katalizátor igen nagy mennyiségű anyag átalakulását gyorsíthatja meg. A homogén katalitikus reakciók olyan párhuzamos reakcióként foghatók fel, ahol a katalitikus folyamat sebességi állandója sokkal nagyobb, mint a termodinamikailag ugyancsak lehetséges nemkatalizált direkt lépés sebességi állandója.
A katalízisek mechanizmusa igen különböző, Pl. az acetaldehid termikus bomlásának bruttó reakcióegyenlete:
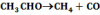
A jódgőz azáltal katalizálja, hogy átmenetileg HI-t képez:
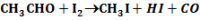
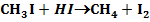
Számos katalizátor láncreakciót indít, s ezáltal gyorsítja a folyamatot. Pl. száraz CO teljesen száraz levegőn lassan oxidálódik. Vízgőz jelenlétében azonban a CO égése gyors. A vízgőz katalitikus hatása, úgy látszik, a következő láncreakciókra vezethető vissza:
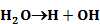
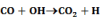
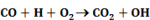
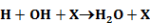
Legyen ÁT1 az A → B és ÁT2 az A + C → B + C folyamat reakciósebességi állandója.
Katalízis:
(i,j):=véletlen hely(N,M)
(k,l):=véletlen szomszéd(i,j)
v:=véletlenszám
Elágazás
T(i,j)="A" esetén Ha v<ÁT1 vagy v<ÁT1+ÁT2 és T(k,l)="C"
akkor T(i,j):="B"
T(i,j)="C" esetén Ha v<ÁT2 és T(k,l)="A" akkor T(i,j):="B"
Elágazás vége
Csere(T(i,j),T(k,l))
Eljárás vége.
Példa az ÁT1=0,02 és ÁT2=0,7 értékére:
A katalízis szimulációjaHa ÁT2 nullával egyenlő, akkor a folyamat katalizátor nélküli monomolekulás átalakulási reakciónak felel meg. Az A molekula mennyisége exponenciálisan csökken, a B molekula mennyisége exponenciálisan nő. Ha C molekulák is jelen vannak (elég kis mennyiségben is), illetve ÁT2 jóval nagyobb ÁT1-nél, akkor a katalitikus folyamat lényege megfigyelhető, az A molekula átalakulási sebessége jelentősen megnő. Ha ÁT2 << ÁT1, akkor C molekula inhibitorként szerepel a folyamatban.
Példa az ÁT1=0,02 és ÁT2=0,0 értékére:
A nem katalizált reakció szimulációjaKatalitikus folyamatok esetében előfordul az is, hogy a katalizátor csak a reakció során termelődik, és mennyisége a reakció előrehaladtával folyton nő.
E rendszer különleges sajátsága az, hogy egyik ciklikus komponense maga a B végtermék. Ezekre a reakciókra az jellemző, hogy katalizátor hiányában először a sebességük igen kicsi (indukciós periódus), majd a B termék megjelenésével rendkívül felgyorsulnak, végül a teljes átalakulás környezetét elérve, az A molekula mennyiségének lecsökkenése miatt, újból lassul a reakció.
Az autokatalitikus rendszer öngyorsuló jellegét röviden úgy indokolhatjuk, hogy benne a katalizátor összes mennyisége a reakció előrehaladtával növekszik.
Például: A kálium-permanganát oxidáló hatását a mangán-ionok katalizálják, amelyek a savanyú közegben való oxidáció közben keletkeznek.
Autokatalízis:
(i,j):=véletlen hely(N,M)
(k,l):=véletlen szomszéd(i,j)
v:=véletlenszám
Elágazás
T(i,j)="A" és T(k,l)="B" vagy T(i,j)="B" és T(k,l)="A"
esetén Ha v<ÁT1 akkor T(i,j):="C"; T(k,l):=""
T(i,j)="C" esetén Ha v<ÁT2 és Van Szomszéd(i,j,k,l)
akkor T(i,j):="B"; T(k,l):="B"
Elágazás vége
Csere(T(i,j),T(k,l))
Eljárás vége.
Programunkkal megfigyelhető, hogy a B molekula mennyisége időben S alakú görbe szerint változik, amely tipikus jellemzője az autokatalitikus folyamatnak. Az indukciós periódus után a reakció exponenciálisan felgyorsul, majd az A mennyiségének igen nagy mértékű lecsökkenése miatt újból lassul, és csak igen lassan éri el a valóban teljes átalakulást.
Példa az ÁT1=0,70 és ÁT2=0,50 értékére:
Az autókatalízis szimulációjaAz egyszerű kémiai reakciókban a termékek koncentrációjának időbeni változása mindig monoton.
Bonyolultabb reakciórendszerek esetén elérhető, hogy pl. az egyik termék koncentrációja az időben ugrásszerűen változzék. A három reakció közül az első a leglassúbb folyamat, és a harmadik a leggyorsabb.
Ilyen jelenséget tapasztalunk akkor, ha a jodidionok és a peroxi-diszulfát-ionok közötti jódképződéssel járó redoxireakciót úgy hajtjuk végre, hogy a reakcióelegyhez kis mennyiségű tioszulfátot adunk, ami gyorsan elfogyasztja a reakció elején képződő jódot. Adjunk az oldathoz híg keményítő oldatot. A koncentrációk pontos beállításával elérhető, hogy az oldatok összeöntése után, megfelelő idő elteltével, az oldat pillanatszerűen kék színű lesz. A végbemenő reakciók egyenlete:
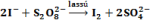
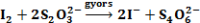
majd a tioszulfát elfogyása után:
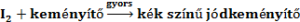
A kék szín megjelenési ideje egy adott, és minden kísérletben állandó tioszulfát-koncentráció esetén fordítva arányos az első lépés reakciósebességével.
A Landolt-reakciót modellezzük az alábbi reakcióegyenletekkel.
Az egyes lépések reakciósebességei rendre ÁT1, ÁT2 és ÁT3.
Landolt:
(i,j):=véletlen hely(N,M)
(k,l):=véletlen szomszéd(i,j)
v:=véletlenszám
Elágazás
T(i,j)="A" esetén Ha v<ÁT1 és T(k,l)="B"
akkor T(i,j):="C"; T(k,l):="D"
különben Ha v<ÁT1+ÁT3 és T(k,l)="E"
akkor T(i,j):="C"; T(k,l):="D"
T(i,j)="B" esetén Ha v<ÁT1 és T(k,l)="A"
akkor T(i,j):="C"; T(k,l):="D"
különben Ha v<ÁT1+ÁT2 és T(k,l)="D"
akkor T(i,j):="E"; T(k,l):=""
T(i,j)="D" esetén Ha v<ÁT2 és T(k,l)="B"
akkor T(i,j):="E"; T(k,l):=""
T(i,j)="E" esetén Ha v<ÁT3 és T(k,l)="A"
akkor T(i,j):="C"; T(k,l):="D"
Elágazás vége
Csere(T(i,j),T(k,l))
Eljárás vége.
Sajnos a szimulációs program nem adja vissza a valóságot.
Példa az ÁT1=0,05; ÁT2=0,2 és ÁT3=0,8 értékére:
A Landolt reakció szimulációjaAz E és a D molekulák számának, az A és a B molekulák számának lecsökkenése után, ugrásszerűen kéne megnőni, ehelyett lassú növekedést tapasztalunk. Az eltérésnek több oka is lehet:
A biológia, illetve a biokémia egyik legfontosabb problémaköre a tápanyag lebontás. Az élő szervezetek már nem tekinthetők zártnak, hiszen a rendszerbe anyag be- és kiáramlás történik. A lebontási folyamat egyik fontos lépése a citromsavciklus, amely részletesen kidolgozott példája a kémiai körfolyamatoknak.
Szimulációs modellünkhöz egyszerűbb rendszert választunk. Nyílt rendszer esetében a legegyszerűbb kémiai körfolyamat:
A kémiai rendszerbe D molekulák belépnek, illetve a reakciótérből az E molekulák kilépnek. Molekulák be- és kilépése diffúzióval történik. Megfigyelhető, hogy a rendszer belső komponenseinek arányai egy idő után stabil értéket vesznek fel, a folyamat stacionáriussá válik. Legyenek az egyes reakciók sebességi állandói rendre: ÁT1, ÁT2 és ÁT3! Legyen a be-, illetve kiáramlás valószínűsége BE, illetve KI! Beáramlás csak akkor történhet, ha a határon szabad helyet találunk, akkor oda a beáramlás valószínűségétől függően D molekula léphet. A reakciótér határáról E molekula meghatározott valószínűséggel kiléphet.
Körfolyamat:
(i,j):=véletlen hely(N,M)
(k,l):=véletlen szomszéd(i,j)
v:=véletlenszám
Elágazás
T(i,j)="" esetén Ha v<BE és (k,l) a Reakciótér határa
akkor T(i,j):="D"
T(i,j)="A" esetén Ha v<ÁT1 és T(k,l)="D"
akkor T(i,j):=""; T(k,l):="B"
T(i,j)="B" esetén Ha v<ÁT2 és Van szomszéd(i,j,k,l)
akkor T(i,j):="C"; T(k,l):="E"
T(i,j)="C" esetén Ha v<ÁT3 akkor T(i,j):="A"
T(i,j)="D" esetén Ha v<ÁT1 és T(k,l)="A"
akkor T(i,j):=""; T(k,l):="B"
T(i,j)="E" esetén Ha v<KI és (k,l) a Reakciótér határa
akkor T(i,j):=""
Elágazás vége
Csere(T(i,j),T(k,l))
Eljárás vége.
A programmal megfigyelhető, hogy a molekulák száma egy rövid kezdeti idő után stabilis értéket vesz fel, a rendszer stacionáriussá válik.
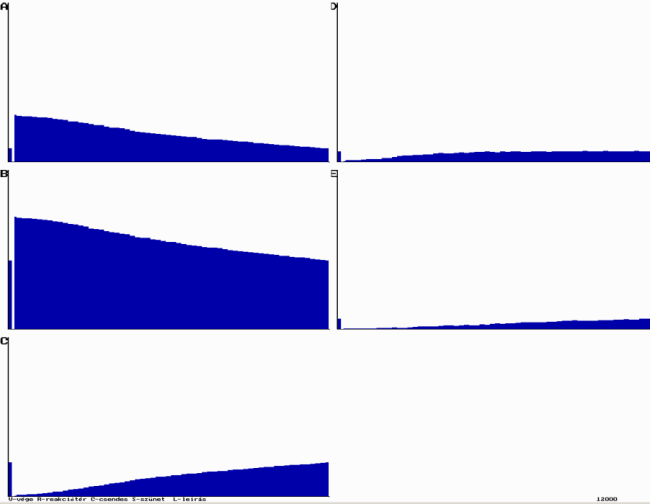
Példa az ÁT1=0,30; ÁT2=0,20 és ÁT3=0,30, valamintBE=0,80 és KI=0,50 értékére:
A körfolyamat szimulációjaA reakciósorozat eredményeként D molekulákból E molekulák keletkeznek. Ez a rendszer jó példája, hogy a reakciómechanizmusok meghatározásához nem elegendő a kiindulási és végtermékek ismerete. (Példánk nem elsőrendű, monomolekulás átalakulási reakció.) A reakciólépések ismerete alapján katalizáltnak is tekinthetjük a reakciót.
Valamennyi, eddig tárgyalt kémiai átalakulás egy tekintetben hasonlít egymásra: a reakcióban résztvevő összes anyag koncentrációja az idő előrehaladtával addig változik, amíg a rendszer egyensúlyba vagy stacionárius állapotba nem kerül. Ezt az állapotot azután megőrzi, a koncentrációk csak külső hatásra változnak újra.
Most megpróbálunk olyan kémiai reakciómechanizmust konstruálni, amely oszcillációra vezet, tehát a benne szereplő egyik vagy másik anyag koncentrációja huzamos ideig (idealizált esetben végtelen hosszan) periodikusan változik. A kísérletek tanúsága szerint léteznek a természetben periodikus reakciók. Pl.: hidrogén-peroxid jodát- katalizálta bomlása. Ebben a rendszerben koncentráció-oszcillációt mutat a köztitermékként megjelenő jodidion és jód, továbbá az oldat pH-ja, valamint oszcillál az oxigénfejlődés sebessége.
Vizsgáljuk a következő több lépésből álló kémiai rendszert:
Bizonyos sebességi állandó értékek esetében B és C koncentrációja időben oszcilláló jelleggel változik, ha [A] és [D] állandó marad (vagyis a rendszer A-ra és D-re nyitott). A mechanizmus azt mutatja, hogy az oszcilláció kialakulásához visszacsatolási reakciókra is szükség van. Az 1. és 2. reakció is autokatalitikus. A bruttó reakció: A → D, a reakció köztitermékei B és C. B és C koncentrációja időben csillapítatlan oszcillációt mutat. A kémiai rendszer távol kell, hogy legyen az egyensúlyi állapottól, amelyet A és D szabad áramlásával biztosítunk.
Oszcillál:
(i,j):=véletlen hely(N,M)
(k,l):=véletlen szomszéd(i,j)
v:=véletlenszám
Elágazás
T(i,j)="" esetén Ha (k,l) a Reakciótér határa
akkor Ha v >0.5 akkor T(i,j):="A"
különben T(i,j):="D"
T(i,j)="A" esetén Ha (k,l) a Reakciótér határa
akkor T(i,j):=""
különben Ha v<ÁT1 és T(k,l)="B" akkor T(i,j):="B"
T(i,j)="B" esetén Ha v<ÁT2 és T(k,l)="B"
akkor T(i,j):="A"
különben Ha v<ÁT3 és T(k,l)="C" akkor T(i,j):="C"
T(i,j)="C" esetén Ha v<ÁT4 és T(k,l)="C"
akkor T(i,j):="B"
különben Ha v<ÁT5 akkor T(i,j):="D"
T(i,j)="D" esetén Ha (k,l) a Reakciótér határa
akkor T(i,j):=""
különben Ha v<ÁT6 akkor T(i,j):="C"
Elágazás vége
Csere(T(i,j),T(k,l))
Eljárás vége.
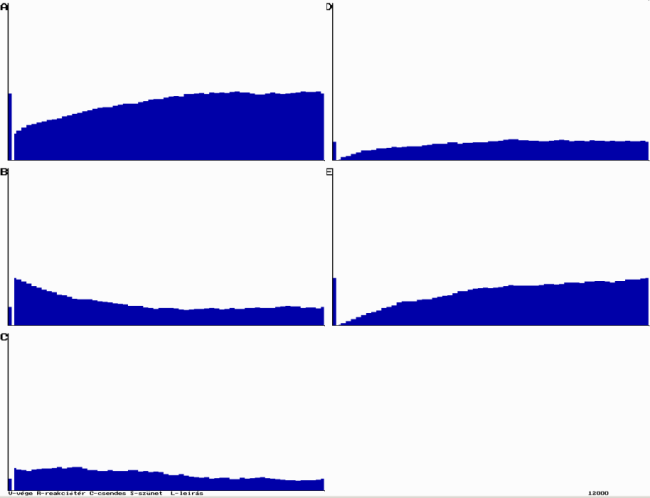
Példa az ÁT1=0,30; ÁT2=0,30; ÁT3=0,90; ÁT4=0,90; ÁT5=0,60 és ÁT6=0,60 értékére:
Az oszcillációs folyamat szimulációjaEgy igen látványos oszcilláló kémiai reakció felfedezése Briggs és Rauscher nevéhez fűződik. Kísérletükben hidrogén-peroxidot és jodátot mangánionnal egyesítenek. Ebben a reakcióban a jód és a jodidion koncentráció oszcillál, amelyet keményítővel színessé lehet tenni.
A láncreakciók olyan összetett reakciók, amelyeknél a reakcióelegyben gerjesztés (termikus, elektromos, fotokémiai, elektromágneses sugárzás) hatására meginduló startreakciókban rövid élettartamú, de a reakciósebességet igen nagy mértékben megnövelő köztitermékek – lánctagok, láncvivők – keletkeznek. Ezek a molekulák, illetve általában gyökök képesek tovább reagálni (a kiinduló anyagokkal, önmagukkal, egyéb köztitermékekkel, illetve végtermékekkel) mindaddig, amíg valamely láncletörési vagy láncvégződési reakcióban el nem fogynak vagy nem rekombinálódnak.
E folyamatok közé tartoznak a gyakorlatilag fontos égések és robbanások is. Reakciósebességük többnyire bonyolultan függ a koncentrációtól. A láncreakciós folyamat bruttó sztöchiometriai egyenlete egyszerű, de a reakció kombinált összetett típusú, mivel benne egyidejűleg mennek végbe párhuzamos, sorozatos és autokatalitikus lépések. Példa erre a HBr képződése.
A bruttó reakció:
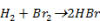
A hidrogén-bromid a következő reakcióláncban képződik:
1. | Br2 → 2Br | startreakció |
2. | Br + H2 → HBr + H | láncfolytatás |
3. | H + Br2 → HBr + Br | |
4. | H + HBr → H2 + Br | |
. | . | . |
. | . | . |
n. | 2Br → Br2 | láncletörés |
Az első lépés a Br2 molekula disszociációja, amely nagy aktiválási energiájú, tehát lassú folyamat. A 2. és 3. lépésben keletkezik egy-egy HBr molekula és egy újabb atom, amely a 2. ill. a 3. lépést újra megismételheti. A 4. reakció HBr-ot fogyaszt, de a láncot nem szakítja meg, mert újabb láncvivőt termel. Az n. reakció megszakítja a láncot, mert két láncvivőt hatástalan molekulává egyesít (lánc letörés). Ez a lépés is lassú energetikai okok miatt. A 2. és 3. lépés nagyon gyors. Ha időegység alatt ugyanannyi láncvivő keletkezik, mint amennyi elhasználódik, akkor a folyamat stacionáriussá válik.
A láncreakciók elmélete számos olyan kérdést tárgyal, amelyeket érdekes lehet szimulációs programmal vizsgálni. Például:
Láncreakció számos oxidáció, halogénezés, polimerizáció és bomlás. Igen érdekesnek tűnik elsősorban a polimerizáció és a szénhidrogének bomlása, a krakkolás, mert ezeknél a nagy méretű molekuláknál a gyökök alakja és mérete nem elhanyagolható. Szimulációs programban ennek figyelembevétele további meggondolást kíván. Például:
Nézzünk egy egyenes láncú reakciót: Jelöljük nagybetűkkel a kétatomos molekulákat, és kisbetűkkel a gyököket. Tehát A molekulán aa-t, B molekulán bb-t és C molekulán ab összetételt érthetünk.
A bruttó reakció:
B → b + b | startreakció gerjesztés hatására |
b + A → C + a | lánctag reakciók |
a + B → C + b | |
a + C → A + b | |
b + C → B + a | |
b + b → B | láncletörési reakció |
A startreakció átalakulási valószínűsége legyen ÁT1 (a valóságban kicsi, mert lassú reakció lépés), a lánctag reakciók 1 valószínűséggel menjenek végbe (igen gyors reakciók) és a letörési reakció valószínűsége legyen ÁT2.
Láncreakció:
(i,j):=véletlen hely(N,M)
(k,l):=véletlen szomszéd(i,j)
v:=véletlenszám
Elágazás
T(i,j)="A" esetén Ha T(k,l)="b" akkor T(i,j):="C"; T(k,l):="a"
T(i,j)="B" esetén Ha v<ÁT1 és Van szomszéd(i,j,k,l)
akkor T(i,j):="b"; T(k,l):="b"
T(i,j)="a" esetén Elágazás
T(k,l)="B" esetén T(i,j):="C"; T(k,l):="b"
T(k,l)="C" esetén T(i,j):="A"; T(k,l):="b"
Elágazás vége
T(i,j)="b" esetén Elágazás
T(k,l)="A" esetén T(i,j):="C"; T(k,l):="a"
T(k,l)="C" esetén T(i,j):="B"; T(k,l):="a"
T(k,l)="b" esetén Ha v<ÁT2 akkor T(i,j):="B"
T(k,l):=" "
Elágazás vége
Elágazás vége
Csere(T(i,j),T(k,l))
Eljárás vége.
A szimulációt érdemes csak A és B molekulák jelenlétével kezdeni, ÁT1 és ÁT2 arányát különböző esetekben kipróbálni. Ilyen típusú reakció pl. a fotokémiai gerjesztésű H2 + Cl2 = 2HCl (klór durranógáz) és a termikus gerjesztésű H2 + Br2 = 2HBr reakció.
 |
 |
 |
| Készült az "Országos koordinációval a pedagógusképzés megújításáért” című TÁMOP-4.1.2.B.2-13/1-2013-0007 pályázat keretében. (ISBN 978-963-284-631-6) | ||
A tananyag az ELTESCORM keretrendszerrel készült