Egy modellcsaládot fogunk létrehozni. Először megalkotjuk a család ősmodelljét. Mindegyik modellben alapvető szerepe lesz annak, hogy a különböző egyedek találkozzanak egymással (szomszédság), így a szimulációt egy N×M-es mezőn fogjuk lejátszani (használunk egy T(N,M) táblázatot). Ezen a mezőn betűk fogják jelölni az egyes egyedeket. A modellcsaládnál a folytonos keretmodellt fogjuk használni (kiegészítve a folytonos diffúziós modellel). Ehhez önkényesen választottunk egy elemi időegységet. Így a szimulációs lépés az önkényesen kiválasztott év eseményeinek lejátszását tartalmazza.
Éves változás:
Ciklus t=1-től T0-ig
(i,j):=véletlen hely(N,M)
Változás(i,j)
Mozgás(i,j)
Ciklus vége
Eljárás vége.
Változás(i,j):
Elágazás
T(i,j) állat esetén Állat változása
T(i,j) növény esetén Növény változása
T(i,j) üres esetén Növény születése
Elágazás vége
Eljárás vége.
A változás születést, halálozást, egymás megevését jelenti, a mozgás pedig az egyedek – esetleg korlátozott, különböző mértékű – helyváltoztatása. Az egyes modelleknél ezeket az eljárásokat fogjuk megírni.
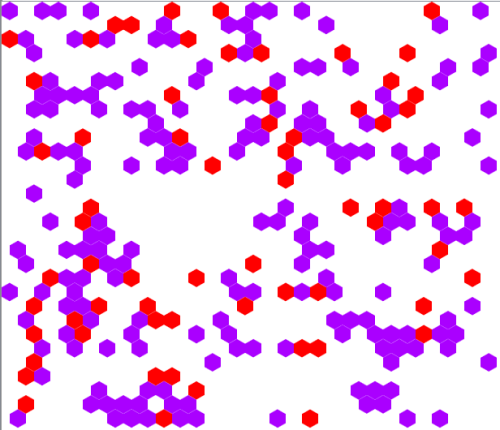 Zsákmányszerzés: rókák és nyulak.
Zsákmányszerzés: rókák és nyulak.A modellcsaládban néhány, a valós rendszer lehetőségeit szűkítő feltételt veszünk figyelembe. Ezek a következők:
1. Időfüggetlen egyedi lét (nincs korlát az életkorra).
2. Adott eloszlású élettartam.
3. Születéstől a halálig teljes kifejlettség (a paraméterek korfüggetlenek).
4. Homogén fajok (nincs szelekciós különbség).
5. A nemeket nem különböztetjük meg, a születéshez egy egyed elegendő.
6. Irányítatlan mozgás (egymás elhelyezkedését nem veszik figyelembe, nincs csoportos viselkedés, menekülés, üldözés stb.).
7. Az egyéb külső erőket csak statisztikus hatásuk eredőjével vesszük figyelembe (paramétereken keresztül).
8. A születés-halálozás a táplálkozáshoz képest erősen felgyorsított, így csak az egyes fajok saját maguk korábbi létszámához viszonyított változása értékelhető.
9. A táplálkozás a mozgáshoz képest erősen felgyorsított.
10. Egyszerre csak egy utód születhet.
Először olyan kölcsönhatástípusokkal foglalkozunk, amelyekben (két faj esetén) az egyik faj a másikra pozitív, a másik az egyikre pedig negatív hatást gyakorol. Ez a hatás táplálkozási kapcsolaton keresztül érvényesül. Első közelítésben két alapesettel foglalkozunk: az állatok állatok általi megevésével (ragadozás) és a növényevéssel. Matematikai (analitikus) modellek megalkotásakor ezeket általában nem különböztetik meg, noha a bonyolultabb modelleknél ez már szükségessé válik. Mi ezt a megkülönböztetést szimulációs módszerünk miatt – a természeti jelenség közvetlen lejátszása – már a kezdet kezdetén megtesszük.
Vizsgáljuk két állatfaj (ragadozó, zsákmány) egyedszámának egymásra hatását, a ragadozó csupán az egyetlen zsákmány faj egyedeiből él, a zsákmány szaporodását pedig a maximális élettéren kívül más tényező nem befolyásolja (minden egyéb hatást a zsákmány egyedi halálozási rátájában vettünk figyelembe). A modellben megadjuk mindkét fajta egyed szaporodásának, illetve halálozásának szabályait, továbbá egymásra hatásukat:
Mindkét faj exponenciális növekedésű, ezért változásaikat a létszámukkal arányosan kell elvégezni:
Szimulációs lépés:
(i,j):=véletlen hely(N,M)
Elágazás
T(i,j)="R" esetén Ragadozó változása(i,j)
T(i,j)="Z" esetén Zsákmány változása(i,j)
Elágazás vége
Mozgás
Eljárás vége.
A ragadozó két ok miatt halhat meg: vagy éhen hal, vagy pedig más ok miatt hal meg (ezt a ragadozó halálozási rátájában vettük figyelembe). Ha nem hal meg, akkor RS valószínűséggel szaporodik, s a szaporodástól függetlenül megeszik egyet a zsákmány szomszédjai közül.
Ragadozó változása(i,j):
Szomszédkeresés("Z",VAN,si,sj)
Ha nem VAN vagy véletlenszám<RH akkor
T(i,j):=" "
különben
Ha véletlenszám<RS akkor T(si,sj):="R"
különben T(si,sj):=" "
Elágazás vége
Eljárás vége.
A zsákmányállat ZH valószínűséggel hal meg, utódja pedig szomszédos üres helyre születhet. Ha ilyen nincs, akkor születés nem lehetséges.
Zsákmány változása(i,j):
Ha véletlenszám<ZH akkor
T(i,j):=" "
különben
Szomszédkeresés(" ",VAN,si,sj)
Ha VAN és véletlenszám<ZS akkor T(si,sj):="Z"
Elágazás vége
Eljárás vége.
A mozgás a legegyszerűbb esetben egy véletlen szomszédválasztást, s a szomszéddal való cserét jelenti.
Mozgás(i,j):
(k,l):=véletlen szomszéd(i,j)
Csere(T(i,j),T(k,l))
Eljárás vége.
A modell használata során megfigyelhetjük, hogy nagyon sok esetben a két populáció egyedszáma periodikusan ingadozik. Az egyik populáció valamilyen késéssel követi a másikat – ha sok zsákmány van, akkor a ragadozók száma növekedni kezd, de ettől előbb-utóbb csökkeni fog a zsákmány egyedszáma. Ennek viszont egy idő után az a hatása, hogy a ragadozók száma is csökkeni kezd, s ha a ragadozók száma eléggé lefogyott, akkor újra növekszik a zsákmányállatok száma. Ezt a problémát matematikai eszközökkel az ún. Lotka-Volterra egyenletekkel szokták leírni.
Az alábbi differenciálegyenletekkel definiálják a Lotka-Volterra egyenleteket:
dH/dt = rH - aPH
dP/dt = bPH - mP
Jelölések:
H(t) – a zsákmánypopuláció létszáma a t időpillanatban,
P(t) – a ragadozópopuláció létszáma a t időpillanatban,
dH/dt – a zsákmánypopuláció létszámváltozás függvénye, azaz a H(t) függvény t-szerinti deriváltja,
dP/dt – a ragadozópopuláció létszámváltozás függvénye, azaz a P(t) függvény t-szerinti deriváltja.
Az r , a , b és m időtől nem függő paraméterek.
Az egyenletek megoldását adott kezdőértékek mellett keressük:
H(0)=H0
P(0)=P0
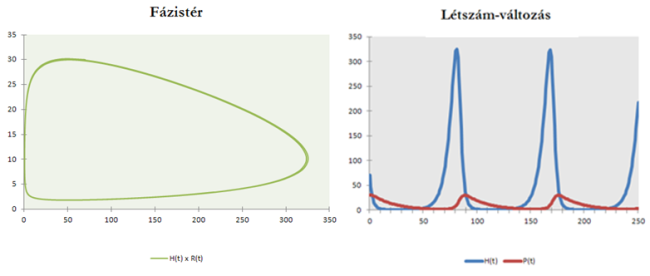 A Lotka-Volterra egyenletek „működése” (r=0,2; a=0,02; b=0,001; m=0,05; H(0)=70; P(0)=30).
A Lotka-Volterra egyenletek „működése” (r=0,2; a=0,02; b=0,001; m=0,05; H(0)=70; P(0)=30).Ha mindkét faj kezdeti létszámát arányosan csökkentjük, akkor ez elég hosszú időn át a zsákmány szaporodásának fog kedvezni (Volterra-elv).
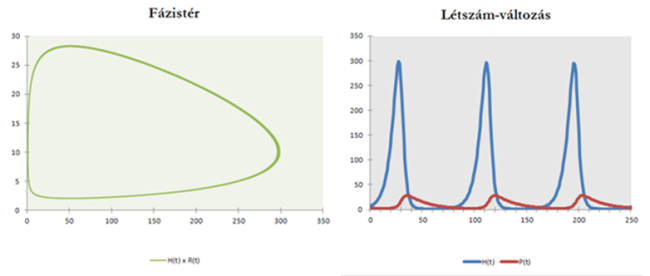 A Volterra-elv (r=0,2; a=0,02; b=0,001; m=0,05; H(0)=7; P(0)=3).
A Volterra-elv (r=0,2; a=0,02; b=0,001; m=0,05; H(0)=7; P(0)=3).A ragadozók létszámára káros hatású (túl lassú szaporodás és túl gyors halálozás esetén kívül), ha kevés és lassan szaporodó zsákmány van (kihal vagy nagy ingadozás, alacsony egyedszám stb.).
Ha mindkét populáció gyorsan szaporodik, az erős instabilitást eredményez.
Maximális szaporodási rátájától mindkét faj jelentősen elmarad (ennek oka a táplálkozási kapcsolat).
Vizsgáljuk most egy növény és egy ezt fogyasztó állatfaj létszámának alakulását, ha más erő nem hat rájuk! Az egymásra hatást és a születés-halálozás szabályait adjuk meg ebben az esetben is.
Felmerül azonban néhány probléma, amelyeket az előző modell alapján nem tudunk megoldani, más megoldást kell keresni. Ezek a következők:
A mozgás megoldására nagyon bonyolult eljárást kellene írnunk, ezért más úton fogunk járni. A vizsgált teret bontsuk fel két síkra! Az egyikben élnek a növények, a másikban pedig az állatok. A növények táblázata legyen NT(N,M) , az állatoké pedig AT(N,M) ! Ekkor mozgás természetesen csak az AT() táblázatban történik. Ezzel az első két problémát egyszerűen megoldhatjuk. A másik kettő megoldásához a növényből vezessünk be kétfajtát: N legyen a teljesen kifejlett növény, n pedig a – lelegelt, elszáradt – nem teljesen kifejlett növény!
Szimulációs lépés:
(i,j):=véletlen hely(N,M)
Ha AT(i,j)="A" akkor Növényevő változása(i,j)
Elágazás
NT(i,j)="N" esetén Növény változása(i,j)
NT(i,j)="n" esetén Kis növény változása(i,j)
NT(i,j)=" " esetén Növény születése(i,j)
Elágazás vége
Mozgás(i,j)
Eljárás vége.
Növényevő változása(i,j):
Szomszédkeresés(NT(),"N",VAN,si,sj)
Ha nem VAN vagy véletlenszám<AH akkor
AT(i,j):=" "
különben
NT(si,sj):="n"
Szomszédkeresés(AT()," ",VAN,si,sj)
Ha VAN és véletlenszám<AS akkor AT(si,sj):="A"
Elágazás vége
Eljárás vége.
A növény kétféleképpen pusztulhat ki, a teljes kipusztulás NH valószínűséggel történik, az elszáradás pedig NE valószínűséggel.
Növény változása(i,j):
Ha véletlenszám<NH akkor NT(i,j):=" "
különben Ha véletlenszám<NE akkor NT(i,j):="n"
Eljárás vége.
A kis növény minden esetben növekszik, de NH valószínűséggel ő is kipusztulhat.
Kis növény változása(i,j):
Ha véletlenszám<NH akkor NT(i,j):=" " különben NT(i,j):="N"
Eljárás vége.
A növény születésénél már figyelembe vettük, hogy üres helyen nőhet új növény. Itt csak akkor engedjük meg ezt, ha a szomszédságban van már növény, ami a magjait ide elszórhatja.
Növény születése(i,j):
Szomszédkeresés(NT(),"N",VAN,si,sj)
Ha VAN és véletlenszám<NS akkor AT(i,j):="n"
Eljárás vége.
A modell használata során megállapíthatjuk, hogy a növényevés hatása – mint vártuk – hasonló a ragadozáshoz, bár itt könnyebb stabilitásra vezető paramétereket megadni (ennek oka a növények lényegesen gyorsabb növekedése). A populációk egyensúlyi arányát és stabilitását nagymértékben befolyásolja az állatok táplálékigénye.
Ezután populációk versengésével, szimbiózisával, általában olyan kapcsolatával foglalkozunk, amelyben a populációk között közvetlen – táplálkozási – kapcsolat nincs, csupán közvetve hatnak egymásra. Először állatokkal, azután pedig növényekkel foglalkozunk.
Vizsgáljunk két fajt (A, B-betűk)! Egy időegység alatt minden egyedüknek AS , illetve BS valószínűséggel születik utódja; AH , illetve BH valószínűséggel hal meg (az öregségtől, betegségtől stb.). Minden egyednek a környezetében AK , illetve BK mennyiségű táplálékra van szüksége. Ha a szomszéd állatok annyit megesznek, hogy nem marad ennyi, akkor ez az egyed meghal (az éhségtől). Háromféle táplálékot feltételezünk (bár ezek változását nem vizsgáljuk, feltesszük, hogy a mennyiségük a megfelelő ütemben pótlódik):
Mindkét faj kétféle táplálékot fogyaszt, ezek mennyiségét kell meghatároznunk. A szomszédos 'A'-k AA , a 'B'-k pedig BA mennyiségű táplálékot fogyasztanak el az 'A'-k által fogyasztott táplálékból. Ugyanez a 'B'-kre AB , illetve BB . A rendelkezésre álló összes táplálékmennyiség OM .
Az adatábrázolásban a modellcsalád alapváltozatához térünk vissza, a T(N,M) táblázatban A-, B-betűk, illetve üres helyek lesznek.
Modellünkben a szimulációs lépést a következő algoritmussal valósítjuk meg:
Szimulációs lépés:
(i,j):=véletlen hely(N,M)
Szomszédszámlálás(i,j,"A",sa)
Szomszédszámlálás(i,j,"B",sb)
Elágazás
T(i,j)="A" esetén A-faj változása(i,j,sa,sb)
T(i,j)="B" esetén B-faj változása(i,j,sa,sb)
Elágazás vége
Mozgás(i,j)
Eljárás vége.
A két faj változását, mivel egyenrangúak, nagyon hasonlóan fogjuk elkészíteni:
A-faj változása(i,j,sa,sb):
Ha OM-(AA*sa+BA*sb)<AK vagy véletlenszám<AH akkor
T(i,j):=" "
különben
Szomszédkeresés(VAN," ",si,sj)
Ha VAN és véletlenszám<AS akkor T(si,sj):="A"
Elágazás vége
Eljárás vége.
B-faj változása(i,j,sa,sb):
Ha OM-(AB*sa+BB*sb)<BK vagy véletlenszám<BH akkor
T(i,j):=" "
különben
Szomszédkeresés(VAN," ",si,sj)
Ha VAN és véletlenszám<BS akkor T(si,sj):="B"
Elágazás vége
Eljárás vége.
A mozgás megegyezik a ragadozás esetén leírt mozgással.
Mozgás(i,j):
(k,l):=véletlen szomszéd(i,j)
Csere(T(i,j),T(k,l))
Eljárás vége.
A két populáció egymásra hatását a BA és az AB paraméterekkel befolyásolhatjuk. Amikor mindkettő pozitív értékű, akkor a két faj versengéséről beszélhetünk (fiktív példa: őzek és szarvasok). Ekkor a két populáció sorsát a fenti paraméterek nagysága, pontosabban AA -hoz és BB -hez való viszonya határozza meg. Alapvetően 3 eset fordulhat elő (emlékeztetünk az elemi modellek 3-féle típuseredményére, amely az (S+,S+) modell esetén előfordulhat):
A: stabil egyensúlyi állapot alakul ki,
B: az egyik populáció (előbb-utóbb) kihal,
B1: az első populáció biztosan kipusztul,
B2: a második populáció biztosan kipusztul,
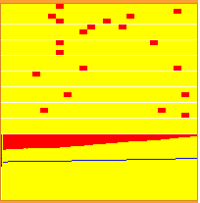 A populáció kipusztulása, versengés során.
A populáció kipusztulása, versengés során.B3: a véletlentől és a kezdőeloszlástól függ, hogy melyik populáció hal ki,
C: a két populáció aránya teljesen véletlenszerűen változik.
 A szimuláció során kialakuló populáció-létszám arányok véletlenszerűen változnak.
A szimuláció során kialakuló populáció-létszám arányok véletlenszerűen változnak.Ha a saját populáció erősebben korlátozza a létszámot, mint a másik ( BA « AA , BB « AB ), akkor alakul ki stabilitás.
Ezután nézzük meg azt az esetet, amikor BA =0 és AB <0! Ekkor az egyik populációra a másik nincs hatással, míg a másikra az egyiknek pozitív hatása van (fiktív példa: oroszlán-sakál, kommenzalizmus). Ez a kapcsolattípus lehetővé teszi, hogy a „kisegített” populáció egyensúlyi létszámát tartósan meghaladja.
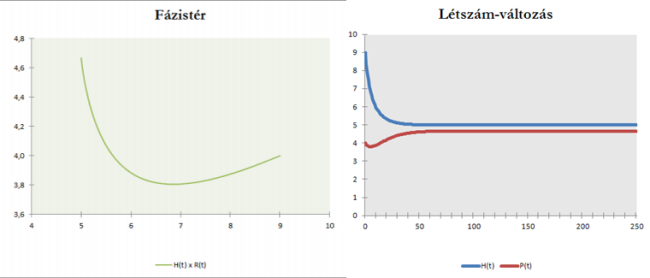 Stabil létszámok. Kommenzalizmus
Stabil létszámok. KommenzalizmusFoglalkozzunk most növények együttélésével! Előző modellünkből ebben az esetben el kell hagynunk a mozgást. A modell objektumai, paraméterei megegyeznek az előző modell objektumaival, paramétereivel. Természetesen ebben a modellben mozgás nem lesz.
Szimulációs lépés:
(i,j):=véletlen hely(N,M)
Szomszédszámlálás(i,j,"A",sa)
Szomszédszámlálás(i,j,"B",sb)
Elágazás
T(i,j)="A" esetén A-faj pusztulása(i,j,sa,sb)
T(i,j)="B" esetén B-faj pusztulása(i,j,sa,sb)
T(i,j)=" " és sa+sb>0 esetén Szaporodás(i,j,sa,sb)
Elágazás vége
Eljárás vége.
Szaporodásnál el kell dönteni, hogy melyik növény szaporodjon (ez függ a szomszédos növények számától), majd pedig azt, hogy ha szaporodhat, akkor ténylegesen szaporodik-e (pl. kikel-e a mag?).
Szaporodás(i,j,sa,sb):
Ha véletlenszám<sa/(sa+sb) akkor
Ha véletlenszám<AS akkor T(i,j):="A"
különben
Ha véletlenszám<BS akkor T(i,j):="B"
Elágazás vége
Eljárás vége.
A kipusztulás két ok miatt következhet be:
A-faj pusztulása(i,j,sa,sb):
Ha OM-(AA*sa+BA*sb)<AK vagy véletlenszám<AH akkor T(i,j):=" "
Eljárás vége.
B-faj pusztulása(i,j,sa,sb):
Ha OM-(AB*sa+BB*sb)<BK vagy véletlenszám<BH akkor T(i,j):=" "
Eljárás vége.
Amennyiben BA és AB pozitív, úgy most is egy versengési problémát vizsgálhatunk, s megállapíthatjuk, hogy az állatok esetén tapasztalt jelenségek itt is fellépnek, ezt a mozgás hiánya nem változtatja meg.
Érdekes a BA=0 , AB>0 eset (fiktív példa: fa-fénykedvelő virág, amenzalizmus). Ekkor az egyik faj megakadályozza a másik növekedését, amely csak úgy tud fennmaradni, ha nagyon gyors ütemben képes szaporodni, s az első faj önmagát is eléggé korlátozza.
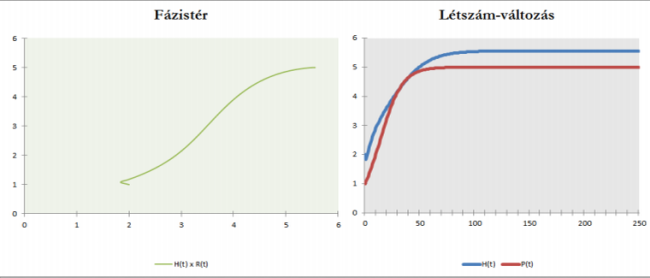 Stabil létszámok. Amenzalizmus.
Stabil létszámok. Amenzalizmus.További példa, amikor BA és AB is negatív: mindkettő segíti a másik növekedését (szimbiózis). Ezzel a normális egyensúlyi létszámnál magasabb létszámot érhet el mindkét populáció.
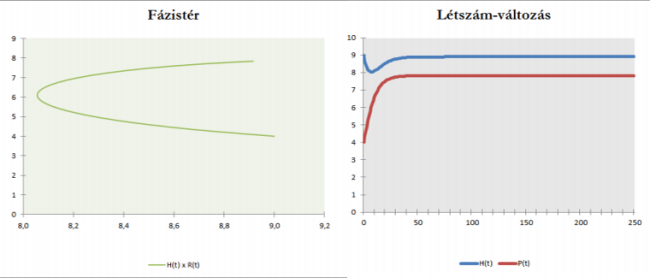 Stabil létszámok. Szimbiózis.
Stabil létszámok. Szimbiózis.Megfontolásra ajánljuk Olvasóinknak a csoportosan élő állatok (pl. hangyák, méhek, ...) táplálékszerzésével, szaporodásával kapcsolatos modellezési lehetőségeket!
 |
 |
 |
| Készült az "Országos koordinációval a pedagógusképzés megújításáért” című TÁMOP-4.1.2.B.2-13/1-2013-0007 pályázat keretében. (ISBN 978-963-284-631-6) | ||
A tananyag az ELTESCORM keretrendszerrel készült