Halmazműveletek
Ha e műveleteket alkalmazzuk, akkor a relációkra néhány feltételnek teljesülnie kell:
- Az R és S relációk sémájának ugyanazokat az attribútumhalmazokat kell tartalmaznia.
- Az R és S relációk oszlopait rendezni kell úgy, hogy az R reláció i-edik attribútumának a neve
megegyezzen az S reláció i-edik attribútumával, vagyis az attribútumok sorrendje azonos legyen mindkét reláció esetén.
Unió
R S, azon sorok halmaza, amelyek
vagy az R-ben, vagy az S-ben vannak. Egy elem csak egyszer szerepel az egyesítésben, még akkor is,
ha jelen van az R-ben is és az S-ben is.
S, azon sorok halmaza, amelyek
vagy az R-ben, vagy az S-ben vannak. Egy elem csak egyszer szerepel az egyesítésben, még akkor is,
ha jelen van az R-ben is és az S-ben is.
R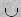 S:
S:
| A
| B
|
| 1
| 4
|
| 2
| 5
|
| 3
| 6
|
| 6
| 2
|
| 7
| 9
|
Metszet (Intersection)
R S, R és S metszete azon sorok halmaza, amelyek az R-ben is és az S-ben is benne vannak.
S, R és S metszete azon sorok halmaza, amelyek az R-ben is és az S-ben is benne vannak.
R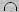 S:
S:
| A
| B
|
| 2
| 5
|
Különbség (Difference)
R-S, R és S különbsége azon sorok halmaza, melyek benne vannak R-ben, de nincsenek benne S-ben.
Megjegyzendő, hogy R-S nem ugyanaz, mint S-R, mivel ez utóbbi azon sorok halmaza, melyek benne vannak S-ben,
de nincsenek R-ben.
Megjegyzés:
A metszet kifejezhető a különbség művelet segítségével.
R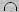 S= R – (R – S)
S= R – (R – S)
Tehát, ha R és S két, azonos sémával rendelkező reláció, akkor R és S metszete (R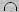 S)
kiszámolható úgy, hogy először kiszámoljuk a T relációt, amelyben mindazok a sorok benne
vannak, amelyek benne vannak R-ben is, de S-nek nem sorai, azaz kivonjuk az R-ből az S relációt.
Ezután kivonjuk az R-ből a T relációt, ezáltal R-nek azokat a sorait kapjuk, amelyek S-ben
is benne vannak, tehát megkapjuk R és S metszetét.
S)
kiszámolható úgy, hogy először kiszámoljuk a T relációt, amelyben mindazok a sorok benne
vannak, amelyek benne vannak R-ben is, de S-nek nem sorai, azaz kivonjuk az R-ből az S relációt.
Ezután kivonjuk az R-ből a T relációt, ezáltal R-nek azokat a sorait kapjuk, amelyek S-ben
is benne vannak, tehát megkapjuk R és S metszetét.
Példa:

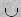 S:
S: S, azon sorok halmaza, amelyek
vagy az R-ben, vagy az S-ben vannak. Egy elem csak egyszer szerepel az egyesítésben, még akkor is,
ha jelen van az R-ben is és az S-ben is.
S, azon sorok halmaza, amelyek
vagy az R-ben, vagy az S-ben vannak. Egy elem csak egyszer szerepel az egyesítésben, még akkor is,
ha jelen van az R-ben is és az S-ben is.
 S, R és S metszete azon sorok halmaza, amelyek az R-ben is és az S-ben is benne vannak.
S, R és S metszete azon sorok halmaza, amelyek az R-ben is és az S-ben is benne vannak.
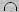 S= R – (R – S)
S= R – (R – S)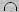 S)
kiszámolható úgy, hogy először kiszámoljuk a T relációt, amelyben mindazok a sorok benne
vannak, amelyek benne vannak R-ben is, de S-nek nem sorai, azaz kivonjuk az R-ből az S relációt.
Ezután kivonjuk az R-ből a T relációt, ezáltal R-nek azokat a sorait kapjuk, amelyek S-ben
is benne vannak, tehát megkapjuk R és S metszetét.
S)
kiszámolható úgy, hogy először kiszámoljuk a T relációt, amelyben mindazok a sorok benne
vannak, amelyek benne vannak R-ben is, de S-nek nem sorai, azaz kivonjuk az R-ből az S relációt.
Ezután kivonjuk az R-ből a T relációt, ezáltal R-nek azokat a sorait kapjuk, amelyek S-ben
is benne vannak, tehát megkapjuk R és S metszetét.
