Természetes összekapcsolás (natural join)
Két reláció szorzásánál gyakrabban van szükségünk arra, hogy összekapcsoljunk relációkat
oly módon, hogy csak azokat párosítjuk, amelyek valamilyen módon összeillenek. Az összeillesztés
legegyszerűbb módja két reláció természetes összekapcsolása.
Az R és az S relációk természetes
összekapcsolását az R S kifejezéssel jelöljük.
S kifejezéssel jelöljük.
E művelet használatával R és S relációknak csak azokat a sorait párosítjuk össze, amelyek értékei megegyeznek az R és az S sémájának összes
közös attribútumán. Pontosabban definiálva: legyenek A1, A2, …, An azok az attribútumok, amelyek
megtalálhatók mind az R, mind pedig az S sémájában. Ekkor az R egy r sorának és S egy s sorának
párosítása akkor és csak akkor sikeres, ha az r és az s megfelelő értékei megegyeznek az összes
A1, A2, …, An attribútumon.
Ha az r és s sorok párosítása az R S összekapcsolásban sikeres, akkor a párosítás
eredménye egy olyan, összekapcsolt sornak nevezett sor, amelyben az R és S sémájának egyesítésében
szereplő összes attribútumhoz egyetlen komponens tartozik. Az összekapcsolt sor megegyezik az r
sorral az R reláció összes attribútumán, és megegyezik az s sorral az S reláció összes
attribútumán. Mivel az r és s összekapcsolása sikeres volt, így tudjuk, hogy az r és s
megegyezik azokon az attribútumokon, amelyek mind az R, mind pedig az S sémájában szerepelnek.
Ezért az összekapcsolt sor is megegyezik mind az r, mind az s sorokkal a mindkét sémában szereplő
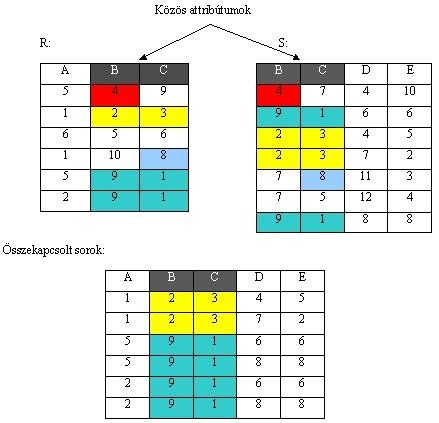
attribútumokon. Az összekapcsolt sor szerkezetét az alábbi ábra szemlélteti (az egyenlő értékek
a közös attribútumukon azonos színnel vannak jelölve) :
S összekapcsolásban sikeres, akkor a párosítás
eredménye egy olyan, összekapcsolt sornak nevezett sor, amelyben az R és S sémájának egyesítésében
szereplő összes attribútumhoz egyetlen komponens tartozik. Az összekapcsolt sor megegyezik az r
sorral az R reláció összes attribútumán, és megegyezik az s sorral az S reláció összes
attribútumán. Mivel az r és s összekapcsolása sikeres volt, így tudjuk, hogy az r és s
megegyezik azokon az attribútumokon, amelyek mind az R, mind pedig az S sémájában szerepelnek.
Ezért az összekapcsolt sor is megegyezik mind az r, mind az s sorokkal a mindkét sémában szereplő
attribútumokon. Az összekapcsolt sor szerkezetét az alábbi ábra szemlélteti (az egyenlő értékek
a közös attribútumukon azonos színnel vannak jelölve) :
1.Példa:
S:
| B
| C
| D
|
| 4
| 3
| 5
|
| 5
| 10
| 2
|
| 8
| 4
| 9
|
R S:
S:
| A
| B
| C
| D
|
| 1
| 4
| 3
| 5
|
| 2
| 5
| 10
| 2
|
Ebben a példában az R és S egyetlen közös attribútuma a B. Az R reláció első sora csak az S
első sorával párosítható sikeresen. Mindkét sor B attribútumának értéke ekkor „2”. Ez a párosítás
lesz az eredményreláció első sora (1, 4, 3, 5). Az R reláció második sora is S relációnak csak
egyik sorával párosítható össze. Ebből kapjuk az eredményreláció második sorát (2, 5, 10, 2).
Megjegyzendő, hogy az S harmadik sorát nem lehet párosítani R egyik sorával sem, ezért nincs is
semmilyen hatása az R S művelet eredményére nézve. Az ilyen sort, amelyet nem lehet sikeresen
párosítani az összekapcsolásban szereplő másik reláció egyetlen sorával sem, lógó sornak is
nevezzük.
S művelet eredményére nézve. Az ilyen sort, amelyet nem lehet sikeresen
párosítani az összekapcsolásban szereplő másik reláció egyetlen sorával sem, lógó sornak is
nevezzük.
2.Példa:
Most nézzünk olyan példát is, amelyben van olyan sor, amelyik egynél több sorral is párosítható
, és ahol a két reláció sémájának nem egy közös attribútuma van. A következő relációkra
ezek a feltételek teljesülnek, mivel az R első sora sikeresen párosítható az S első két sorával
(az S relációnak harmadik sora az R reláció második és harmadik sorával) és a relációknak két
közös attribútumuk (B és C) is van, melyek komponenseinek egyezni kell.
R:
| A
| B
| C
|
| 1
| 4
| 6
|
| 4
| 7
| 9
|
| 2
| 7
| 9
|
S:
| B
| C
| D
|
| 4
| 6
| 3
|
| 4
| 6
| 2
|
| 7
| 9
| 13
|
R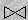 S:
S:
| A
| B
| C
| D
|
| 1
| 4
| 6
| 3
|
| 1
| 4
| 6
| 2
|
| 4
| 7
| 9
| 13
|
| 2
| 7
| 9
| 13
|
Megjegyzés:
A természetes összekapcsolás kifejezhető más műveletek segítségével, mégpedig ezek a szorzás,
kiválasztás és vetítés :
R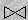 S = πL(σC(R×S))
S = πL(σC(R×S))
ahol C feltétel R.A1 = S.A1 AND R.A2 = S.A2 AND … AND R.An = S.An alakú és az
A1, A2, … , An olyan attribútumok, amelyek mind az R, mind az S sémájában szerepelnek,
tehát R séma 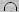 S séma = {A1, A2, …, An}.
S séma = {A1, A2, …, An}.
Az L pedig egy olyan attribútumlista, amelyben szerepel az R összes attribútuma és emellett
az S-ből mindazok az attribútumok, amelyek nincsenek benne az R reláció sémájában, tehát
L = R séma + (S séma – R séma) .
3.Példa
1.lépés:
Az R és S relációk természetes összekapcsolásának kifejezéséhez először vegyük az R×S Descartes – szorzatot:
S:
| B
| C
| D
|
| 4
| 3
| 5
|
| 4
| 10
| 2
|
| 8
| 4
| 9
|
R×S:
| A
| R.B
| R.C
| S.B
| S.C
| D
|
| 1
| 4
| 3
| 4
| 3
| 5
|
| 1
| 4
| 3
| 4
| 10
| 2
|
| 1
| 4
| 3
| 8
| 4
| 9
|
| 2
| 8
| 4
| 4
| 3
| 5
|
| 2
| 8
| 4
| 4
| 10
| 2
|
| 2
| 8
| 4
| 8
| 4
| 9
|
2.lépés:
Alkalmazzuk a kiválasztás operátort.
Ki kell választani azokat a sorokat, amelyek a feltétel szerint, mind az R.B – S.B és mind az R.C – S.C attribútumpárokon azonos értékekkel rendelkeznek. Ekkor a részeredmény:
| A
| R.B
| R.C
| S.B
| S.C
| D
|
| 1
| 4
| 3
| 4
| 3
| 5
|
| 2
| 8
| 4
| 8
| 4
| 9
|
3.lépés:
Utolsó lépésként pedig mindegyik közös attribútumból, vagyis a B és C attribútumokból,
csak egy példányt őrizzünk meg. Ezt az A, R.B, R.C, D attribútumokra vetítéssel tehetjük meg.
Így kapjuk meg az R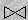 S végeredményét:
S végeredményét:
πA, R.B, R.C, D (σR.B=S.B AND R.C=S.C( R×S ) )
Végeredmény:
| A
| R.B
| R.C
| D
|
| 1
| 4
| 3
| 5
|
| 2
| 8
| 4
| 9
|

 S kifejezéssel jelöljük.
S kifejezéssel jelöljük.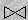 S összekapcsolásban sikeres, akkor a párosítás
eredménye egy olyan, összekapcsolt sornak nevezett sor, amelyben az R és S sémájának egyesítésében
szereplő összes attribútumhoz egyetlen komponens tartozik. Az összekapcsolt sor megegyezik az r
sorral az R reláció összes attribútumán, és megegyezik az s sorral az S reláció összes
attribútumán. Mivel az r és s összekapcsolása sikeres volt, így tudjuk, hogy az r és s
megegyezik azokon az attribútumokon, amelyek mind az R, mind pedig az S sémájában szerepelnek.
Ezért az összekapcsolt sor is megegyezik mind az r, mind az s sorokkal a mindkét sémában szereplő
attribútumokon. Az összekapcsolt sor szerkezetét az alábbi ábra szemlélteti (az egyenlő értékek
a közös attribútumukon azonos színnel vannak jelölve) :
S összekapcsolásban sikeres, akkor a párosítás
eredménye egy olyan, összekapcsolt sornak nevezett sor, amelyben az R és S sémájának egyesítésében
szereplő összes attribútumhoz egyetlen komponens tartozik. Az összekapcsolt sor megegyezik az r
sorral az R reláció összes attribútumán, és megegyezik az s sorral az S reláció összes
attribútumán. Mivel az r és s összekapcsolása sikeres volt, így tudjuk, hogy az r és s
megegyezik azokon az attribútumokon, amelyek mind az R, mind pedig az S sémájában szerepelnek.
Ezért az összekapcsolt sor is megegyezik mind az r, mind az s sorokkal a mindkét sémában szereplő
attribútumokon. Az összekapcsolt sor szerkezetét az alábbi ábra szemlélteti (az egyenlő értékek
a közös attribútumukon azonos színnel vannak jelölve) :
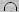 S séma = {A1, A2, …, An}.
S séma = {A1, A2, …, An}.