Théta-összekapcsolás
A természetes összekapcsolás előírja, hogy egyetlen speciális feltétel szerint párosítsuk a
sorokat, mégpedig a közös attribútumok azonos értéke alapján. Habár a relációk összekapcsolásának
leggyakoribb kiindulási pontja a közös attribútumokban lévő azonos értékek, azért néha szükség
lehet két reláció sorainak más szempontból történő párosítására, ezért vezetjük be a természetes
összekapcsolást kiterjesztve a théta – összekapcsolás műveletet.
A théta szó egy tetszőleges
feltételre utal, amit  jellel szokás jelölni.
jellel szokás jelölni.
Az egyszerűség kedvéért jelöljük most a feltételeket C-vel.
Ezek a feltételek egyszerű aritmetikai összehasonlítások, melyek C = Ai 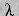 Bi alakúak, ahol a
Bi alakúak, ahol a
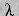
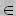 {>,<,
{>,<, ,
,  , =, ≠}.
, =, ≠}.
A théta – összekapcsolás műveletet az R S kifejezéssel jelöljük,
amely R és S relációknak C feltételre vonatkozó théta – összekapcsolása.
S kifejezéssel jelöljük,
amely R és S relációknak C feltételre vonatkozó théta – összekapcsolása.
Ennek a műveletnek az eredményét a következő lépéseket követve kaphatjuk meg:
- Kiszámoljuk R és S szorzatát.
- Kiválasztjuk a szorzatból azokat a sorokat, amelyek a C feltételnek eleget tesznek.
Az eredmény sémája, csakúgy, mint a Descartes – szorzat műveletnél, itt is az R és S relációk
sémájának egyesítése. Ha szükséges megjelölni, hogy melyik sémából származnak az attribútumok,
akkor használjuk az attribútumokhoz az „R.” illetve az „S.” előtagokat.
Vagyis ha például adott
két relációnk és azok attribútumai,
R(A, B, C, D) és S(C, D, E, F), akkor az eredmény, az előtagokat használva, a következő sémájú
lesz:
( A, B, R.C, R.D, S.C, S.D, E, F ).
1.Példa
Végezzük el az R 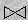 A<DS műveletet.
A<DS műveletet.
R:
| A
| B
| C
|
| 1
| 4
| 6
|
| 4
| 7
| 9
|
| 2
| 7
| 9
|
S:
| B
| C
| D
|
| 4
| 6
| 3
|
| 4
| 6
| 2
|
| 7
| 9
| 13
|
R 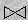 A<DS:
A<DS:
| A
| R.B
| R.C
| S.B
| S.C
| D
|
| 1
| 4
| 6
| 4
| 6
| 3
|
| 1
| 4
| 6
| 4
| 6
| 2
|
| 1
| 4
| 6
| 7
| 9
| 13
|
| 4
| 7
| 9
| 7
| 9
| 13
|
| 2
| 7
| 9
| 7
| 9
| 13
|
A két relációnak kilenc párosítása lehetséges, amelyeknek mindegyikét meg kell vizsgálni,
hogy teljesül-e rá az A<D feltétel. Az R első sora párosítva az S első sorával a következő
sort adja: (1, 4, 6, 4, 6, 5). Erre igaz lesz a feltétel, mivel 1<5. Az R első sora az S többi
sorával ugyanígy sikeresen párosítható. Az R második és harmadik sora viszont csak az S utolsó
sorával párosítva tudja teljesíteni a feltételt, mivel a többi esetben az A<D, vagyis a 4<3, 4<2,
2<3 és 2<2 hamis értéket ad a feltételre.
Ha megfigyeljük a természetes összekapcsolás és a
théta – összekapcsolás eredményeit, akkor szembe tűnik, hogy a théta-összekapcsolásnál az
attribútumok száma több. Ez annak tudható be, hogy amíg a természetes összekapcsolásban a
közös attribútumok csak egyszer szerepelnek az egyenlő értékek miatt, addig a théta –
összekapcsolásban a közös attribútumok mindegyikét megjelenítjük, és előtaggal látjuk el,
hiszen itt az értékek különbözőek is lehetnek. Ezzel az előtaggal jelezzük, hogy melyik
relációból származik az attribútum.
2.Példa
Legyen a feltételünk összetett. Végezzük el az R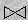 A<D AND R.C≠S.C S műveletet.
A<D AND R.C≠S.C S műveletet.
Ekkor az előző példában lévő eredményrelációra az A<D összehasonlításon kívül annak is
teljesülnie kell, hogy különbözzön az R és S relációknak a C attribútumban lévő értéke.
Ezeket a feltételeket csak egyetlen sor teljesíti, így az eredmény a következő sor lesz:
R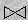 A<D AND R.C≠S.C S:
A<D AND R.C≠S.C S:
| A
| R.B
| R.C
| S.B
| S.C
| D
|
| 1
| 4
| 6
| 7
| 9
| 13
|
Megjegyzés:
A théta-összekapcsolás kifejezhető más műveletek segítségével, mégpedig ezek a szorzás és
kiválasztás:
R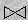 CS = σC(R×S)
CS = σC(R×S)
3.Példa
Végezzük el az 2.példát szorzással és kiválasztással.
R:
| A
| B
| C
|
| 1
| 4
| 6
|
| 4
| 7
| 9
|
| 2
| 7
| 9
|
S:
| B
| C
| D
|
| 4
| 6
| 3
|
| 4
| 6
| 2
|
| 7
| 9
| 13
|
1.lépés:
Ki kell számolni az R és S Descartes – szorzatát
R×S:
| A
| R.B
| R.C
| S.B
| S.C
| D
|
| 1
| 4
| 6
| 4
| 6
| 3
|
| 1
| 4
| 6
| 4
| 6
| 2
|
| 1
| 4
| 6
| 7
| 9
| 13
|
| 4
| 7
| 9
| 4
| 6
| 3
|
| 4
| 7
| 9
| 4
| 6
| 2
|
| 4
| 7
| 9
| 7
| 9
| 13
|
| 2
| 7
| 9
| 4
| 6
| 3
|
| 2
| 7
| 9
| 4
| 6
| 2
|
| 2
| 7
| 9
| 7
| 9
| 13
|
2.lépés:
Alkalmazni kell a kiválasztást az A<D AND R.C≠S.C feltétel szerint.
Végeredmény:
| A
| R.B
| R.C
| S.B
| S.C
| D
|
| 1
| 4
| 6
| 7
| 9
| 13
|
Mint látható, a feltétel csak egyetlen sorra teljesül, a két eredmény pedig megegyezik.

 jellel szokás jelölni.
jellel szokás jelölni.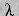 Bi alakúak, ahol a
Bi alakúak, ahol a
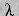
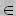 {>,<,
{>,<, ,
,  , =, ≠}.
, =, ≠}.
 S kifejezéssel jelöljük,
amely R és S relációknak C feltételre vonatkozó théta – összekapcsolása.
S kifejezéssel jelöljük,
amely R és S relációknak C feltételre vonatkozó théta – összekapcsolása.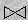 A<DS műveletet.
A<DS műveletet.
