átnevezés
Tulajdonképpen nem egy relációs algebrai művelet, hanem egy technikai dolog.
Relációs algebrai műveletek alkalmazásával újabb relációkat kapunk, és ezek neveinek
szabályozására gyakran szükség van egy olyan operátorra, amelyik kifejezetten átnevezi a
relációkat.
Egy R reláció átnevezéséhez a 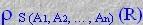 operátort használjuk.
operátort használjuk.
ρújnév <-réginév(Rel_név)
Ez azt jelenti, hogy az eredményreláció neve S lesz, sorai megegyeznek az R soraival, és
az attribútumok neve balról jobbra : A1, A2, …, An. Ha csak a reláció nevét szeretnénk
megváltoztatni és az attribútumok eredeti neveit szeretnénk megőrizni, akkor egyszerűen
csak a 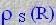 kifejezést kell használnunk.
kifejezést kell használnunk.
1. Példa
A Descartes–szorzat illusztrálásához használt példában látható két reláció ,
R és S és ezek szorzata. Megállapodtunk abban, hogyha egy attribútum mindkét operandusban
szerepel, akkor ezeket az attribútumokat átnevezzük oly módon, hogy az új névben jelenjen
meg egy előtag, amely az adott attribútumot tartalmazó reláció neve.
Ebben a példában is szintén
e két reláció, R és S található.
S:
| B
| C
| D
|
| 4
| 3
| 5
|
| 5
| 10
| 2
|
| 8
| 4
| 9
|
Tegyük fel azonban, hogy a B attribútum két előfordulását
nem R.B-vel , illetve S.B-vel szeretnénk jelölni, hanem az R reláció B attribútumának a nevét
szeretnénk megtartani, az S reláció B attribútumát pedig „X” névvel szeretnénk ellátni. E
célból átnevezhetjük az S attribútumait úgy, hogy az elsőnek a neve legyen X.
1.Megoldás: Ekkor a
ρS(X, C, D) (S) kifejezés eredménye pontosan egy olyan S nevű reláció, amelyik ugyanolyan,
mint a Descartes-szorzat példájában látható S reláció, csak az első attribútumának neve nem B, hanem X, vagyis
az S reláció attribútumai ekkor sorrendben: X, C, D . Amikor megszorozzuk az R relációt az
előbbi módon átnevezett S relációval, akkor már semmi gond sem lesz az egyforma
attribútumnevekkel, további átnevezésekre így nincsen szükség. Tehát az R ×ρS(X, C, D)(S)
kifejezés eredménye a Descartes-szorzat példájában látható R×S reláció, kivéve, hogy ekkor az öt attribútum neve
balról jobbra sorrendben a következők: A, B ,X, C, D . Tehát az eredményreláció:
R ×ρS (X, C, D)(S):
| A
| B
| X
| C
| D
|
| 1
| 4
| 4
| 3
| 5
|
| 1
| 4
| 5
| 10
| 2
|
| 1
| 4
| 8
| 4
| 9
|
| 2
| 5
| 4
| 3
| 5
|
| 2
| 5
| 5
| 10
| 2
|
| 2
| 5
| 8
| 4
| 9
|
2.Megoldás: Először kiszámoljuk a szorzatot átnevezés nélkül úgy, ahogyan
azt a Descartes–szorzat példájában is megtettük, és ezek után nevezzük át az eredményt.
Ezt a ρRS(A, B, X, C, D) (R×S) kifejezéssel tehetjük meg. Ebben az esetben az eredményreláció
attribútumai ugyanazok, mint az előző ábrán látható relációnak, csak az a különbség, hogy ekkor
az erdményreláció neve RS, míg az előző eredményrelációnak nincsen neve.
2. Példa
Az átnevezés műveletet használni kell akkor is, amikor egy relációt önmagával szorzunk, mivel
ekkor a közös attribútumok azonos előtaggal lennének kiegészítve. A következő szorzás ezt az
esetet szemlélteti.
R×R:
| R.A
| R.B
| R.C
| R.A
| R.B
| R.C
|
| 1
| 2
| 3
| 1
| 2
| 3
|
| 1
| 2
| 3
| 4
| 5
| 6
|
| 4
| 5
| 6
| 1
| 2
| 3
|
| 4
| 5
| 6
| 4
| 5
| 6
|
3. Példa
E példa azt illusztrálja, hogy miért van szükség egy reláció önmagával vett Descartes-szorzatára.
Tegyük fel, hogy a Dolgozók relációban lévő fizetések közül szeretnénk megtalálni
a legnagyobbat. Ez nem valósítható meg egyetlen lépésben, mert a relációs algebra nem biztosít
számunkra olyan változót, amelyben átmenetileg tárolni tudnánk a megtalált legnagyobb értéket.
Dolgozók reláció
| név
| adószám
| születési év
| beosztás
| fizetés
|
| Kerekes Ádám
| 3869828
| 1970
| igazgató
| 200000
|
| Szirmai Katalin
| 5745325
| 1970
| titkárnő
| 90000
|
| Binte Tamás
| 5326223
| 1964
| könyvelő
| 150000
|
Az eredményt a
πfizetés(Dolgozók)-(πDolgozók.fizetés(σDolgozók.fizetés<átnevezett.fizetés(Dolgozók×ρátnevezett(Dolgozók))))
kifejezéssel kaphatjuk meg.
1.lépés:
létre kell hozni az átnevezett nevű relációt,
amelyet a Dolgozók reláció átnevezésével érünk el, a ρátnevezett(Dolgozók) kifejezéssel.
2.lépés:
képezni kell az átnevezett relációnak a Dolgozók relációval vett Descartes – szorzatát:
| dolg. név
| dolg. adószám
| dolg. születési év
| dolg. beosztás
| dolg. fizetés
| átn. név
| átn. adószám
| átn. születési év
| átn. beosztás
| átn. fizetés
|
| Kerekes Ádám
| 3869828
| 1970
| igazgató
| 200000
| Kerekes Ádám
| 3869828
| 1970
| igazgató
| 200000
|
| Kerekes Ádám
| 3869828
| 1970
| igazgató
| 200000
| Szirmai Katalin
| 5745325
| 1970
| titkárnő
| 90000
|
| Kerekes Ádám
| 3869828
| 1970
| igazgató
| 200000
| Binte Tamás
| 5326223
| 1964
| könyvelő
| 150000
|
| Szirmai Katalin
| 5745325
| 1970
| titkárnő
| 90000
| Kerekes Ádám
| 3869828
| 1970
| igazgató
| 200000
|
| Szirmai Katalin
| 5745325
| 1970
| titkárnő
| 90000
| Szirmai Katalin
| 5745325
| 1970
| titkárnő
| 90000
|
| Szirmai Katalin
| 5745325
| 1970
| titkárnő
| 90000
| Binte Tamás
| 5326223
| 1964
| könyvelő
| 150000
|
| Binte Tamás
| 5326223
| 1964
| könyvelő
| 150000
| Kerekes Ádám
| 3869828
| 1970
| igazgató
| 200000
|
| Binte Tamás
| 5326223
| 1964
| könyvelő
| 150000
| Szirmai Katalin
| 5745325
| 1970
| titkárnő
| 90000
|
| Binte Tamás
| 5326223
| 1964
| könyvelő
| 150000
| Binte Tamás
| 5326223
| 1964
| könyvelő
| 150000
|
3.lépés:
ki kell választani azokat a sorokat, ahol a
Dolgozók.fizetés<átnevezett.fizetés feltétel teljesül. Ezek a következő sorok lesznek:
| dolg. név
| dolg. adószám
| dolg. születési év
| dolg. beosztás
| dolg. fizetés
| átn. név
| átn. adószám
| átn. születési év
| átn. beosztás
| átn. fizetés
|
| Szirmai Katalin
| 5745325
| 1970
| titkárnő
| 90000
| Kerekes Ádám
| 3869828
| 1970
| igazgató
| 200000
|
| Szirmai Katalin
| 5745325
| 1970
| titkárnő
| 90000
| Binte Tamás
| 5326223
| 1964
| könyvelő
| 150000
|
| Binte Tamás
| 5326223
| 1964
| könyvelő
| 150000
| Kerekes Ádám
| 3869828
| 1970
| igazgató
| 200000
|
4.lépés:
Ezt a relációt le kell vetíteni a Dolgozók.fizetés attribútumra. Ekkor megkapjuk a kivonandó relációt:
kivonandó
| dolg.fizetés
|
| 90000
|
| 150000
|
5.lépés:
Végül a 4.lépés részeredményét kell kivonni a Dolgozók reláció fizetés attribútumára vett
vetítéséből, ami a πfizetés(Dolgozók).
πfizetés(Dolgozók)
| dolgozók.fizetés
|
| 200000
|
| 90000
|
| 150000
|
kivonandó
| dolgozók.fizetés
|
| 90000
|
| 150000
|
Végeredmény:

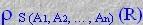 operátort használjuk.
operátort használjuk.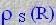 kifejezést kell használnunk.
kifejezést kell használnunk.