Egymintás u-próba

A Wikipédiából, a szabad lexikonból.

Az egymintás u-próba (más néven egymintás z-próba) a statiszitkai hipotézisvizsgálatok közül a paraméteres próbák közé tartozik. A próba azt ellenőrzi, hogy egy adott statisztikai ismérv esetén a mintabeli átlag szignifikánsan eltér-e a populációs átlagtól. Más szavakkal, hogy egy valószínűségi változó átlaga szignifikánsan különbözik-e egy adott m értéktől.

Az u-próbáról általában lásd még: u-próba.

Tartalomjegyzék

1 Alapgondolata és az alkalmzás feltételei
2 Hipotézisek
3 A próbastatisztika
4 A próba végrehajtásának lépései
5 Példa
6 A próba matematikai háttere
7 Megjegyzések
8 Források

[szerkesztés] Alapgondolata és az alkalmzás feltételei

A próba alapgondolata, hogy a populációt m átlagú (várható értékű) és σ szórású normális eloszlásúnak feltételezzük és mintavételezéssel tesztelni kívánjuk, hogy az m szám tényleg tekinthető-e a populációs átlagnak, vagy ez a feltételezésünk nem tartható. A populációból véletlen módon egy n elemszámú mintát veszünk (x₁, x₂, ... ,x_n) a minta értékeiből átlagot számolunk ( $\mbox{ }_{\overline{x}}$ ) és meghatározzuk az átlag eltérését az m feltételezett populációs átlagtól. A kérdés, hogy az $\mbox{ }_{\overline{x}}$ – m különbség mértéke vajon

köszönhető-e a mintavétel véletlen hibájának, vagy
bizonyos p valószínűségű kockázatot vállalva (szignifikanciaszint) utal-e arra, hogy a populációs átlag nem lehet m.

A kérdést az adott p valószínűségű kockázat vállalása mellet szándékozunk megválaszolni. Ha a populáció normális eloszlásának görbéjén a minta átlaga olyan messze van a várható értéktől, hogy az olyan és annál távolabbi értékek valószínűsége a görbe szerint kisebb mint p, akkor nem véletlen eltérésre gyanakodunk, ha ennél nagyobb az előfordulási valószínűsége, akkor maradunk az eredeti feltételezésnél.

Eszerint az u-próba feltétele, hogy a vizsgált populáció isméreve (valószínűségi változója)

intervallum vagy arányskálán mért
normális eloszlású
ismert szórású
ismert populációs átlagú (illetve várható értékű)

legyen. A próba a populációs átlagot teszteli, így az utolsó feltételt pontosabb úgy fogalmazni, hogy feltételezéssel kell rendelkeznünk a populáció átlagára vonatkozóan.

[szerkesztés] Hipotézisek

Kétoldali ellenhipotézist fogalmazunk meg, ha pusztán azt szeretnénk ellenőrizni, hogy a populáció átlaga tényleg az m szám-e:

$H 0$ : a populáció átlaga = m	(nullhipotézis)
$H 1$ : a populáció átlaga ≠ m	(kétoldali ellenhipotézis)

A „populáció átlaga” kifejezés helyett a valószínűség-elmélet terminológiájában itt is az „X valószínűségi változó várható értéke” áll. Ekkor a vizsgálat tárgya, hogy E(X) egyenlő-e m-mel. Ekkor a próba később említendő u paraméterét a u_p/2 értékkel hasonlítjuk össze.

Ha van olyan gyanúnk, illetve azt szeretnénk igazolni, hogy a populációs átlag valójában kisebb mint m vagy valójában nagyobb mint m, akkor egyoldai ellenhipotézist fogalmazunk meg. (Ekkor természetesen a mintaátlag a relációnak megfelelően kisebb, vagy nagyobb, mint m, hiszen különben nem is értelmes a mintából egyoldali eltérésre gyanakodni.)

$H 0$ : a populáció átlaga = m	(nullhipotézis)
$H 1$ : a populáció átlaga < m	(baloldali ellenhipotézis)

Illetve a másik lehetőség, hogy $H 1$ : a populáció átlaga > m (jobboldali ellenhipotézis). Ekkor a próba később említendő u paraméterét az u_p értékkel hasonlítjuk össze.

[szerkesztés] A próbastatisztika

Az egymintás u-próba próbastatisztikája

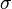$u = \frac {\bar x-m} {\sigma / \sqrt{n}}$

ahol

$\bar x$ a vizsgált valószínűségi változó átlaga a mintában,
$\sigma\,$ a vizsgált valószínűségi változó ismert szórása (ld. feltételek),
$m\,$ az előre adott érték, amihez az átlagot viszonyítjuk (ld. hipotézisek) és
$n\,$ a minta elemszáma.

[szerkesztés] A próba végrehajtásának lépései

lépés	megjegyzés
1. u kiszámítása a fenti képletből	ekkor lényegében a standardizálást végezzük el az $\mbox{ }_{s=\sigma/\sqrt{n}}$ sztenderd hibával
2. A p szignifikancia szint megválasztása	ez a legtöbb vizsgálat esetén 0,05; 0,01 vagy 0,005 (azaz 5%, 1% illetve 0,5%)
3. A p-hez vagy p/2-höz tartozó u értékek kikeresése	ezt a standard normáleloszlás táblázat alapján végezzük, a tipikus értékekre a lenti táblázatban feltüntettük őket
4. A döntést ezek után a választott p és választott típusú ellenhipotézis mellett a következők alapján hozzuk:

Megtartjuk $H 0$ -t, ha

	kétoldali ellenhipotézis	baloldali ellenhipotézis	jobboldali ellenhipotézis
p=0,05 (*)	-1,96 < u < 1,96	-1,64 < u	u < 1,64
p=0,01 (**)	-2,57 < u < 2,57	-2,32 < u	u < 2,32
p=0,005 (***)	-2,81 < u < 2,81	-2,57 < u	u < 2,57

Elvetjük $H 0$ -t ellenkező esetben.

Az eredményt a következőképpen interpretáljuk:

ha $H 0$ -t megtartottuk, akkor az egymintás u-próba nem mutat ki szignifikáns különbséget a vizsgált minta átlaga (valószínűségi változó mintabeli átlaga) és az adott m érték között (p szignifikancai szinten)
ha $H 0$ -t elvetettük, akkor elfogadjuk az ellenhipotézist illetve a mintában a vizsgált povalószínűségi változó átlaga szignifikánsan eltér az adott m értéktől (p szignifikancai szint mellett).

Megjegyzés. A döntésnél szereplő egyenlőtlenségben lévő határok kétoldali ellenhipotézisnél tetszőleges p szignifikancia szint esetén:(-|u_p/2| , |u_p/2| ), egyoldalinál (-|u_p| , +∞ ) illetve ( -∞, |u_p| ). Az u_p/2 (ill. u_p) érték kiválasztása a standard normális eloszlás táblázatából történik. Azt az x értéket kell kikeresni melynél nagyobb értéket standard normális eloszlású valószínűségi változó csak p/2 (illetve p) valószínűséggel vesz fel. Például p = 0,05 esetén p/2 = 0,025. Az ehhez közeli, de már nagyobb értéket megkeressük a táblázaton belül a &Phi(x); értékek között és leolvassuk azt az x értéket, amely ehhez a &Phi(x);-hez tartozik.

[szerkesztés] Példa

1. Arra vagyunk kíváncsiak, hogy egy pedagógiai program valóban gyorsítja-e az óvodás gyerekek értelmi képességeinek fejlődését. Azt értelmi képesség mérésére az intelligencia hányados, az un. IQ hivatott. Ez olyan mérőeszköz, ami intervallum skálán mér, tudjuk, hogy a populációban normális eloszlást követ és tudjuk, hogy a 100-as IQ mutatja az átlagos képességet. Egy teljesen átlagos óvodai csoportban tehát nem tér el lényegesen (szignifikánsan) az IQ átlagos értéke a 100-as értéktől. Az IQ mérésére használt tesztek szórását ismerjük, a legtöbb ilyen tesz 15-ös, 16-os vagy 24-es szórású. Mi most egy 16-os szórású teszttel fogunk mérni. Látható, hogy az egymintás u-próba alkalmazásának feltételei adottak.

A vizsgálatunkban összesen 71 óvodás korú gyermek vesz részt, akiken alkalmazták a vizsgált pedagógiai módszert. Egy év alkalmazás után a gyerekek IQ-ját az adott teszttel megmértük és azt kaptuk, hogy a 71 gyermek átlagos IQ-ja 105. Ez egy kicsit magasabb érték, mint az átlag, de nem tudjuk, hogy ez a különbség pusztán csak a véletlennek tulajdonítható (szinte soha nem kapunk pontosan 100-as átlagot egyetlen óvodai mintában sem), vagy tekinthető a 100-as értéktől való szisztematikus eltérésnek.

Ennek a kérdésnek az eldöntésére egymintás u-próbát alkalmazunk. A vizsgált valószínűségi változónk az IQ. Ez normális eloszlású a populációban, intervallumskálán mért és ismerjük a szórását (σ = 16). A mintánkban az átlag $\bar x$ = 105, A minta elemszáma n = 71, az előre megadott m érték az m = 100, hisz ez jelöli az átlagos teljesítményt s mi arra vagyunk kíváncsiak, hogy a mi csoportunk teljesítménye szignifikánsan eltér-e ettől. Ennek megfelelően az u próbastatisztikánk a jelen vizsgálat esetében

$u = \frac {\bar x-m} {\sigma / \sqrt{n}} = \frac {105-100} {16 / \sqrt{71}} \approx 2,633$

Ha p = 0,05-nek választjuk a szignifikancia szintet, akkor a táblázat beli érték u_p/2 = u_0,025 = 1,96, vagyis ha 5% kockázatot vállalunk arra nézve, hogy esetleg helytelenül vetjük el a nullhipotézist, akkor csak 1,96-nál nagyobb vagy -1,96-nál kisebb próbastatisztika értékek esetén tudjuk elvetni azt. Jelenlegi a helyzet próbastatisztika és a táblázatbeli érték viszonyában a következő.

u ≈ 2,633 miatt u > 2,632 > 1,96 = u_0,025

azaz |u| ≥ u_p/2 teljesül.

Így a nullhipotézist elvethetjük, az egymintás u-próba szerint szignifikáns különbség van (p = 0,05-ös szignifikancia szint mellett) a pedagógiai programban részt vett óvodások átlagos IQ-ja és a 100-as érték között.

2. Az Egyesült Államokban egy teljeskörű felmérés szerint az elsőéves egyetemisták hetente 7,5 órát töltenek bulizással. Az adatok szórása 7 óra. Egy egyetem rektora gyanakodik, hogy náluk a hallgatók nem buliznak ennyit, ezért 100 fős véletlen mintát vesz az egyetemének elsőévesei közül (kb. 3000 elsős van). A mintavétel eredménye 6,6 órás átlag. Kimutatható-e szignifikáns eltérés a populációs átlagtól?

Az a gondolatunk, hogy az országos felmérés átlagát tekintjük a 3000 fős egyetemi populáció átlagának és ezt ellenőrizzük u-próbával, tehát: $H 0$ : μ = 7,5, itt μ az egyetem elsőéveseinek populációs átlaga. A rektor gyanúja miatt érdemes azt az egyoldali ellenhipotézist venni, hogy μ < 7,5. Tehát

m = 7,5

$\mbox{ }_{\bar x}$ = 6,6

σ = 7

n = 100

Ekkor a képlet szerint u = -1,29. Így az u-próba nem járt sikerrel baloldali ellenhipotézisű, 5%-os szignifikanciaszinten sem, hiszen -1,64 < -1,29 és így azt mondhatjuk, hogy a 7,5 órás átlagtól való eltérés köszönhető a véletlennek is (ez nyilván az adatok nagy szórása miatt van így). Tehát nem mutatható ki szignifikáns különbség az országos átlagtól.

[szerkesztés] A próba matematikai háttere

Mivel a vizsgált X valószínűségi változótól megköveteltük, hogy normális eloszlást kövessen, így az X₁, X₂, ... X_n mintáról elmondható, hogy a belőle képzett

$\overline X= \frac{1}{n} \sum_{i=1}^{n} X_i$

valószínűségi változó is normális eloszlást követ. Mivel σ az X szórását jelöli, így az $\overline X$ szórása $\sigma /\sqrt n$ . Ha most meggondoljuk, hogy a – matematikailag precízebben megfogalmazott – nullhipotézis szerint m az X várható értékével azonos, akkor látható, hogy az

$u = \frac {\overline X-m} {\sigma / \sqrt{n}}$

próbastatisztika standard normális eloszlást fog követni. Emiatt bármilyen 1 > p > 0 esetén meg lehet határozni azt az u_p/2 értéket, melyre

$1-p = \bold P \left( -u_{p/2} < \frac {\overline X - m} {\sigma / \sqrt n} < u_{p/2}| H_0 \right) = \Phi (u_{p/2}) - \Phi (-u_{p/2}) = 2\Phi (u_{p/2})-1$

ahol Φ(x) a standard normális eloszlásfüggvény. Ez azt jelenti, hogy ha igaz a nullhipotézis, akkor az u próbastatisztika értéke 1-p valószínűséggel a (-u_p/2, u_p/2) intervallumba kell, hogy essen.

[szerkesztés] Megjegyzések

Az egymintás u-próba bizonyos tekintetben az egymintás t-próba párja. Az egymintás t-próba ugyanezt a nullhipotézis vizsgálja, csak nem feltétele az szórás értékének előzetes ismerete, hanem azt a minta adataiból becsli. A próbastatisztika képlete is nagyon hasonló, csak benne az ismert σ szórás helyett a mintából becsült s szórás szerepel. Természetesen a két próba matematikai háttere is nagyon hasonló.

A szakirodalom nem teljesen egységes annak tekintetében, hogy a nullhipotézis elvetéséről vagy megtartásáról szóló döntésben az |u| és $u p$ közötti két egyenlőtlenség közül melyiknél engedi meg az egyenlőséget. Ennek gyakorlati jelentősége nem igazán van, az alkalmazások során nagyon ritkán adódik, hogy a kiszámított próbastatisztika pontosan egybeesik a táblázatbeli értékkel. Ha esetleg mégis így alakul, akkor az eredmény úgy interpretálható, hogy a nullhipotézis elvetése esetén a kockázat pontosan megegyezik a szignifikancia szinttel, s innen a kutató (és a tudós társadalom) szája ízétől függ, hogy ebben inkább a nullhipotézis elvetésének, vagy inkább a nullhipotézis megtartásának zálogát látja.

Érdemes megfigyelni az óvatos fogalmazást a nullhipotézis megtartása esetén. Az általunk meghatározott p szignifikancia szint az elsőfajú hiba elkövetésének valószínűségét adja meg. Ha el tudom vetni a nullhipotézist, akkor ekkora kockázatot vállalok arra nézve, hogy esetleg hiba elvetni. Amennyiben viszont nem tudom elvetni a nullhipotézis, akkor elsőfajú hibát biztosan nem fogok elkövetni, ám elkövethetek másodfajú hibát, melynek kockázatáról semmit nem mond a próba. Ez indokolja, hogy ha a nullhipotézist megtartjuk, akkor nem azt mondjuk, hogy nincs szignifikáns különbség a minta átlaga és az előre megadott m érték között, hanem hogy az egymintás u-próba nem tudott szignifikáns különbséget kimutatni (ami ettől még lehet, hogy van). A másodfajú hiba elkövetésének valószínűségét az egymintás u-próba erőfüggvényének vizsgálatával tudjuk megállapítani.

Az egymintás u-próbára – az angol nyelvű szakirodalom alapján – szoktak z-próbaként, vagy egymintás z-próbaként is hivatkozni. Ez az elnevezés a magyar szakirodalomban ritkán fordul elő, ami azért is szerencsés, mert a magyar szakirodalom egy másik próbát is szokott néha z-próbának nevezni (ami korrelációs együtthatók közötti szignifikáns különbségek kimutatására alkalmas).

[szerkesztés] Források

Fazekas I. (szerk.) (2000): Bevezetés a matematikai statisztikába. Kossuth Egyetemi Kiadó, Debrecen.
Lukács O. (2002): Matematikai statisztika. Műszaki Könyvkiadó, Budapest.
Michaletzky Gy. – Mogyoródi J. (1995): Matematikai statisztika, Nemzeti Tankönyvkiadó, Budapest.
Michelberger P. – Szeidl L. – Várlaki P. (2001): Alkalmazott folyamatstatisztika és idősor-analízis. Typotex Kiadó, Budapest.
Petres T. – Tóth L. (2001): Statisztika. JATEPress, Szeged.
Vargha A. (2000): Matemtatikai statisztika pszchológiai, nyelvészeti és biológiai alkalmazásokkal. Pólya Kiadó, Budapest.