Kétmintás u-próba

A Wikipédiából, a szabad lexikonból.

A kétmintás u-próba a statisztikai hipotézisvizsgálatok közül a paraméteres próbák közé tartozik. A próba azt vizsgálja, hogy két külön mintában egy-egy valószínűségi változó átlagai egymástól szignifikánsan különböznek-e.

Tartalomjegyzék

1 A próba alkalmazásának feltételei
2 A próba nullhipotézise
3 A próbastatisztika
4 A próba végrehajtásának lépései
5 Példa
6 A próba matematikai háttere
7 Megjegyzések
8 Források

[szerkesztés] A próba alkalmazásának feltételei

a vizsgált valószínűségi változók normális eloszlásúak
a vizsgált valószínűségi változók intervallum vagy arányskálán mértek
a vizsgált valószínűségi változók populáción belüli szórásai ismertek (tehát nem a minta alapján kell becsülnünk őket)
a vizsgált valószínűségi változók függetlenek

[szerkesztés] A próba nullhipotézise

Nullhipotézis: a két mintában a két átlag statisztikai szempontból megegyezik.

Alternatív hipotézis: a két mintában a két átlag statisztikai szempontból nem egyezik meg.

A "statisztikai szempontból" kifejezés itt arra utal, hogy az eltérés a két átlag között olyan minimális, hogy pusztán csak a véletlen ingadozásnak tulajdonítható (ekkor a két átlag statisztikai szempontból azonosnak tekinthető), vagy jelentősen nagyobb, mint ami a véletlennel magyarázható (ekkor a két átlag statisztikai szempontból nem tekinthető azonosnak).

Valójában a fenti két hipotézis precíz matematikai megfogalmazása a következő.

H₀: Az X és Y valószínűségi változók várható értékei megegyeznek, (E(X) = E(Y)).
H₁: Az X és Y valószínűségi változók várható értékei nem egyeznek meg, (E(X) ≠ E(Y)).

[szerkesztés] A próbastatisztika

A kétmintás u-próba próbastatisztikája

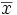$u = \frac {\overline x- \overline y} {\sqrt { \frac{\sigma_x^2}{n} + \frac{\sigma_y^2}{m} } }$

ahol

$\overline x$ az egyik valószínűségi változó átlaga a mintájában,
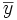$\overline y$ a másik valószínűségi változó átlaga a mintájában,
$σ x$ az egyik valószínűségi változó ismert szórása (ld. feltételek),
$σ y$ a másik valószínűségi változó ismert szórása (ld. feltételek),
n az egyik minta elemszáma és
m a másik minta elemszáma.

[szerkesztés] A próba végrehajtásának lépései

Az u próbastatisztika értékének kiszámítása.
A p szignifikancia szint megválasztása. (Ez a legtöbb vizsgálat esetén 0,05 vagy 0,01.)
A p szignifikancia szinttől függő u_p/2 érték kiválasztása a próbának megfelelő táblázatból. A táblázat jelen esetben a standard normális eloszlás táblázata, ahol azt az x értéket kell kikeresni melynél nagyobb értéket standard normális eloszlású valószínűségi változó csak p/2 valószínűséggel vesz fel. (Ez az érték p=0,05 esetén u_p/2 = u_0,025 = 1,96, p=0,01 esetén u_p/2 = u_0,05 = 2,576.
A nullhipotézisre vonatkozó döntés meghozása.
- Ha |u| ≥ u_p/2, akkor a nullhipotézist elvetjük, az alternatív hipotézist tartjuk meg, és az eredményt úgy interpretáljuk, hogy a két mintában a valószínűségi változók átlagai szignifikánsan eltérnek egymástól (p szignifikancai szint mellett).
- Ha |u| < u_p/2, akkor a nullhipotézist megtartjuk, amit úgy interpretálunk, hogy a kétmintás u-próba nem mutat ki szignifikáns különbséget a két mintában a valószínűségi változók átlagai között (p szignifikancai szint mellett).

[szerkesztés] Példa

[szerkesztés] A próba matematikai háttere

Az egymintás u-próbához hasonlóan a kétmintás esetben is azt lehet megmutatni, hogy az u próbastatisztika standard nomális eloszlást követ. Részletesebben azt, hogy ha X jelöli az egyik, Y a másik valószínűségi változót, X₁, X₂, ... , X_n, az egyik mintát Y₁, Y₂, ... , Y_m a másik mintát, valamint σ_x és σ_y rendre az X és az Y szórását, akkor az

$\overline X= \frac{1}{n} \sum_{i=1}^{n} X_i$

és

$\overline Y= \frac{1}{m} \sum_{j=1}^{n} Y_j$

jelöléseket bevezetve az

$u = \frac {\overline X- \overline Y} {\sqrt { \frac{\sigma_x^2}{n} + \frac{\sigma_y^2}{m} } }$

próbastatisztika standard normális eloszlást fog követni. Emiatt bármilyen 1 > p > 0 esetén meg lehet határozni azt az u_p/2 értéket, melyre

$1-p = \bold P \left( -u_{p/2} < \frac {\overline X- \overline Y} {\sqrt { \frac{\sigma_x^2}{n} + \frac{\sigma_y^2}{m} } } < u_{p/2} \mid \ H_0 \right) = \Phi (u_{p/2}) - \Phi (-u_{p/2}) = 2\Phi (u_{p/2})-1$

ahol Φ(x) a standard normális eloszlásfüggvény. Ez azt jelenti, hogy ha igaz a nullhipotézis, akkor az u próbastatisztika értéke 1-p valószínűséggel a (-u_p/2, u_p/2) intervallumba esik.

[szerkesztés] Megjegyzések

A kétmintás u-próba bizonyos tekintetben az kétmintás t-próba párja. A kétmintás t-próba ugyanezt a nullhipotézist vizsgálja, csak nem feltétele az szórások értékének előzetes ismerete, hanem azokat a minták adatai alapján becsli. A próbastatisztika képlete is nagyon hasonló, csak benne az ismert σ_x és σ_y szórások helyett a mintából becsült s_x és s_y szórások szerepelnek. Természetesen a két próba matematikai háttere is nagyon hasonló.

A szakirodalom nem teljesen egységes annak tekintetében, hogy a nullhipotézis elvetéséről vagy megtartásáról szóló döntésben az |u| és $u p$ közötti két egyenlőtlenség közül melyiknél engedi meg az egyenlőséget. Ennek gyakorlati jelentősége nem igazán van, az alkalmazások során nagyon ritkán adódik, hogy a kiszámított próbastatisztika pontosan egybeesen a táblázatbeli értékkel. Ha esetleg mégis így alakul, akkor az eredmény úgy interpretálható, hogy a nullhipotézis elvetése esetén a kockázat pontosan megegyezik a szignifikancia szinttel, s innen a kutató (és a tudós társadalom) szája ízétől függ, hogy ebben inkább a nullhipotézis elvetésének, vagy inkább a nullhipotézis megtartásának zálogát látja.

Érdemes megfigyelni az óvatos fogalmazást a nullhipotézis megtartása esetén. Az általunk meghatározott p szignifikancia szint az elsőfajú hiba elkövetésének valószínűségét adja meg. Ha el tudom vetni a nullhipotézist, ekkora kockázatot vállalok arra nézve, hogy esetleg hiba elvetni. Amennyiben viszont nem tudom elvetni a nullhipotézis, akkor elsőfajú hibát biztosan nem fogok elkövetni, ám elkövethetek másodfajú hibát, melynek kockázatáról semmit nem mond a próba. Ez indokolja, hogy ha a nullhipotézist megtartjuk, akkor nem azt mondjuk, hogy nincs szignifikáns különbség a minta átlaga és az előre megadott m érték között, hanem hogy az egymintás u-próba nem tudott szignifikáns különbséget kimutatni (ami ettől még lehet, hogy van).

[szerkesztés] Források

Fazekas I. (szerk.) (2000): Bevezetés a matematikai statisztikába. Kossuth Egyetemi Kiadó, Debrecen.
Lukács O. (2002): Matematikai statisztika. Műszaki Könyvkiadó, Budapest.
Michaletzky Gy. – Mogyoródi J. (1995): Matematikai statisztika, Nemzeti Tankönyvkiadó, Budapest.
Michelberger P. – Szeidl L. – Várlaki P. (2001): Alkalmazott folyamatstatisztika és idősor-analízis. Typotex Kiadó, Budapest.
Vargha A. (2000): Matematikai statisztika pszchológiai, nyelvészeti és biológiai alkalmazásokkal. Pólya Kiadó, Budapest.