November 18.

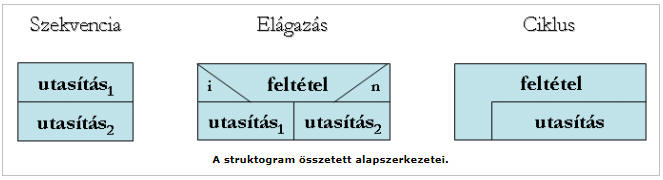
Algoritmus leíró eszközök

(forrás: http://progalap.elte.hu/downloads/seged/eTananyag/lecke4_lap1.html#hiv3)

Feladatok

Programozási tételek: https://kahoot.it/

Euklideszi algoritmus: Két természetes szám legnagyobb közös osztója határozható meg a következőképpen:

Alapötlete az, hogy a legnagyobb közös osztó nem változik, ha a nagyobb számot a két szám különbségével helyettesítjük. Például 252 és 105 legnagyobb közös osztója 21, amely legnagyobb közös osztója a 105 és a 147 = 252 − 105 számoknak is. Ez a helyettesítés csökkenti a nagyobb számot, így a cserék ismétlésével egyre kisebb számokat kapunk, egészen addig, amíg a két szám egyenlővé nem válik. Ez az eddigi számpárok, így az eredeti számpár legnagyobb közös osztója. Az algoritmus lépésein visszafelé menve találunk két egész (akár negatív) tényezőt, amelyek felhasználásával a legnagyobb közös osztó kifejezhető a két kiindulási szám lineáris kombinációjaként.

Ha feltesszük, hogy a kivonások és a maradékos osztások ideje körülbelül megegyezik, akkor az algoritmusnak van egy gyorsabb változata is, amely a kivonások helyett maradékos osztással működik. Ennek lényege, hogy ha a nagyobb szám sokkal nagyobb, mint a kisebb, akkor sok kivonást kell elvégezni addig, amíg a két szám szerepe felcserélődik. A maradékképzés művelete ezt a sok kivonást egy lépésben végzi el. Az algoritmus akkor ér véget, amikor a maradék nulla lesz. Ekkor a legnagyobb közös osztó éppen a kisebb szám.

    A feladat megoldása: euklidesz.cs

Eratoszthenész szitája: Egy adott számig prímek keresése osztás nélkül.

(forrás: Fekete Ildikó: Dan Brown Digitális erodje és a nyilvános ˝ kulcsú titkosítás (https://web.cs.elte.hu/blobs/diplomamunkak/bsc_matelem/2015/fekete_ildiko.pdf))

1. Írjuk fel a számokat egymás alá 2-től ameddig a prímtesztet elvégezni kívánjuk.

2. Kezdjünk egy B listát 2-vel, az első prím számmal.

3. Húzzuk le 2-t és az összes többszörösét az A listáról.

4. Az első át nem húzott szám az A listán a következő prím. Írjuk fel a B listára.

5. Húzzuk át az így megtalált következő prímet és az összes többszörösét.

6. Ismételjük a 3–5. lépéseket, amíg az A listán nincs minden szám áthúzva.

A feladat megoldása: eratoszthenész.cs

 

 

 

Házi feladat: Keressük meg az első olyan faktoriális számot, amely két 0-ra végződik.