A quicksort az oszd-meg-és-uralkodj elvén alapuló rendezés, azaz a feladatot több kisebb részfeladatra bontja, amelyek hasonlóak az eredetihez és rekurzív módon oldják meg a részfeladatokat, amelyeket összevonva adódik a feladat megoldása. Minden algoritmus, amely ezen az elven alapul 3 lépésből áll. Felosztja a feladatot több kisebb részfeladatra, "uralkodik" a részfeladatokon való megoldásukkal és összevonja a részfeladatokat, hogy megkapja az eredeti feladat megoldását.

A quicksort egy helyben rendező algoritmus, azaz a rendezés a tömbön belül történik, legfeljebb csak állandó számú elem tárolódik a tömbön kívül.

Továbbá nem stabil rendezés, azaz az azonos kulcsú elemek egymáshoz viszonyított sorrendjét nem feltétlenül őrzi meg. Például, ha van kettő 32-es, akkor nem biztos, hogy ugyanabban a sorrendben lesznek a rendezés végén, mint rendezés előtt voltak.

Az összehasonlító rendezések közé tartozik, azaz az elemek sorrendjét azok összehasonlításával állapítja meg.

Működése:

Az algoritmus kulcsa a felosztás, amely mindig kiválaszt véletlenszerűen egy $x$ pivot (tengely vagy őrszem) elemet. Ez lehet a tömb első eleme, utolsó eleme, középső eleme, vagy egy random elem. Azért érdemes random elemet választani pivot elemnek, mert ezzel a „balszerencsés” bemenetek valószínűségét csökkenteni tudjuk. Ezután ezt az elemet kimentjük egy $x$ változóba és a legutolsó elemet az $x$ helyére rakjuk. A felosztás során 4 részre bonjuk a tömböt: $x$-nél kisebbek vagy egyenlőek, $x$-nél nagyobbak, a még meg nem vizsgált elemek és maga a pivot elem.

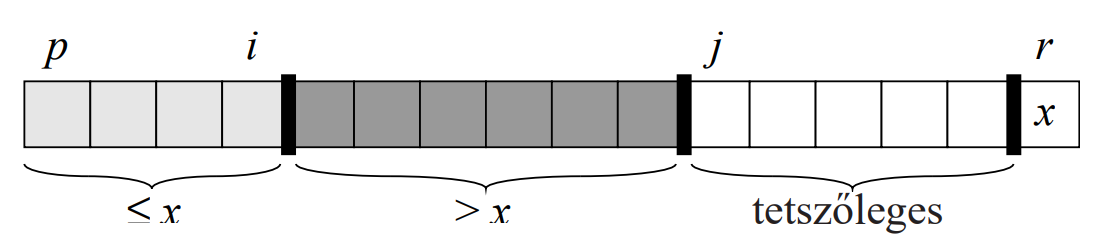
Egy rekurzív folyamat végén a tömb elemei 3 részben lesznek: $x$-nél nagyobbak, $x$-nél kisebbek vagy egyenlőek és maga a pivot elem, amelyet behelyezünk a nagyobbak és a kisebbek vagy egyenlőek közé, oly módon, hogy a legbaloldalibb $x$-nél nagyobb elemet a tömb végére helyezzük és a helyére berakjuk a pivotot.

Két fő részből áll: a rekurzív rendezés és a particionálás.

Particionálás:

1. Kiválasztunk egy pivot elemet és kirakjuk egy $x$ nevű változóba.
2. A pivot elem helyére rakjuk a tömb legutolsó elemét.
3. A tömb elejétől elindulunk $i$-vel és addig megyünk, amíg nem találunk a pivot elemnél nagyobb elemet. Ha találtunk ilyet megállunk.
4. Elindítjuk $j$-t, ami $j = i + 1$-től indul. Addig megyünk $j$-vel, amíg nem találunk a pivot elemnél kisebbet.
5. Ekkor az $i$-nél egy a pivotnál nagyobb elem van, $j$-nél a pivotnál egy kisebb elem van, tehát meg kell cserélni őket.
6. A csere után megnöveljük $i$-t eggyel és a $j$-vel folytatjuk tovább a tömb bejárását.
7. Ha $j=r$, azaz végig értünk, $i$-edik helyen lévő elemet (a nagyobbak legbaloldalibb elemét) a tömb végére helyezzük. Helyére bekerül a pivot elem, ami pont a nagyobbak és a kisebb egyenlőek közé fog kerülni.
8. Majd visszatér $i$-vel, innen fogjuk tudni, hogy meddig tart a kisebb egyenlőek résztömbje és honnan indul a nagyobbak résztömbje. A particionálást ezekre a résztömbökre is lefuttatjuk rekurzívan.

Műveletigény:

A gyorsrendezés viselkedése nem a bemenő elemektől, hanem azok egymáshoz viszonyított helyétől függ. A legrosszabb felosztás, ha a felosztó algoritmus az eredeti tömböt egy $n-1$ és egy $0$ elemű tömbre osztja fel. A legjobb felosztás, ha a felosztó algoritmus az eredeti tömböt két $\frac{n}{2}$ elemű tömbnél nem nagyobb tömböt hoz létre. A gyorsrendezés átlagos futási ideje sokkal közelebb áll a legjobb futási időhöz.

• $MT(n) \in \Theta(n^2)$, ez ritkán fordul elő, mivel véletlen a pivot elem választása.
• $AT(n) \in O(n \cdot log \space n)$
• $mT(n) \in \Theta(n \cdot log \space n)$

Gyakorlati alkalmazása:

A vegyes rendezésben szokták használni, ahol összekombinálják a beszúró rendezést egy gyors rendezéssel (merge sort, quicksort, heap sort). Ha kevés elemet kell rendezni, akkor a beszúró rendezés fut le, ha sok elemet kell rendezni, akkor a gyors rendezést használja a vegyes rendezés.

A C++ beépített rendező algoritmusa (std::sort) egy introsort-nak nevezett rendezést használ, amely quicksortttal indul és átvált heapsortra, ha a rekurzió mélysége elér egy bizonyos szintet.