Radix rendezés (Radix sort)

Összehasonlításon alapuló rendezések:

Az eddigi rendezések összehasonlító rendezések voltak. Bármely összehasonlító algoritmusnak a legrosszabb esetben $\Omega (n \cdot log \space n)$ összehasonlításra van szüksége $n$ elem rendezéséhez.

Döntési fa modell:

Az összehasonlító rendezéseket döntési fákkal modellezzük. A döntési fa egy adott elemű bemenet rendezése során történt összehasonlításokat ábrázoló bináris fa.

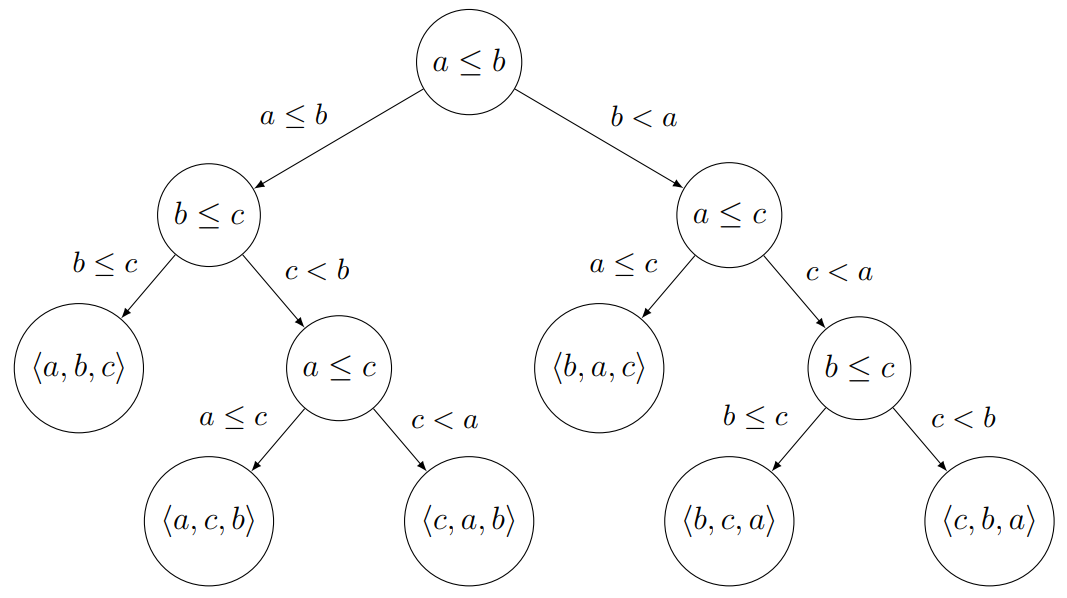
A rendezendő számokat kulcsoknak is szokás nevezni. A döntési fa belső csúcsaiban vannak a kulcs összehasonlítások, leveleiben a rendezés eredményeként adódó lehetséges sorozatok. Az $n$ elemű bemenetnek mind az $n!$ permutációja meg kell jelenjen egy-egy levélen, azaz a döntési fának legalább $n!$ levele van.

A fa gyökerét és legtávolabbi levelét összekötő út hossza adja meg azoknak az összehasonlításoknak a számát, melyeket a rendezőalgoritmus a legrosszabb esetben végez.

Lineáris idejű rendezések:

Ezek a rendezések nem kulcsösszehasonlításokkal rendeznek, hanem osztályozzák a kulcsokat. Egyes rendezések, viszont használnak kulcsösszehasonlító segédrendezéseket.

Radix rendezés:

A kulcsok $r$ alapú számrendszerben felírt, $d$ számjegyű, előjel nélküli egész számok. Ez lesz a $dDigitNumber$ típus. Ha kell vezető nullákat írunk a számok elé, hogy $d$ számjegyű legyen.

A kulcsok számjegyeit a legkevésbé fontos (jobb szélső) számjegytől a legfontosabb (bal szélső) számjegyig minden helyiérték szerint rendezzük egymás után egy stabil rendezéssel. Azért fontos, hogy stabil rendezés legyen, mert az $i$-edik számjegy szerinti rendezésnél, azonos számjegyek esetén meg kell őrizni a rendezettséget. A hatékonyság miatt fontos, hogy lineáris időben rendezzenek.

A szétválogató rendezés (distributing sort) láncolt listák számjegy szerinti rendezésére, míg a leszámláló rendezés (counting sort) tömbök rendezésére alkalmas.

Műveletigény:

Ez $\Theta (d \cdot rendezés(n))$ költségű, ahol a $rendezés(n)$ a belső rendezésünk költsége.

Gyakorlati alkalmazása:

Néha használják a radix rendezést összetett kulcsú rekordok rendezésére. Ilyen összetett kulcs például a dátum, ami három komponenst (év, hó, nap) tartalmaz.