Szükséges előismeret: Függvények aszimptotikus viselkedése, Jelölések
Algoritmusok és adatszerkezetek 1. > Láncolt listák > Egyirányú láncolt listák
Egyirányú láncolt listák (Singly linked lists)
A láncolt lista olyan adatszerkezet, amelyben az objektumok lineáris sorrendben követik egymást. A tömböknél a lineáris sorrendet a tömbindexek határozzák meg, ezzel szemben a láncolt listákban pointerek valósítják meg az elemek lineáris elrendezettségét. A lista minden objektuma tartalmaz egy mutatót, amely a következő objektumra mutat.
Egy lista lehet egyszeresen vagy kétszeresen láncolt, lehet rendezett vagy rendezetlen, és lehet ciklikus vagy nem ciklikus.
Ha egy lista rendezett, akkor a legkisebb kulcsérték a lista fejében található, a legnagyobb kulcsérték pedig a lista végében. Ha egy lista rendezetlen, akkor elemeinek sorrendje tetszőleges lehet. A ciklikus listát az jellemzi, hogy a fej előző pointere a lista végére, a lista utolsó elemének következő pointere a fej elemre mutat.
Tömbbel való összehasonlítás:
Láncolt lista előnyei:
- gyors beszúrás és törlés
- a rendezett beszúrás/törlés nem igényel elemmozgatást. Persze a beszúrás/törlés helyének megtalálása rendezett esetben $O (n)$.
- dinamikus a mérete
Láncolt lista hátrányai:
- nem indexelhető konstans műveletigénnyel, csak $O (n)$-nel.
- minden listaelem több memóriát igényel, mivel tárolni kell a következő elemre mutató pointert is.
Egyirányú láncolt listák:
Listaelem típusa:
A bejáráshoz pointereket használunk. Egy elem adattagjainak elérése: $p \rightarrow key$, $p \rightarrow next$ (helyes még $(^*p).key$, $(^*p).next)$. Ha új listaelemet szeretnénk létrehozni: $p = \text{new} \space E1$, feleslegessé vált listaelem felszabadítása: $delete \space p$.
| $E1$ |
| $+ \space key : \mathcal{T}$ $+ \space next : E1^*$ $+ \space ...$ |
| $+ \space E1() \space \{ next := \emptyset \}$ |
Egyirányú láncolt listák fajtái:
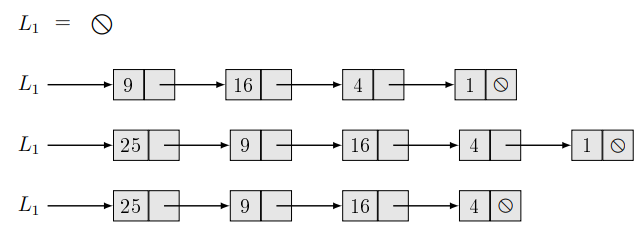
Egyszerű, egyirányú láncolt lista (S1L (Simple 1-way List)):
Az első elemre egy pointer mutat. Ha még nincs eleme a listának, ez a pointer nullpointer.

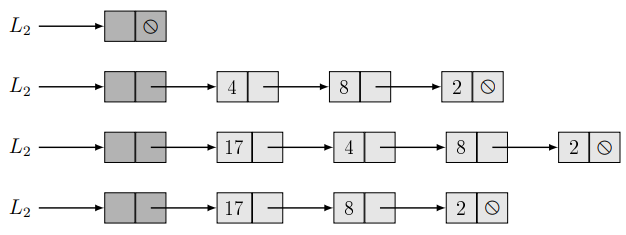
Fejelemes egyirányú láncolt lista (H1L (Header node + 1-way List)):
Hasonló az S1L-hez, de a H1L mindig tartalmaz egy fejelemet (őrszem vagy sentinel elemet) a lista elején. Ez az elem ugyanolyan felépítésű, mint a lista összes többi eleme, de nem tárol valódi adatot. Célja, hogy a lista elején végzett műveleteket megkönnyítse, mert így a lista elejére mutató pointerünk soha nem nullpointer. Továbbá segítségével egyszerűbben a lista határait ellenőrizni.
Műveletek egyirányú láncolt listákkal:
(Feltételezzük, hogy a lista növekvően rendezett!)
Keresés kulcs alapján:
Lineáris módon keresi a megfelelő kulcsú elemet a listában, és az arra mutató pointert adja vissza, ha megtalálta az elemet. Ha nem találta meg az elemet a listában, akkor a visszaadott érték nullpointer, így nem kell a logikai változó, amit a lineáris keresés tételénél tanultunk.
| $findInS1L(L : E1^*, dataToFind : \mathcal{T}) : E1^*$ |
| $p := L$ | ||||
| $p \neq 0 \land p \rightarrow key < dataToFind$ | ||||
| $p := p \rightarrow next$ | ||||
|
$p \neq 0 \land p \rightarrow key = dataToFind$
|
||||
| $\text{return} \space p$ | $\text{return} \space \emptyset$ | |||
| $findInH1L(L : E1^*, dataToFind : \mathcal{T}) : E1^*$ |
| $p := L \rightarrow next$ | ||||
| $p \neq 0 \land p \rightarrow key < dataToFind$ | ||||
| $p := p \rightarrow next$ | ||||
|
$p \neq 0 \land p \rightarrow key = dataToFind$
|
||||
| $\text{return} \space p$ | $\text{return} \space \emptyset$ | |||
Ha H1L-el csináljuk csak az indulás különbözik, $p:= L \rightarrow next$ az induló lépés.
Beszúrás:
(Ha rendezetlen listába szeretnénk egy megadott elemet beszúrni, akkor egyszerűen csak a lista elejére szúrnánk be. Ekkor a műveletigénye $O (1)$ lenne.)
Beszúrás esetei:
- a lista belsejébe szúrunk be az új elemet
- a lista utolsó eleme után fűzzük be az új elemet
- a lista elejére szúrjuk be az új elemet
- üres listába fűzzük be az új elemet
Két elem címe kell: $p$ az aktuálisan vizsgált elem, ami elé fogunk befűzni, valamint $pe$ az előtte lévő elem címe. Megoldható egy pointerrel is, de kevesebb hibával jár, ha két pointert használunk. A négy eset között az a különbség, hogy az az elem, amelyik az aktuális elem előtt van, az nem mindig létezik, így egyedül ezt kell majd egy elágazással kezelni.
| $insertIntoS1L(\&L : E1^*, dataToInsert : \mathcal{T})$ |
| $pe := 0$ | ||||
| $p := L$ | ||||
| $p \neq 0 \land p \rightarrow key < dataToInsert$ | ||||
| $pe := p$ | ||||
| $p := p \rightarrow next$ | ||||
|
$p \neq 0 \land p \rightarrow key = dataToInsert$
|
||||
| $\text{SKIP}$ | $q := \text{new} \space E1$ | |||
| $q \rightarrow key := dataToInsert$ | ||||
| $q \rightarrow next := p$ | ||||
|
$pe = 0$
|
||||
| $L := q$ | $pe \rightarrow next := q$ | |||
| $insertIntoH1L(L : E1^*, dataToInsert : \mathcal{T})$ |
| $pe := L$ | ||||
| $p := L \rightarrow next$ | ||||
| $p \neq 0 \land p \rightarrow key < dataToInsert$ | ||||
| $pe := p$ | ||||
| $p := p \rightarrow next$ | ||||
|
$p \neq 0 \land p \rightarrow key = dataToInsert$
|
||||
| $\text{SKIP}$ | $q := \text{new} \space E1$ | |||
| $q \rightarrow key := dataToInsert$ | ||||
| $q \rightarrow next := p$ | ||||
| $pe \rightarrow next := q$ | ||||
Mivel a műveletnél $L$ pointer módosulhat, így fontos, hogy az cím szerint átvett paraméter legyen! Ha H1L-el csináljuk indulásnál $pe$ a fejelemre mutathat, hiszen az első elem előtt ott van mindig a fejelem, $p$ pedig a lista első elemére mutat. Mivel $pe$ nem lehet nullpointer, nincs szükség az elágazásra a befűzésnél. Továbbá a lista nem cím szerint adódik át, hiszen a fejelem nem változtatja meg a címét, így az arra mutató pointer biztosan nem fog változni.
Törlés:
Törlés esetei:
- a lista üres
- a törlendő elem a lista első eleme
- a törlendő elem a lista belsejében van
- a törlendő elem a lista utolsó eleme
Két elem címe kell: $p$ az aktuálisan vizsgált elem, ami elé fogunk befűzni, valamint $pe$ az előtte lévő elem címe. Ha az adott kulcsú elem nem található, akkor nem történik semmi.
| $deleteFromS1L(\&L : E1^*; dataToDelete : \mathcal{T})$ |
| $pe := 0$ | ||||
| $p := L$ | ||||
| $p \neq 0 \land p \rightarrow key < dataToDelete$ | ||||
| $pe := p; \space p := p \rightarrow next$ | ||||
|
$p \neq 0 \land p \rightarrow key = dataToDelete$
|
||||
|
$pe = 0$
|
$\text{SKIP}$ | |||
| $L := p \rightarrow next$ | $pe \rightarrow next := p \rightarrow next$ | |||
| $delete \space p$ | ||||
| $deleteFromH1L(L : E1^*; dataToDelete : \mathcal{T})$ |
| $pe := L$ | ||||
| $p := L \rightarrow next$ | ||||
| $p \neq 0 \land p \rightarrow key < dataToDelete$ | ||||
| $pe := p; \space p := p \rightarrow next$ | ||||
|
$p \neq 0 \land p \rightarrow key = dataToDelete$
|
||||
| $pe \rightarrow next := p \rightarrow next$ | $\text{SKIP}$ | |||
| $delete \space p$ | ||||
Mivel a műveletnél $L$ pointer módosulhat, így fontos, hogy az cím szerint átvett paraméter legyen! Ha H1L-el csináljuk az indulás hasonló, itt sem kell elágazás a kifűzésnél, mert $pe$ nem lehet nullpointer.
Ciklikus egyirányú listák:
Ciklikus esetben az utolsó listaelem $next$ mezője nem a nullpointer, hanem visszamutat a lista elejére.
Animáció
Az animáció fejlesztés alatt áll 😭😭
Struktogram
Animáció
Az animáció fejlesztés alatt áll 😭😭
Struktogram
Feladatok
Az alábbi feladatok a gyakorlatokon elvégzendő kötelező, illetve gyakorló feladatok.