Bináris keresőfa (Binary search tree)

Feladatok

Bináris keresőfák műveletei:

Műveletigény:

search:

insert:

min:

remMin:

del:

Bináris keresőfa rákövetkező művelete:

Egy bináris fát keresőfának nevezünk, ha minden belső csúcsára igaz, hogy a csúcs bal részfájában minden csúcs kulcsa kisebb, a jobb részfájában minden csúcs kulcsa nagyobb és minden kulcs egyedi a fában.

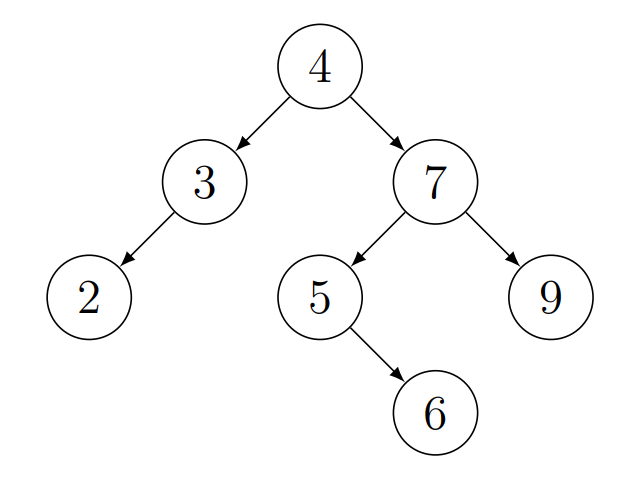
Egy bináris fát rendezőfának nevezünk, ha minden belső csúcsára igaz, hogy a csúcs bal részfájában minden csúcs kulcsa kisebb vagy egyenlő, a jobb részfájában minden csúcs kulcsa nagyobb vagy egyenlő és lehetnek duplikált kulcsok a fában.

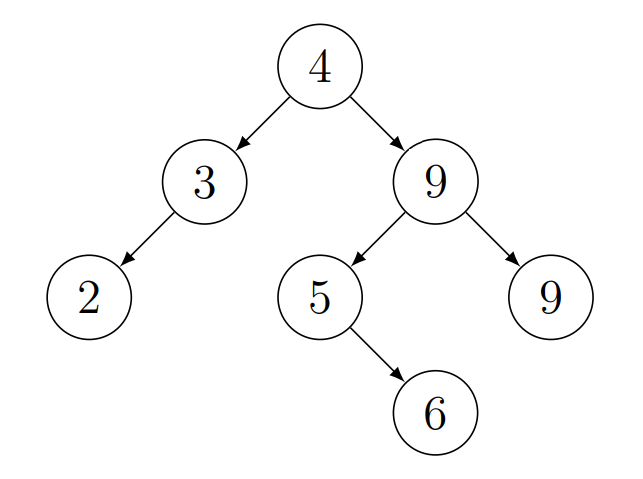
A bináris keresőfát inorder bejárással kiíratjuk egy szigorúan monoton növekvő sorozatot kapunk.

A leggyakoribb művelete a fában a tárolt kulcsok keresése. Az algoritmus a gyökérnél kezdi a keresést, és egy lefelé haladó utat jár be a fában. Minden érintett csúcsnál összehasonlítja a paraméterként kapott kulcsot a csúcs kulcsával. Ha a két kulcs egyenlő, a keresés befejeződik. Ha a paraméterként kapott kulcs kisebb, mint a csúcs kulcsa, akkor a csúcs bal oldali részfájában folytatódik a keresés, ha pedig nagyobb, akkor a jobb oldali részfájában. Ha nullpointerhez értünk a keresés sikertelen.

$search(t : Node^*; k : \mathcal{T}) : Node^*$

	$t \neq \emptyset \land t \rightarrow key \neq k$
	$k < t \rightarrow key$
	$t := t \rightarrow left$	$t := t \rightarrow right$
$\text{return} \space t$

Megváltoztatja a bináris keresőfával ábrázolt dinamikus halmazt. A módosítást természetesen úgy kell végrehajtani, hogy a bináris keresőfa tulajdonság megmaradjon.

A gyökértől indulunk és megyünk lefelé a kulcsösszehasonlításokkal mindaddig, amíg nullpointert nem találunk. Pontosan ennek a nullpointernek a helyére kell beilleszteni a kulcsot. Viszont, ha a kulcsösszehasonlítások során a kulcsok egyenlőek, akkor az azt jelenti, hogy a kulcs már benne van a fában. Mivel a keresőfában minden kulcs egyedi, így nem kell beszúrni ezt a kulcsot.

$insert(\&t : Node^*; k : \mathcal{T})$

$t = \emptyset$
$t := \text{new} \space Node(k)$	$k < t \rightarrow key$	$k > t \rightarrow key$	$k = t \rightarrow key$
	$insert(t \rightarrow left, k)$	$insert(t \rightarrow right, k)$	$\text{SKIP}$

A minimális kulcsú elem mindig könnyen megtalálható, ha addig követjük a bal oldali pointereket, amíg nullpointert nem találunk.

$min(t : Node^*) : Node^*$

	$t \rightarrow left \neq \emptyset$
	$t := t \rightarrow left$
$\text{return} \space t$

Először megkeressük a minimális kulcsú elemet. Mivel a minimális kulcsú elemnek nincs bal gyereke, így egyszerűen csak a jobb gyerekét rakjuk a helyére.

$remMin(\&t, \&minp : Node^*)$

$t \rightarrow left = \emptyset$
$minp := t$		$remMin(t \rightarrow left, minp)$
$t := minp \rightarrow right$
$minp \rightarrow right := \emptyset$

Megváltoztatja a bináris keresőfával ábrázolt dinamikus halmazt. A módosítást természetesen úgy kell végrehajtani, hogy a bináris keresőfa tulajdonság megmaradjon.

A $del()$ megkeresi a fában a törölni kívánt csúcsot, majd meghívja a $delRoot()$-ot.

A $delRoot()$ három esetet vizsgál meg. Ha $t$-nek nincs bal gyereke, akkor egyszerűen a jobb gyerekét kell a helyére rakni. Ha $t$-nek nincs jobb gyereke, akkor egyszerűen a bal gyerekét kell a helyére rakni. Végül, ha a csúcsnak két gyereke van, akkor $t$-nek azt a legközelebbi rákövetkezőjét kell a helyére rakni, melynek már nincs bal oldali gyereke. Ez a jobb oldali részfájának a legkisebb eleme lesz.

$del(\&t : Node^*, k : \mathcal{T})$

$t \neq \emptyset$
$k < t \rightarrow key$	$k > t \rightarrow key$	$k = t \rightarrow key$	$\text{SKIP}$
$del(t \rightarrow left, k)$	$del(t \rightarrow right, k)$	$delRoot(t)$

$delRoot(\&t : Node^*)$

$p := t$
$t \rightarrow left = \emptyset$	$t \rightarrow right = \emptyset$	$t \rightarrow left \neq \emptyset \land t \rightarrow right \neq \emptyset$
$t := p \rightarrow right$	$t := p \rightarrow left$	$remMin(t \rightarrow right, q)$
		$q \rightarrow left := p \rightarrow left$
		$q \rightarrow right := p \rightarrow right$
		$t := q$
$\text{delete} \space p$

Az aktuális elem inorder bejárás szerinti rákövetkezőjét keressük. Egy elem rákövetkezője a jobb oldali részfájának a legkisebb eleme vagy ha nincs jobb oldali részfája, akkor az az őse, amelytől balra helyezkedik el az elemünk. Ezért a szülő pointerre is szükségünk van. A rákövetkezőt kulcsösszehasonlítások nélkül megtalálhatjuk.

$inorderNext(p : Node3^*) : Node3^*$

Mindegyik műveletre igaz, hogy $MT(h) \in \Theta (h)$, ahol $h$ a fa magassága.

$q := p \rightarrow right$

$q \neq \emptyset$

$q \rightarrow left \neq \emptyset$

$q := p \rightarrow parent$

$q := q \rightarrow left$

$q \neq \emptyset \land q \rightarrow left \neq p$

$p := q; \space q := q \rightarrow parent$

$\text{return} \space q$

Az alábbi feladatok a gyakorlatokon elvégzendő kötelező, illetve gyakorló feladatok.