Szükséges előismeret: Függvények aszimptotikus viselkedése, Jelölések
Algoritmusok és adatszerkezetek 2. > Tömörítés > Tömörítés bevezetés
Tömörítés bevezetés (Compressions)
Ez az oldal egy gyakorlati jegyzet, amelynek anyagára a saját gyakorlati óráimat is építem. Fontos azonban, hogy vizsgára ne kizárólag ebből készülj!
Az elmúlt időszakban többször előfordult, hogy hallgatók az oldalon található anyagból készültek a vizsgára, és emiatt bizonyos feladatokra nem kaptak pontot. Ennek oka, hogy az itt szereplő anyagokat a tantárgyfelelősök nem ellenőrizték és nem lektorálták, így előfordulhatnak benne pontatlanságok, illetve olyan megfogalmazások vagy megközelítések, amelyek nem feltétlenül egyeznek a vizsgán elvárttal.
Az oldalt szabadidőmben készítettem azzal a céllal, hogy segítsem a hallgatók tanulását. A tartalom összeállítását hosszas anyaggyűjtés, könyvek és egyéb szakmai források áttekintése előzte meg, ennek ellenére hibák természetesen előfordulhatnak.
Folyamatosan igyekszem javítani a hibákat és pontosítani az anyagot.
Az informatikában a kódoláselmélet adatok különböző reprezentációjával és azok közötti átalakításokkal foglalkozik. A kezelt adatok mennyisége rohamosan növekszik. A hatékony tároláshoz és átvitelhez az adatok tömörítés szükséges.
A kódolás során fontos kérdés, hogy az adat teljes egészében visszaállítható-e. Tömörítés esetében ennek megfelelően használhatunk veszteségmentes vagy veszteséges eljárásokat (pl. JPEG, MPEG, MP3). Mi csak az előbbivel foglalkozunk.
A kódoláselméletnél meg kell adnunk az információ alapegységét, azaz azt, mennyi információtartalma van az atomi tárolási egységnek. Mivel a jelenlegi számítógépek bináris elven működnek, ez $r = 2$ és így a kódszavaink a $\Gamma = \{'0', '1'\}$ ábécé feletti szavak lesznek. Kódnak nevezzük a $\Gamma$ feletti véges szavak (kódszavak) egy tetszőleges nem üres halmazát.
Egy kód szemléletesebb ábrázolásához elkészíthetjük annak kódfáját. Ebben a fában a fa csúcsai szavak (nem feltétlenül kódszavak), az éleit pedig a kódszavak lehetséges karaktereivel címkézzük. A fa gyökerében az üres szó szerepel és egy szóhoz tartozó csúcs leszármazottai azok a szavak, amelyeket úgy kapunk, hogy a szó után írjuk az élen szereplő karaktert. A kódhoz tartozó kódfa az a legkevesebb csúcsot tartalmazó ilyen tulajdonságú fa, ami tartalmazza az összes kódszót.
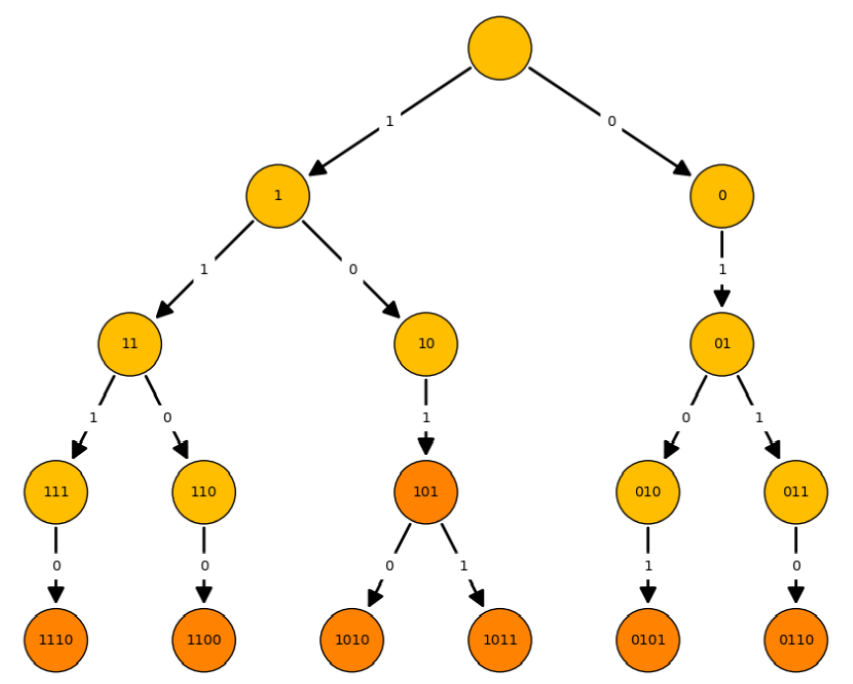
A kódfa segítségével egy bitsorozat hatékonyan dekódolható. A gyökérből indulva a bitek szekvenciájának megfelelően járjuk be a fát, az élek mentén kódszót keresve és a bejárást ismételgetve megkapjuk a dekódolt adatot. (Ha a dekódolás lehetséges és egyértelmű.)
A kódolást betűnkénti kódolásnak nevezzük, ha az eredeti $\sum$ abc feletti adatot betűnként egy $\sum \longrightarrow T \subset \Gamma^*$ kölcsönösen egyértelmű (bijektív) leképezéssel készítjük el. Egy kódot egyenletes kódnak nevezünk, ha a kód szavainak hossza egyenlő.