Objektumorientált programozási szemlélet tanítása Logo-val
1. Pedagógiai megfontolások
A matematika tantárgy nem kellően megfelelő tanítása nem az egyetlen, de a legeklatánsabb példája annak, hogyan alakulhat ki a diákokban a matfóbia. A matfóbia kifejezést, most Papert [1] után, mint valamilyen nehéznek tűnő ismeretrendszertől való iszonyodást alkalmazzuk. Bármely tantárgynál - a kimondottan örömtantárgyként indult informatikánál is - kialakulhat ez az ellenérzés. A tanulmányok kezdetén ez igen károsan befolyásolja a további fejlődést, felsőoktatásban pedig már gyakran gyógyíthatatlan. A megelőzés módja az egyes tantárgyak megszerettetése. Ezt, a megkedveltetést fontosabbnak tartjuk, mint magát a tanítást. Nem feledve, sőt magasztalva a pedagógus jelentős szerepét a tanulás folyamatában, hangoztatjuk, hogy a tanulás végső soron individuális tevékenység, önálló munka, amelyet a tanulónak kell elvégeznie. Papert is az önálló próbálkozásokkal végzett tanulást részesíti előnybe, a konstruktivista tanulást helyezi előtérbe, csupán a megfelelő környezet megteremtését várja a tanártól. Hasonlóan gondolkodik Zsolnai is, a magyar pedagógia kiváló tudósa: "Valóságosan pedig tudjuk, hogy csak az számít, amit önmagunk, önállóan tanulunk meg. Csak azt tudjuk hasznosítani. (Persze ez a felfogás nem jelenti azt, hogy a segítő, beavatkozó, megvilágító, >>fölvilágosító<< tanítói, tanári szónak nincs jelentősége abban, hogy a tanuló valamit megértsen. De ez nem több mint motiváció, mint arra való >>biztatás<<, hogy te magad, aki valamit meg akarsz tanulni, csak úgy tudod birtokba venni a megtanulandót, ha önállóan oldasz meg feladatokat, gondolsz végig problémákat.)" [2]
A számítógépről bizton állítjuk, hogy ma már egy nélkülözhetetlen eszköze az önálló tanulásnak. Nem csak az információk keresése, rendezése terén hasznos, de talán még nagyobb értéke, hogy kísérleti eszköz a diák kezében, a gondolkodásfejlesztés taneszköze, gondolati kísérletek laboratóriuma. A paperti-differenciálmű (gondolati fogódzó, asszociációs alap) ezernyi fajtáját testesíti meg. A tanulás – főként az önálló tanulás – új lehetőségeit nyújtja. Papert tényként álltja, hogy " ...children can learn to use computers in a masterful way, and that learning to use computers can change the way they learn everything else" (Papert, [1] 8th page), … a gyerekek mesteri módon képesek elsajátítani a komputer használatát, és ez a tudásuk megváltoztatja minden más irányú tanulásukat.
A számítógépet a tanulásban használni mi főként ezért tartjuk fontosnak. A számítógép azon túl, vagy talán az előtt, hogy az információk megszerzésének, rendszerezésének eszköze, hogy szórakoztató játékeszköz, azért nélkülözhetetlen az oktatásban, mert gondolatkísérletek laboratóriuma.
A továbbiakban az általunk bemutatásra kerülő görbék előállítása nem csak esztétikai élményt jelenthet, de a matematikával-számítógéppel való gondolkodásfejlesztés talán figyelemre méltó példája, a számítógép célszerű felhasználásának egyik módja lehet a középiskolai matematika – fizika oktatásában, de a programozástanulásnak is egy lehetséges útja.
Amennyiben a különféle görbéket teknőcök mozgatásával, animálásával hozzuk létre az összefüggéseket, ismereteket magunk fedezhetjük fel. A megértés és az emlékezés annál hatékonyabb minél ősibb ingerekhez kapcsolódik. A teknőcgeometria egyrészt a vizualítás felhasználása révén, a mozgókép hatásával, és talán még hatékonyabban a mozgásélményekhez való kapcsolás révén hatékony. A testszintónia – az a lehetőség, hogy a rajzolás folyamatának egyes lépéseit saját testünk mozgásához kapcsolhatjuk - igen jelentősen segít az algoritmusok megértésében. Talán közismertek már a Logoból a sokszögek, és a kör rajzolásának paperti algoritmusai. (Sokszögek generálása történhet előrehaladás és fordulás ismétlésével. A kör pedig a szabályos sokszög határértéke, ha a szögek száma a végtelenhez tart.) Ezek a mozgások a diákok által is végrehajthatók, átélhetők. Általános konszenzust látunk abban is, hogy a többi matematikai görbe is könnyebben, tartósabban megérthető a teknőcgeometria felhasználásával. Újszerű állításunk pedig az, hogy a különlegesebb (hagyományos eszközökkel nehezebben generálható) görbék még érthetőbbek, még barátságosabbak, ha egyszerű teknőcmozgások szuperpozíciójával állítjuk azokat elő, ha a görbék ontológiáját mutatjuk be.
További jelentős didaktikai előny, hogy a görbét leíró, generáló függvény paraméterei, az utasítás paraméterek, az összetevő mozgást végző teknőcök egyes tulajdonságainak feleltethetők meg, így a görbék transzformációi, a szintonia segítsége miatt, könnyebben megvalósíthatók, vizsgálhatóak, érthetők. A függvényanalízist tesszük játékosabbá, élvezetesebbé.
Ha mindehhez objektumorientált programot használunk, a szerszámkezelés (a felhasznált program használatának) könnyedsége révén az aktuális működtetés kevésbé vonja el a figyelmet a lényegtől, s ugyanakkor célszerű gondolkodási módot, programozási alapkészségeket gyakorlunk.
2. Teknőcgeometriai példák
A továbbiakban bemutatásra kerülő
példákat, Soprunov és Alexandrov [3] valamint Uzi [4] dolgozatai inspirálták. Magam
az első teknőc-drámapedagógiával generált görbéket Portóban ismertettem [5].
Ezek is ösztönözték Foltinowicz-ot a teknőcmozgások szuperponálására [6]. A
nemes vetélkedőt folytatva, egyre több felsőfokú görbét generálunk ezen a
módon, amelyek közül most bemutatunk néhányat. Példáimat MicroWorlds Ex Logo
változattal készítettem, de többször bemutatom az Imagine protokollt is.
2.1. Alapalgoritmus
A teknőcök objektumosztályának egyik
példánya az előhívott teknőc. (Az Imagine vagy a MicroWorlds Ex programban
ikonválasztás után a rajzlap valamely pontjára kattintunk.) Az első
teremtményünk alaptulajdonságait megváltoztathatjuk: például, legyen neve Ádám,
tolla leengedett, színe kék. (Pl. a teknőc „hátizsákját”, „igazolványát” jobb
egérgomb kattintással megnyitjuk, a tulajdonságok űrlapot kitöltjük.) Második
teremtményünket „klónozással” is létrehozhatjuk: clone "Ádám (Imagine
esetén clone "Ádám [] ) A második teknőcnek más lesz a neve, de a többi
tulajdonságát, tolla leengedve, színe kék, örökli Ádámtól. (Íme az öröklés
programozási fogalom példázására egy életközeli példa.) A második teknőcöt
nevezzük el Évának, színét pedig állítsuk pirosra. Harmadik teknőcünket is klónozással
(akár Ádámból, akár Évából) hozhatjuk létre. A neve legyen Káin, színét
változtassuk feketére.
Amennyiben az egyik teknőc, mint objektum metódusa, viselkedési szabálya: folyamatosan run :a, a másiké run :b, és egy harmadiké run :a run :b , az első két teknőc mozgásának nyomvonalai összetevői lesz a harmadik teknőc által bejárt eredő görbének. Jelen példában a harmadik teknőc, Káin tehát utánozza Ádámot is, és Évát is. (Az Imagine programban a teknőchöz tartozó táblázatba azt írjuk be forever [run :a] , az MWLogoban a forever rádiógombbal választható, beírás run :a .)
A teknőcökhöz rendelt
metódusok privát vagy publikus voltát jól érthetően szemlélteti mind a
MicroWorlds Logo, mind az Imagine. Amint a teknőc maga is gondolati fogódzó, a
privát metódus elhelyezésére is van jó gondolati fogódzó, a teknőc hátizsákja.
Ide írhatjuk be azon viselkedési utasításokat, amelyeket csak az adott teknőc
ismer. Jelen példánkban ezek az :a és a :b listák végrehajtására utasító parancsok.
Az :a és :b utasításlisták aktuális értékeit pedig, mivel azokat több teknőc is
fogja használni, célszerűen megadhatjuk ( a make utasítással) nyilvánosan, a parancsmezőben.
2.2. Kör
Ha az egyik teknőc folyamatosan halad, a másik ugyanakkor fáradhatatlanul
forog: make "a [fd 1] make "b [rt 1] a harmadik teknőcünk mozgása, a haladás
és forgás szuperpozíciója körözés. A teknőcök animálása, mozgásuk indítása a
teknőcre kattintással történhet.
Változtassuk a lépés és a fordulás értékeket, írjuk át a
metódusokat make
"a [fd step] make "b [rt slue] , a
lépés (step) és a szögelfordulás (slue) paraméterek értékét pedig egy-egy újabb
típusú objektummal, csuszkával (a step és a slue címkéjű és értékű) állítsuk.
Az állítgatásokkal kikísérletezhető, hogyan függ a kör nagysága, és a körözés
sebessége a két paramétertől.
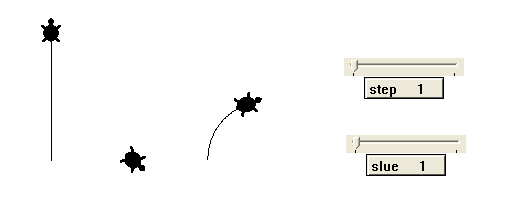
1.ábra Kör, mint két mozgás
eredője
Mivel a kör a
szabályos sokszögek egy speciális fajtája, ezért a sokszögeket is megrajzolhatjuk
ezen ismertetett módon. Pl. négyszöget rajzol Káin, ha a két utánzandó mozgást
a make "a [fd 55] és a make "b [rt 90] paraméter-értékadások alapján
végzi Ádám illetve Éva.
Ha Ádám nem relatív, hanem abszolút koordinátarendszerben mozog, az :a lista értéke forward 1 helyett setx xcor + 1 (Imagineben setxcor xcor + 1) körözés helyett Káin bukfencezik.
2.3. Az indák világa
Amennyiben a két összetevő-mozgás nem állandó sebességű, hanem akár a lépések, akár a fordulások (vagy mindkettő) mértéke változó, akkor spirálokat/indákat kapunk. Az indák világát régóta kutatjuk, logoszerűen csoportosítjuk a spirálokat.
Egyetlen teknőccel így (is) rajzolhatunk spirált:
make
"s 0 repeat 2000[fd 5 rt remainder :s 360 make "s :s + 1]
(Az Imagine nem ismeri a remainder parancsot, de nem is áll le hibaüzenettel, ha a fordulás mértéke 9999 foknál nagyobb, tehát az algoritmusból az Imagine esetén elhagyandó a remainder :s 360.) Változtassuk az :s-t növelő delta értékét! A kapott alakzatokat már sokszor csoportosítottuk, most táblázatba foglaljuk (MW Logo esetén).
A teknőcrózsák csoportosítása – amint ezt már többször publikáltuk – újszerűen, képiesen mutatja be a számokat. Az inda-rajzok „ábrázolják” a számok törzstényezőit. A rajzolat jellegéből látható a szám több tulajdonsága, például, hogy mely számok az osztói. Az ábrák sorából láthatjuk, hogy a számok sorának „pillérkövei” a prímszámok. Az alapmotívum két rózsa. Ebből fúzérek, koszorúk, vagy csokrok alakulnak. Csokrokat akkor kapunk, ha a fordulásérték-növekedés differenciája 5-nél nagyobb prímszám.
|
|||||||||||||||||||||||||||||||||||||||
|
1. táblázat: Az indák világa |
Most a kezdetleges lassú gépek helyett korszerűeket használva újabb kutatási területet találtunk a MicroWorlds Logo használata esetén, hiszen deltának többjegyű számokat is választhatunk, s ilyenkor a régi alakzatainkból újakat "kombinál" a gép, amelyek rajzolásakor periodicitások, ismétlések, és kitörések láthatók. Érdekes ábra ebből a szempontból például a delta = 19630420 értékű, amikor egy teknőc rajzolja meg. Hipotézisünk szerint, itt már a geometria - relatív osztók hatásán kívül a számítógép számolási pontossága is befolyásolja a látványt. A 2. ábra egy ilyen kombinált inda.
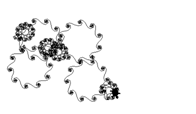
2. ábra Spirál
2.4. Indák szuperpozícióval
2.4.1. Amikor az ábrázolás nem követi a matematikát
Rajzoljuk a spirálokat teknőc-szerepjátékkal! Amennyiben Ádám mozgása továbbra is fd 5, Éva forgása legyen gyorsuló: make "b [rt :s make "s :s + 1] Az :s kezdőértékét pedig állítsuk nullára make "s 0 . Meglepő volt számomra, hogy a szuperpozícióval előállított görbe nem azonos az egy teknőccel generálttal. A MicroWorlds Logo-nál a kétrózsás alapmotívum helyett 14 rózsát kapunk. A továbbiakban ez, a tizennégy rózsa struktúra viselkedik úgy, mint a két rózsa. Az Imagine programnál megint csak (mindkét előbbi körülményekhez képest) általában másfélék az alakzatok, itt még nem találtam szabályosságot. A jelenségre a választ Tomcsányi Péter az Imagine egyik alkotója, EuroLogo konferencián tartott prezentációja alapján állítottam fel hipotézist: Mivel a gépünk egyprocesszoros, a teknőcök csak kvázi paralel dolgoznak. Az összetevő mozgáselemek nem szigorúan váltogatják egymást, s az összegzés is időnként kimaradhat.
2.4.2. Paperti spirál
Spirált kapunk akkor is eredőként (állandó
csatorna keresztmetszetű spirált), ha Éva egyenletesen forog, Ádám pedig egyre
nagyobbakat lép:
A harmadik ábra paraméterei:
make
"s 1
make "a [fd :s make "s :s + 0.1]
make "b [rt 15]
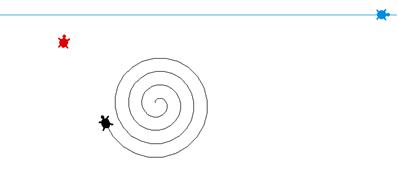
3. ábra Spirál szuperponálással
2.5. Szinusz görbe
Szinuszgörbét egy teknőccel az alábbi
algoritmussal (is) rajzoltathatunk:
to szin :a :n
make "s :a * 3.14 / 180
make "hx 2 * :s / :n / 3.14
repeat 360 * :n
[ask "t4 [fd :s rt 1] ask [t1 t2][setx xcor + :hx] ask [t1 t3][sety ask
"t4 [ycor]]]
end
ahol :a-amplitúdó, :n-periódusszám. Az algoritmust Foltynowicz nyomán írtuk [6]. Ez az eljárás matematikailag komplett, teljes, precíz, elegáns, hagyományosabb stílusú programozással készült. A szin eljárást ezután mintegy apróbb falatokra bontottuk az objektumorientált programozással, a metódusoknak az objektumokhoz rendelésével, a szinuszgörbét így rajzoljuk: A szinusz rajzolásához továbbra is négy teknőcöt szerepeltetünk (Az eddigi Ádám, Éva, Káin triumvirátust kiegészíti Lucifer.)
Lucifer matódusa: örökké fd 1 rt 1
Ádám továbbra is az :a utasítást hajtja végre make "a [setx xcor + 1]
Éva feladata :b végrehajtása, make "b [sety ask "Lucifer [ycor]] Éva tehát Lucifer körmozgásának mindenkori y koordinátaértékét veszi át.
Káin mint eddig végrehajtja :a-t és :b-t . Eredményképpen Káin szinuszgörbét rajzol.

4. ábra. Szinusz újszerűen
Az egyes teknőcök privát metódusai a mozgásutasítások, a teknőcök külön is szerepeltethetők, jól szemléltethető a vezérlő mozgás (Lucifer), a szállítómozgás (Ádám), a relatív mozgás (Éva), és az eredő (Káin). A teknőcök külön-külön tehetik le rajzoló tollaikat, így a négyféle görbéből a kívántat rajzolják. (Célszerűen a teknőcök tollat le, tollat fel utasításokat nyomógombokhoz rendelhetjük.) Ez a példa az objektumorientált programozás azon állítását, amely szerint az objektumok kommunikálnak egymással szemléletesen példázza, hiszen Éva átveszi, elkéri Lucifer y koordinátáját.
A szinusz ontológiája után, látványosan szemléltethető a szinuszgörbe transzformációija, a paraméterek változtatásának hatása. Ez egy-egy összetevő-mozgás változása révén (az episztemológia hatása miatt) jobban érthető.
2.6. Szinuszgörbék összegzése.
Amennyiben négy teknőcünk az előbbiek szerint szinuszgörbét generál, további másik négy pedig egy ezzel párhuzamos másfajta szinuszgörbét, kilencedik teknőcünk egy descarti koordinátarendszerben megrajzolhatja a két szinuszgörbe azon szuperpozícióját, amikor is az y1 és y2 koordinátaértékeket összeadjuk. Így tudunk szinuszgörbére szinuszt illeszteni.

5. ábra. Szinusz + szinusz
Az ábra rajzolásához az egyes teknőc-szerepek:
t1 metódusa run :a halad az x tengely mentén
t2 run :b harmonikus mozgást végez
t3 run :a run :b szinuszgörbét rajzol
t4 run :c köröz
t5 run :aa t5 mint t1
t6 run :bb t6 mint t2
t7 run :aa run :bb t7 mint t3
t8 run :cc t8 mint t4
t9 run :e az eredőgörbét rajzolja
A változók értékei:
make "a [setx
xcor + .1 * step]
make "b [sety
ask "t4 [ycor]]
make "c [fd
amplitudo rt 1]
make "aa
[setx xcor + .1 * step]
make "bb
[sety ask "t8 [ycor]]
make "cc [fd
speed rt 1.5 * speed]
make "e [setx
ask "t1 [xcor] sety (ask "t3 [ycor]) + (ask "t7 [ycor])]
2.7.
Lissajous görbék
Amennyiben két harmonikus rezgőmozgás egymásra merőleges irányú, e kettő mozgás eredője Lissajous görbe. Ezt Foltynowicz példásan modellezte teknőcökkel [6].
Középiskolás szinten ezt egyszerűbben mutatjuk be, a Lissajous görbe létrehozását egyszerűbben is megfogalmazzuk: Két teknőc egy-egy körmozgás függőleges illetve vízszintes vetülete szerint mozog. E két teknőc nyomvonalának szuperponálása Lissajous görbe.
A jelenet szereplőinek (Ádám, Éva, Káin, Lucifer, Lili) feladatai és metódusai tehát:
Ádám átveszi Lili körmozgásának mindenkori x koordinátáját: setx ask "Lili [xcor]
Éva átveszi Lucifer körmozgásának y koordinátáit: sety ask "Lucifer [ycor]
Káin koordinátáit Ádámtól és Évától kapja: setx ask "Ádám [xcor] sety ask "Éva [ycor]
Ádám korábbi példákban egyenletesen egyenesen haladt, most Lili hatására harmonikus mozgást végez. Éva és Káin szerepe a szinusz-jelenthez képest nem változik.
Nyomógombokkal vezérelve könnyen tudjuk modellünkben váltogatni, hogy a vezérgörbéket, a két körzést; a Lissajous összetevőket, a két harmonikus alternáló mozgást; vagy az eredő görbét lássuk. A két körmozgás paramétereinek, illetve ezek egymáshoz való viszonyának változtatásával pedig különféle görbéket generálhatunk.
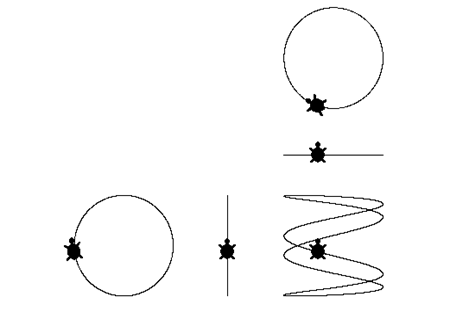
6. ábra. Lissajous görbe
Irodalom
1. Papert, S.: Mindstorms, Basic
Books, New York (1981)
2. Zsolnai József: Vesszőfutásom
a pedagógiáért. Nemzeti Tankönyvkiadó. Budapest (2002)
3. Alexandrov, K. Soprunov, S.: One
Approach to Mechanic Simulations in Logo. In: M. Turcsányi-Szabó (ed.:) Proceedings
Sixth European Logo Conference, Budapest (1997) 114-121
4. Armon, U.: An Algorithm that
Translates Intrinsic Equations of Curves into Intrinsic Procedures of These
Curves. In: M. Turcsányi-Szabó (ed.:) Proceedings Sixth European Logo
Conference, Budapest (1997) 378-389
5. K. Farkas: Logo and native language. Intrinsic
procedures of some curves. In: Secundino Correia (ed.): Proceedings of the
9th European Logo Conference, Porto (2003) 69-79
6. Foltinowicz Izabella
Foltinowicz: Cicloids and limacons in the turtle graphics. Proceddings of the
11th European Logo Conference, EuroLogo 2007, Bratislava Slovakia, 2007.
August. 19-24.