GeoGebra a matematikaoktatásban
Papp-Varga Zsuzsanna
ELTE IK
Absztrakt. A GeoGebra
egy olyan dinamikus matematikai program, mely egyben egy dinamikus geometriai
és egy computer algebrai rendszer. Nagyszerűsége abban rejlik, hogy minden
matematikai objektumnak (pontoknak, egyeneseknek…) megadja mind a geometriai,
mind pedig az algebrai reprezentációját. A reprezentációk között kétirányú a
kapcsolat, egy objektumot módosítva az egyikben módosul a másikban is. A
cikkben bemutatásra kerülnek a GeoGebra alapvető funkciói, oktatásban való
felhasználásnak lehetőségei.
1. Matematikai segédprogramok áttekintése
Bevezetésként
szeretném röviden összefoglalni azokat a szempontokat, amelyeket érdemes
megfontolnia egy oktatónak, amikor arról dönt, hogy mely szoftvert,
szoftvereket használja a matematikaoktatásban.
Léteznek specifikus (kevesebb, kisebb területet érintő)
és léteznek általánosabb célú (több területen is jól alkalmazható) programok. Például
a Graph program csak a függvények témakörével foglalkozik, ezzel szemben a
Maple a matematika szinte minden területét érinti. Találhatók magyar
alkalmazások és olyan külföldiek is, amiknek létezik magyar változata, de
vannak olyanok is, amik csak idegen nyelven érthetőek el. Az Euklidesz például
egy magyar fejlesztésű program, de például a Cabri is kapható magyar fordítással.
A tekintetben is különböznek az egyes szoftverek, hogy milyen szintű
informatikai ismeretek szükségesek a használatukhoz. Léteznek olyan programok
(ilyen például a Derive) amelynek használata csak alapszintű felhasználói
ismereteket igényel és vannak olyanok is, amelyekhez már programozói ismeretekre
is szükség van (ilyen például a Maple vagy a Mathematica). Találhatók olyan
szoftverek, amelyek platform függetlenek és vannak olyanok is, amelyek csak
bizonyos platformokon telepíthetők. Az Euklidesz például csak Windos-on
futtatható, a GeoGebra ezzel szemben Linux-on és Mac OS-on is. Bizonyos
szoftverek oktatási célokra szabadon felhasználhatók, de vannak olyanok,
amelyeknek csak bizonyos verziói érhetők el ingyenesen, sőt olyanok is,
amelyeket csak megvásárolni lehet. A Graph például teljesen ingyenes, az
Euklidesznek csak az 1.1-es változata az, a Maple pedig csak fizetősen érhető
el.
Időtakarékosság szempontjából talán érdemes olyan
szoftvert választani, ami több területen is alkalmazható, így a szoftverrel
való ismerkedésre csak egyszer kell időt szánni. (Természetesen mérlegelni
kell, hogy a többfunkcióságból fakadó esetleges bonyolultság mennyivel nehezíti
meg a program használatát.) A magyar oktatásban javaslom a magyar nyelvű
szoftverek használatát, mert így elkerülhetők az esetleges nyelvi akadályokból
származó nehézségek. (Ez alól azon esetek kivételek, amikor a (szak)nyelv
megtanítása is oktatási cél.) Véleményem szerint általában érdemesebb olyan
szoftvert választani, aminek használata nem igényel magas szintű informatikai
ismereteket, ez alól kivételt képeznek azok az esetek, amikor a magasabb szintű
informatikai ismeretek oktatása, fejlesztése is cél. Azt gondolom, hogy a
közoktatásban fontos szempont, hogy a kiválasztott program ingyenesen elérhető
legyen, hisz így nem csak az iskola költségvetést kíméli a választás, de a
diákok számára is lehetővé teszi az otthoni gyakorlást.
Az általam felsorolt kritériumoknak mind eleget teszt
a későbbiekben bemutatott GeoGebra program, ezért is tetszett meg, amikor
munkám során először találkoztam vele.
2. A GeoGebra program rövid
bemutatása
A
GeoGebra egy ingyenes, platform független, magyar fordításban is elérhető dinamikus
matematikai program. Témájában kapcsolódik a geometriához, az algebrához és az
analízishez.
Középiskolai oktatási segédletként készítette 2001/2002-ben
Markus Hohenwarter a Salzburgi Egyetemen diplomamunkájának részeként. A
matematikaoktatással kapcsolatos doktori tanulmányaiban továbbfejlesztette a
programot. A GeoGebrát az elmúlt évek során számos nemzetközi díjjal
jutalmazták, világszerte több mint 25 nyelvre fordították le. 2006 óta az
osztrák oktatási minisztérium támogatása biztosítja, hogy a szoftver oktatási
célokra ingyenesen felhasználható legyen. A fejlesztés 2006 júliusa óta az
USA-ban a Florida Atlantic egyetemen folyik.
A GeoGebra egyrészt egy dinamikus szerkesztő rendszer.
A felhasználó tulajdonképpen egy virtuális szerkesztőkészletet kap a kezébe,
aminek segítségével elkészítheti a középiskolai szerkesztések bármelyikét. A
papíron végzett szerkesztésektől eltérően viszont itt a kiinduló objektumok
(pontok, egyenesek…) szabadon mozgathatók, úgy hogy a tőlük függő objektumok
velük együtt mozognak.
Másrészt egy computer algebrai rendszer, amiben az
objektumok algebrai úton adhatók meg (pontok koordinátáikkal, egyenesek
egyenleteikkel, függvények képletükkel…). Az objektumokkal különböző
számításokat is lehet végezni, mint például függvények deriválása, integrálása…
stb.
A GeoGebra talán legfontosabb tulajdonsága, hogy egy
kifejezés az algebra ablakban megfelel egy objektumnak a geometria ablakban, és
viszont. Függetlenül attól, hogy az objektumot milyen módon vettük fel (a
geometria ablakban szerkesztéssel, vagy az algebra ablakban paramétereinek
megadásával) mindkét ablakban módosítható és a változás a másik ablakban is
látható.
3. A GeoGebra program használata
3.1.
Indítás
A
program akár telepítés nélkül is futtatható, működéséhez csak JAVA szükséges. A
telepítése se okozhat nehézséget egy alapszintű számítógépes ismeretekkel
rendelkező felhasználó számára. (További információk a http://www.geogebra.org oldal Letöltés
menüpontja alatt találhatók.)
A GeoGebra ablak a Windows-os alkalmazásoktól
megszokott felépítésű: az ablak tetején egy menüsor, alatta pedig egy
eszközkészlet található. A menüben érhetők el azok a funkciók, amik a szerkesztést
globálisan érintik. Az eszközkészlet segítségével tud a felhasználó új
objektumokat felvenni a jobb oldalon található geometria ablakban, amelyek algebrai
paraméterei (koordinátái, egyenletei,) párhuzamosan a bal oldali algebra
alakban láthatóak. Az objektumok természetesen utólag is módosíthatók mindkét
ablakban. Az objektumok az ablak alján található parancssorba beírt parancsok
segítségével is megadhatók, módosíthatók.
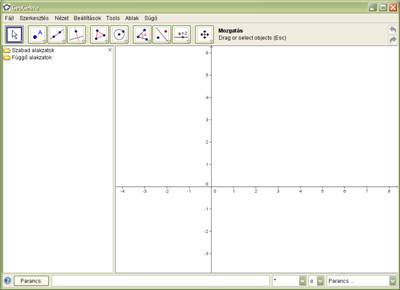
1. ábra: A GeoGebra ablak
3.2.
Alapfunkciók
A
program összes funkciójának, lehetőségének bemutatása egy könyvet is betöltene,
ezért néhány példán keresztül csak a legalapvetőbbeket szeretném ismertetni.
3.2.1. Geometria
Geometria
feladatok esetén érdemes a Nézet menüpontban kikapcsolni a Tengelyeket,
valamint elrejteni az Algebra ablakot. Példaként az Euler egyenes szerkesztését
és a háromszög speciális pontjainak és vonalainak vizsgálatát szeretném
bemutatni.
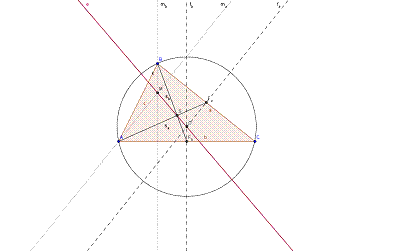
2. ábra: Háromszög speciális pontjai, vonalai
(Euler-egyenes)
Első lépésként fel kell venni egy háromszöget. Ehhez
először ki kell választani az eszközsor Sokszög 
gombját, majd egy-egy egérkattintással meg
kell határozni a háromszög csúcsainak helyzetét, végül pedig a háromszög
elsőként megadott csúcsára kell kattintani. Ekkor a program rögtön el is nevezi
a csúcspontokat, az oldalakat és a háromszöget is (melynek területe látható az algebra
ablakban). Az objektumok tulajdonságai igény szerint módosíthatók a környezeti
menüjükből elérhető Tulajdonság ablakban. A következő lépésben az eszközsor Merőleges
gombjával a felhasználó könnyedén
megrajzolhatja a magasságvonalakat, az adott oldalra majd a szemközti csúcsra
kattintva. A szakaszfelező merőlegeseket a Szakasz felező 
funkció segítségével az oldalakra kattintva
lehet megrajzolni. (A szokványos jelölésben használt alsó indexeket GeoGebrában
is meg lehet adni a „_” jel segítségével.) Az O és M pontokat a Két alakzat
metszéspontja 
gombbal lehet meghatározni, a megfelelő
egyenesekre kattintva. Ekkor már megrajzolható az M és O pontra illeszkedő
Euler egyenes az Egyenes két ponton át 
gomb segítségével. Az alábbi két ábra
illusztrálja, hogy milyen sokat tud segíteni az ábra átláthatóságában az, hogy
módosítható az egyes egyenesek stílusa.
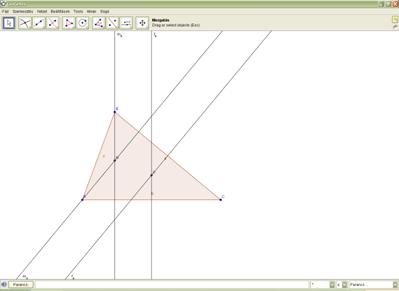
3. ábra: A stílusok módosítása előtt
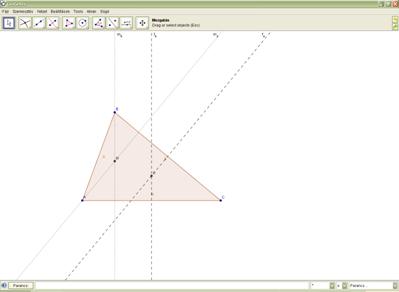
4. ábra: A stílusok módosítása után
A feladathoz most már csak a súlypont helyzetének
meghatározása szükséges, melyet a Felezőpont 
, a Szakasz 
és a Két alakzat metszéspontja funkciók segítségével lehet meghatározni. A
teljesség kedvéért a körülírható kör is megjeleníthető az ábrán (a Kör
középponttal és kerületi ponttal 
funkcióval adható meg az O majd az A pontra
kattintva).
A diákok a háromszög csúcspontjainak mozgatásával
megvizsgálhatják, hogy milyen a speciális pontok, egyenesek relatív helyzete a
háromszöghöz és egymáshoz képest. (A programban arra is van mód, hogy két
alakzat kapcsolatát ne csak geometriailag sejtsük meg, hanem lekérdezzük a
Kapcsolat alakzatok között 
gomb segítségével.) Árki Tamás cikkében [4.]
egy rokon téma a Feuerbach-kör számítógéppel segített tanításával kapcsolatban
további módszertani tippeket találhat az Olvasó.
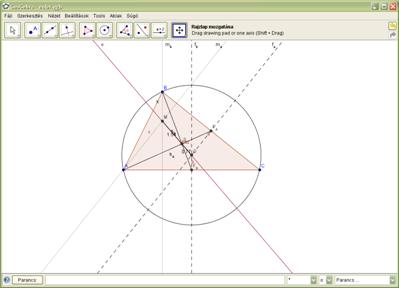
5. ábra: Az Euler egyenes
Természetesen az előbbi példánál nehezebb,
összetettebb feladatok megoldására is képes a program, mint például László
István és Simon Péter „Az Euklides dinamikus geometriai szerkesztőprogram” [5.]
cikkében említett Simson-egyenessel kapcsolatos feladat.
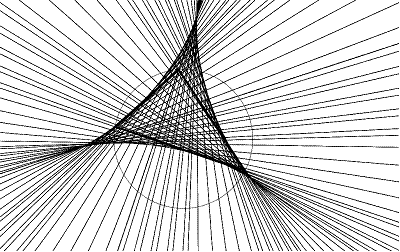
6. ábra: Simson- egyenesek ábrázolása GeoGebrával
3.2.2. Koordináta-geometria
Koordináta-geometria
feladatok esetén az előzőektől eltérően érdemes a Nézet menüpontban bekapcsolni
a Tengelyeket, valamint megjeleníteni az Algebra ablakot. Első példaként az előző
példát szeretném folytatni. A fenti módosításokat megtéve, megvizsgálható, hogy
a súlypont koordinátái hogyan határozhatók meg a csúcspontok koordinátáiból.
Második példaként a kör egyenletének tanításakor jól alkalmazható segédanyag
elkészítését szeretném megmutatni.
Első lépésként fel kell venni a kör középpontját az Új
pont 
funkció segítségével, a rajzlapon tetszőleges
helyre kattintva. Majd meg kell határozni a sugarat, a parancssorba beírva egy
nevet és egy értéket (például r=5). Az algebra ablakban az előbb megadott szám
környezeti menüjében beállítva az alakzat megjelenítését, a geometria ablakban
egy csúszkán változtatható lesz az értéke. Végül pedig a Kör középponttal és
sugárral 
funkciót kell kiválasztani és először a középpontot,
majd a sugarat megadni. Ezt követően az algebra ablakban megjelenik a kör
képlete, a geometria ablakban pedig a képe.
A középpont és a sugár változtatásával párhuzamosan
változó képlet alapján a diákok kitalálhatják, vagy ellenőrizhetik, hogy a
képlet hogyan határozható meg.
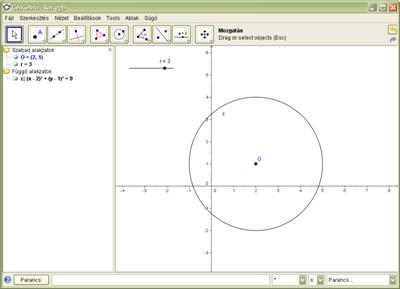
7. ábra: A kör egyenlete
3.2.3. Analízis
A függvények témakörének tanításában is sok segítséget
nyújthat a GeoGebra. Elsőként egy a lineáris függvényekkel kapcsolatos
munkalapon keresztül szeretném megmutatni, hogy milyen egyszerűen készíthetünk
olyan anyagokat, amik megkönnyítik a függvény transzformációk megértését. Dr. Karl
Josef Fuchs írt cikkében [3.] a készítsd grafikusan elvről, melynek kapcsán „a
tanulók egyrészt nagyon könnyen tudják transzformálni a (valós függvények) grafikonjait,
másrészt koncentrálni tudnak a matematikai objektumok központi tulajdonságaira”.
Ezt
követően pedig egy másik munkalapon azt szeretném megmutatni, hogy hogyan nyújthat
segítséget a GeoGebra egy teljes függvény-vizsgálathoz.
Az első munkalapon az ax+b függvény kerül ábrázolásra
tetszőleges a és b értékek esetén. Az elkészítéséhez összesen három parancsra van
szükség. Meg kell adni az a-t és a b-t (például a=1, b=2) és magát a függvényt
(a*x+b). Ezt követően érdemes a-t és b-t megjeleníteni, hogy értéküket a
geometria ablakban lévő csúszkákon könnyedén lehessen változtatni.
A diákok akár új anyag tanulásakor, akár gyakorláskor
sok hasznát vehetik ennek az egyszerű munkalapnak (ami természetesen tovább
csiszolható: címkékkel, szövegekkel…).
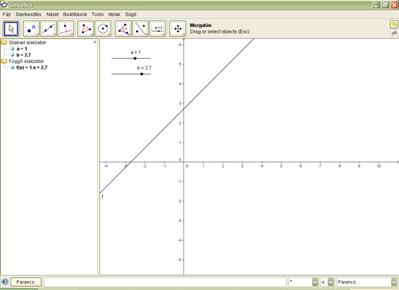
8. ábra: Az ax+b függvény
A második munkalap egy konkrét függvény jellemzéséhez
nyújt segítséget, ízelítőt adva abból, hogy milyen lehetőségeket nyújt a
program. Elsőként be kell írni a parancssorba a függvényt (Parancs: 2*x^3+4*x^2+2).
Egy–egy paranccsal meghatározhatók a gyökei (ZH=gyök[f]), a szélsőértékei (M=szélsõérték[f])
és az inflexiós pontjai (I=inflexiósPont[f]). Amennyiben valamelyik speciális
pontból több is van, a program automatikusan indexekkel látja el a felhasználó által
megadott nevet. A GeoGebra képes meghatározni a függvény deriváltját
(derivált[f]), határozott (Int=integrál[f,a,b]) és határozatlan integrálját
(F=integrál[f]), alsó (Alsó=alsóösszeg[f,a,b,n]) illetve felső közelítő
összegét (Felső=felsõösszeg[f,a,b,n]) is.
Az elkészült munkalap természetesen nem csak egy
függvény elemzésére ad lehetőséget, hiszen a képlet egyszerűen módosítható az algebra
ablakban.
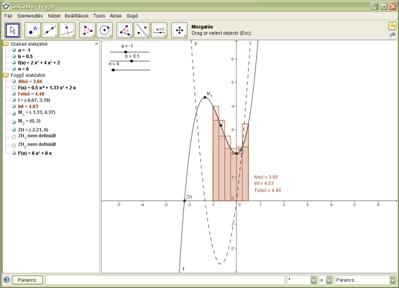
9. ábra: Integrálás
3.3.
Módszertani
szempontból kiemelendő funkciók
Az
előző fejezetben megpróbáltam néhány példán keresztül a legalapvetőbb
funkciókat bemutatni. Most szeretném kiemelni a véleményem szerint módszertani
szempontból érdekesebb funkciókat.
3.3.1. Szerkesztés lejátszása
A
GeoGebra lehetőséget ad a szerkesztések lejátszására. (A Nézet menüben lehet
beállítani, hogy megjelenjen a navigációs eszköztár.) A lejátszás lehet
automatikus, ekkor beállítható a lépések közötti idő, de lehet kézi is, ekkor a
felhasználó lépkedhet egyesével, de elugorhat a szerkesztés elejére vagy végére
is.
A szerkesztőprotokoll segítségével módosítható az
objektumok sorrendje (természetesen az ős objektum meg kell, hogy előzze a
leszármazottat), sőt azt is meghatározható (töréspontok elhelyezésével), hogy
egyszerre több lépés hajtódjon majd végre a lejátszásnál.
Az említett lehetőségek olyan eszközt adnak a tanárok
kezébe, amellyel könnyedén tudnak szerkesztéseket, bizonyításokat, feladat
megoldásokat megmutatni, elmagyarázni.
3.3.2. Megjelenítés
Már
a példákban is többször használtam a csúszkákat, amelyek egy-egy szám geometria
ablakbeli megfelelői. Ezek segítségével, ahogy például a lineáris függvények
esetében mutattam, pillanatok alatt készíthető látványos animáció.
A Nézet menüpontban, mint már említettem be lehet
állítani, hogy láthatóak legyenek-e vagy sem a tengelyek és az algebra ablak.
Hasonlóan elrejthetők, illetve megjeleníthetők a segédvonalak (rács) is. A
Beállítások menüpontban pedig meghatározható, hogy mi legyen a szögek egysége,
a pontok, és a tengelyek stílusa, mi legyen a tengelyeken az egység… stb. Ezt
azért tartom jónak, mert így az aktuális oktatási cél határozhatja meg, hogy mi
legyen látható a munkalapon.
3.4.
Segédanyagok készítése
szempontjából hasznos funkciók
Segédanyagok
készítésekor gyakran ütközhet a készítő bosszantó technikai akadályokba: hogyan
lehet beszúrni az elkészült ábrát egy dokumentumba, hogyan publikálható az
animáció… stb. A GeoGebrával szerencsére könnyedén legyőzhetők ezek az
akadályok. A rajzlap egyszerűen másolható a vágólapra, de menthető képként, sőt
PSTricksként is. A munkalap exportálható dinamikus weblappá. Az exportálás
során többek között az alábbi információk adhatók meg: szerző, cím, dátum,
szerkesztés előtt és után megjelenő szöveg, így könnyedén készíthető - honlap
szerkesztési ismeretek nélkül is – kompakt segédanyag.
Az előbbiekhez képest apróságok, de hasznosak a
Beállítások menüben található Pontelfogás és Betűméret. A Pontelfogás
segítségével csak rácspontokba tudunk pontokat elhelyezni, a Betűmérettel pedig
beállítható a program összes betűjének mérete.
4. A GeoGebra használata a
matematikaoktatásban
Ebben
a fejezetben szeretném összefoglalni, hogy mi mindenre használható a GeoGebra
az oktatásban, milyen területeken nyújthat segítséget a tanároknak és a
diákoknak.
Elsőként azt említeném meg, hogy milyen fontosnak tartom
a diákok motiválását, érdeklődésének felkeltését. A jó pedagógusok
természetesen a számítógépek elterjedése előtt is tudták motiválni a
gyerekeket, nem volt szükségük különböző szoftverekre, így joggal merülhet fel
az Olvasóban a kérdés, hogy akkor most miért lenne szükséges a különböző szoftverek
használata? Elsősorban, azóta sokat változtak a tanítványok, hiszen a
körülöttük lévő világ is nagyot változott. Másodsorban, ezek a programok is
csak részei az eszköztárnak, amiket viszont nem érdemes kihagyni, hiszen olyan
lehetőségeket adnak, amelyek más eszközökkel csak részben vagy egyáltalán nem
érhetőek el.
A motiváláson kívül egy másik fontos feladat a
differenciálás, amelyben nagy segítséget nyújthatnak a különböző szoftverekkel
készített segédanyagok.
GeoGebrában az animációk, a változtatható paraméterek
segítségével a diákok könnyebben megsejthetik, megérthetik, vagy beláthatják az
összefüggéseket. A tanárok gyorsabban, de ugyanakkor hatásosan a lényeget
kiemelve ismételhetnek át különböző témaköröket az órán. A tanárok
segédanyagaikhoz látványos ábrákat készíthetnek a GeoGebra segítségével,
dinamikus munkalapjaikat könnyedén publikálhatják az internet, elérhetővé téve
azokat diákjaik számára. A gyakorló pedagógusok munkáját megkönnyítheti, hogy a
program segítségével könnyedén tudják egy feladat adatait úgy megadni, hogy az
eredmény „szép” legyen. A program segítségével a diákok és a tanárok is
könnyedén ellenőrizhetik az eredményeiket.
5. A GeoGebra támogatása
A
GeoGebra világszerte ismert program ezt bizonyítja az is, hogy számtalan
nyelvre lefordítottak. Nem csak a program érhető el különböző nyelveken, hanem
a Help, a program weboldala is, ahol számtalan hasznos információ található. A
fordításokat lelkes önkéntesek végzik a honalapról letölthető leírások alapján.
Sok tanár számára okoz problémát az, hogy nincs elég
ideje újabb és újabb munkalapokat készíteni. Nagy segítséget nyújthat számukra,
a GeoGebra wiki, ahonnan bárki tölthet le GeoGebrával készített segédanyagokat,
amit aztán kedve szerint felhasználhat a munkájában. A wikit regisztráció után
bárki szerkesztheti, bővítheti. Pár hete jött létre a wiki magyar változata,
ahol egyre több magyarnyelvű segédanyag érhető el.
A program és a segédanyagok önmagukban azonban nem
elegek ahhoz, hogy ennek a remek eszköznek a használata beépüljön a mindennapi
oktatásba, ezért világszerte GeoGebra intézetek hoznak létre, amelyek a tanárok
továbbképzésére hivatottak. Magyarországon egyelőre kevés ember ismeri a
programot, de remélhetőleg majd itthon is lesznek olyan akkreditált
továbbképzések, ahol az oktatók megismerkedhetnek a szoftverrel.
6. Zárszó
Remélem,
hogy a fenti ismertető az Olvasót is meggyőzte arról, hogy a matematika
tanároknak érdemes megismerkednie a GeoGebra programmal, hogy használhassák azt
munkájuk során.
Irodalom
1.
Markus Hohenwarter (Fordította: Sulik Szabolcs): GeoGebra 2.5
kézikönyv (2006)
http://www.geogebra.org/help/docuhu/
2.
Markus Hohenwarter, Judith Preiner: Dynamic Mathematics with
GeoGebra (2007)
http://www.maa.org/joma/Volume7/Hohenwarter/index.html
3.
Dr. Karl Josef Fuchs: Számítógépes algebrai rendszerek a
matematikaoktatásban - Tanárképzési Programok, Kihívások és Új Célok (2002)
http://matserv.pmmf.hu/anniv/cd_hun/prezentaciok/fuchs.pdf
4.
Árki Tamás: A Feuerbach-kör tanítása számítógép segítségével
http://www.sulinet.hu/tart/fcikk/Kcn/0/22581
5.
László István, Simon Péter: Az Euklides dinamikus geometriai szerkesztőprogram
(2002)
http://matserv.pmmf.hu/anniv/cd_hun/prezentaciok/laszlosimon.pdf