Véletlen permutáció előállítása

Az alábbi algoritmusban X(1..N) tömb elemeinek egy véletlen permutációját állítjuk elő. Természetesen elvárjuk, hogy a HalmazFelsorolás(X) előfeltétel teljesüljön.

Talán első hallásra meglepő lesz az ötlet: induljunk ki a permutációgenerálás algoritmusának elkészítésénél a rendezésből. A következő (P1.) algoritmust pl. a minimumkiválasztásos néven ismert rendezésből eredeztetjük.

P1. Algoritmus:

Permutálás („Keverés”)	Rendezés
Ciklus i=1-től N-1-ig j:=VéletlenSzám(i..N) Csere(X(i),X(j)) Ciklus vége	Ciklus i=1-től N-1-ig j:=MinIndex(i..N) Csere(X(i),X(j)) Ciklus vége

Jelölések:

X – sorozat; X’ – az X sorozat algoritmus végrehajtás utáni értéke

P(X’₁=X_j1,…,X’_i=X_ji) – annak a valószínűsége, hogy az algoritmusbeli ciklus i. lépése után az X’_1..i lesz.

P(X’_k=X_j) – annak a valószínűsége, hogy az algoritmusbeli ciklus k. lépése után az X’_k X_j lesz. Az algoritmusbeli ciklus k. lefutása után az X’_k már nem tud változni, így egyszerűen azt is mondhatnánk, hogy az algoritmus végén az X’_k=X_j teljesül.

i,jÎN, aÎ[0,1]ÌR

VéletlenSzám(i..j) – (egyenletesen) véletlen egész szám Î[i,j].

VéletlenSzám – (egyenletesen) véletlen valós szám Î[0,1)ÌR.

Feltevések – egyenletesség:

F1. P(VéletlenSzám(i..j)=k)=P(VéletlenSzám(i..j)=m) k,m=i..j

F2. P(VéletlenSzám<a)=a

Lemma:

P(VéletlenSzám(i..j)=k)=1/(j-i+1) k=i..j

Bizonyítás:

Az i és a j között j-i+1 féle érték van, tehát ezek közül valamelyik kijövetelének valószínűsége biztos esemény (1); és P(1)=1; továbbá egymást kizáró események

Þ

P(VéletlenSzám(i..j)=k)=1 .

Az 1. feltevés miatt ez a j-i+1 esemény egyenletesen osztozik az 1 valószínűségen.

Ebből már adódik az állítás.

Qed.

Például:

P(VéletlenSzám(1..N)=k)=1/(N-1+1)=1/N

P1-1. Állítás:

A P1. algoritmus a bemeneti sorozat egy permutációját állítja elő.

Bizonyítás:

1. a kimeneti állapot hossza megegyezik a bemenetiével,

Mivel az X sorozat változása csak elemeinek helycseréjét jelenti, ezért

2. új elem az eredménysorozatba nem kerül,

3. minden eleme a sorozatban marad.

Þ "iÎ[1..N]: X’_iÎX

Qed.

P1-2. Állítás:

Az X’ minden elemében az X bármely eleme azonos eséllyel lesz a P1. algoritmus végrehajtása után: P(X’_i=X_k)=1/N "i,kÎ[1..N]. (Előfeltétel: X_i≠X_j i≠j, vagyis HalmazFelsorolás(X)=Igaz.)

Bizonyítás:

Indukcióval bizonyítunk: belátjuk, hogy

(i=1) P(X’₁=X_k)=1/N "kÎ[1..N]
(azaz bármelyik elem azonos valószínűséggel kerülhet az első helyre)

(iÞi+1) P(X’_i+1=X_k)=1/N "kÎ[1..N]
(azaz bármelyik elem azonos valószínűséggel kerülhet az i+1. helyre)

feltéve, hogy

(a) P(X’_j=X_m)=1/N "jÎ[1..i],mÎ[1..N]
(azaz bármelyik elem azonos valószínűséggel kerülhet az i.-re vagy
az előtti helyre) és

(b) X’ÎPerm(X) © (X’ a ciklus egyszeri lefutása után X-et jelöli)

(i=1)

A csere juttathat elemet valahova, pl. X’₁–be X_k-t, –az algoritmus szerint– a ciklus i=1 esetében (máskor nem!), amikor a VéletlenSzám(1..N) éppen k-t eredményez. Ennek (P(X’₁=X_k)) a lemma szerint 1/N az esélye. Sőt a csere miatt ugyanekkor nyilvánvalóan az is igaz, hogy P(X’_k=X₁)=1/N "kÎ[1..N].

(iÞi+1)

Indukciós feltételként feltesszük (a)-t.

A továbblépés csak akkor értelmes, ha teljesül (b). Ez viszont az algoritmusból azért következik, mert az elemek legfeljebb helyet tudnak cserélni, de egyéb módon megváltozni nem, azaz az elemek permutálódhatnak csupán.

Meghatározzuk annak valószínűségét, hogy egy elem az i+1. helyre kerüljön. Az alábbi két esemény fennállásának valószínűségét kell meghatározni:

· nem került az 1..i helyek egyikére sem (=1–i/N) és

· a „maradékok” (N-i) közül épp őt sorsolta ki cserére (=1/(N–i))

Vagyis (1–i/N) * 1/(N–i) = (N–i)/N * 1/(N–i) = 1/N

(

Belátandó, hogy P(X’₂=X_k)=1/N "kÎ[1..N].

Két eset van: a k=1 (előbbről került hátrébb) és a K>1.

(k=1)

Ez is két módon következhet be. Jelöljük A-val és B-vel ezt a két összetett eseményt.

A = a ciklus i=1 lefutásakor j=j₁≠2, azaz utána: X_j1 X₂ … X₁… ¨

majd
a ciklus i=2 lefutásakor j=j₁, azaz utána: X_j1 X₁ … X₂…

és a másik mód:

B = a ciklus i=1 lefutásakor j=2, azaz utána: X₂ X₁ … X_i …

majd
a ciklus i=2 lefutásakor (ismét) j=2, azaz utána: X₂ X₁ … X_i …

Az események valószínűségei:

P(A)=P(X’₁=X_j1,X’₂=X₂,…X’_j1=X₁,…) *
* P(X”₁=X_j1,X”₂=X₁,…X”_j1=X₂,…)=
=(N–1)/N * 1/N

(Az első tényezőben figyelembe vettük, hogy j₁ N-1 közül választható.)

P(B)=P(X’₁=X₂,X’₂=X₁,…X’_i=X_i,…) *
* P(X”₁=X₁,X”₂=X’₂=X₁,…X”_i=X_i,…)=
=1/N * 1/N

E kettő összege adja a keresett valószínűséget:

P(X’₂=X₁)= (N–1)/N² + 1/N²=(N–1+1)/N²=N/N²=1/N

(k>1)

Az X’₂=X_k akkor nem következhet be, ha a ciklus i=1 esetében az X_k X’₁-be került. Ennek esélye –mint láttuk– 1/N. Tehát 1-1/N=(N-1)/N esélyű választás után a j-be 2..N közül történik az újabb választás, ami a lemma miatt P(VéletlenSzám(2..N)=k)=1/(N-1) esélyű. Vagyis

P(X’₁¹X_k, X’₂=X_k)=(N-1)/N*1/(N-1)=1/N

(i>2)

Belátandó, hogy P(X’_i=X_k)=1/N "i>2, "kÎ[1..N].

…

)

Qed.

P1-3. Állítás:

A P1. algoritmus azonos eséllyel állítja elő az X_1..N elemek tetszőleges permutációját. (Előfeltétel: X_i≠X_j i≠j, vagyis HalmazFelsorolás(X)=Igaz.)

Bizonyítás:

Belátjuk, hogy P(X’=(X_i1,…,X_iN))=1/N! .

P(X’=(X_i1,…,X_iN))=P(X’₁=X_i1) *
P(X’₂=X_i2 | X’₁=X_i1) *…*
P(X’_N=X_iN | X’₁=X_i1 Ù…Ù X’_N-1=X_iN-1)

P1-1. Þ
P(X’₁=X_i1)=1/N

P1-1. & P1-2. & F1. Þ
P(X’₂=X_i2 | X’₁=X_i1)=1/(N-1)
(hiszen csak N–1 közül, azonos valószínűséggel választható a 2.)

…

P1-1. & P1-2. & F1. Þ
P(X’_N=X_iN | X’₁=X_i1 Ù…Ù X’_N-1=X_iN-1)))=1/(N-(N–1))=1/1
(hiszen csak 1 közül választható az N.)

Végülis:

P(X’=(X_i1,…,X_iN))=P(X’₁=X_i1)=1/N*1/(N-1)*…*1/1=1/N!

Qed.

Az elmélet után jöjjön egy csipet gyakorlat! Győződjünk meg arról, hogy a fentiekben belátott „egyenletesség” a permutációk terében, mennyire és milyen számú permutációgenerálás után mutatható ki.

Írjunk programot, amely a P1. eljárással előállít számos permutációt, s eközben számolja, hogy az éppen generált permutáció hányadszorra jött ki. Azt várjuk, hogy minden permutációra ez kb. azonos érték lesz.

Mivel a permutációk száma N!, ezért

1. ahhoz, hogy elvileg minden permutáció létrejöhessen: legalább N!-szor kell az eljárást meghívni;

2. a számláló tömbnek is N! eleműnek kell lennie (a legszorosabban számolvaª). Pl. 8!= =40320, ami már a Turbo Pascal memóriában tartott tömbjének a méretét meghaladja.

Segíthetünk ez utóbbi problémás helyzeten, ha építünk a P1-2. állításra. Ugyanis e szerint „elegendő” azt számlálni, hogy az egyes X’-beli elemek gyanánt hány ízben fordultak elő az eredeti X-beli elemek. Vagyis egy N´N-es mátrix is elég a számláláshoz, ha N az X hossza.

1. ábra. A program eredményének magyarázata.
A 7 (N) elemű 7! számú permutációt a P1. algoritmussal generálva azt tapasztaltuk, hogy a generált permutációkban 1. helyen az 1 (X₁) 1452-ször, … a 7. helyen ugyanő 1377-szer fordult elő, … a 7 (X₇) az 1. helyen 1405-ször, … a 7. helyen ugyanő 1440-szer. Ellenőrizhető, hogy mind a sor-, mind az oszlopösszegek 10080 (=2*N!), aminek az az oka, hogy –biztos, ami biztos– ennyi (2*N!) darab véletlen permutációt generáltunk a programmal.

A kiértékelést vezérlő algoritmus nagyjából az alábbi lehet:

Procedure PermutacioVezerles;

Var

i:LongInt;

Begin

PermInic;

For i:=1 to Fakt(N) {esetleg 2*Fakt(N)} do

Begin

VeletlenPermutacio;

PermErtekeles;

End;

GyakorisagMegjelenites('Permutációk');

End;

A VéletlenPermutáció eljárása állítja elő a globálisan elérhető tömbben (legyen ez p:TPermutacio) az új permutációt:

Procedure VeletlenPermutácio;

Var

i,j:integer;

Procedure Csere(Var x,y:byte);

Var

s:integer;

Begin

s:=x; x:=y; y:=s

End;

Begin

For i:=1 to N-1 do

Begin

j:=Random(N-i+1)+i; Csere(p[i],p[j])

End;

End;

A PermErtekeles a gyakoriságokat számláló mátrix (gy:TGyakorisag) megfelelő elemét növeli:

Procedure PermErtekeles;

Var

i:Byte;

Begin

For i:=1 to N do Inc(gy[p[i],i]);

End;

Az egészet lásd egyben: VELKOMB.PAS, illetve működés közben: VELKOMB.EXE.

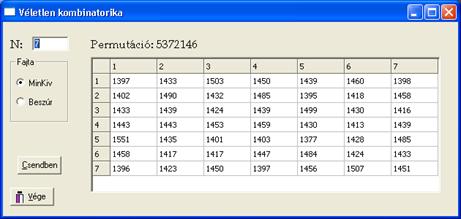
Ugyanennek egy barátságosabb, vizuális (Lazarus) környezetbeli változatának eredményét mutatja a 2. ábra. (Kipróbálhatja: veletlenkombinatorika.exe.)

2. ábra. A Lazarus alkalmazás eredménye.

A következő (P2.) algoritmus beszúrásos rendezés alapgondolata alapján készült.

P2. Algoritmus:

Permutálás („Keverés”)	Rendezés
Ciklus i=2-től N-ig j:=VéletlenSzám(1..i) y:=X(i) JobbraLéptet(X(j..i-1)) X(j):=y Ciklus vége	Ciklus i=2-től N-ig j:=RendezettHelye(1..i) y:=X(i) JobbraLéptet(X(j..i-1)) X(j):=y Ciklus vége

P2-1. Állítás:

A P2. algoritmus a bemeneti sorozat egy permutációját állítja elő.

Bizonyítás:

A P1-1. bizonyításához hasonlóan.

Qed.

P2-2. Állítás:

Az X’ minden elemében az X bármely eleme azonos eséllyel lesz a P2. algoritmus végrehajtása után: P(X’_i=X_k)=1/N "i,kÎ[1..N]. (Előfeltétel: X_i≠X_j i≠j, vagyis HalmazFelsorolás(X)=Igaz.)

Bizonyítás:

Belátandó: P(X’_i=X_k)=1/N "i,kÎ[1..N] !

… hf. …

Qed.

P2-3. Állítás:

A P2. algoritmus azonos eséllyel állítja elő az X_1..N elemek tetszőleges permutációját. (Előfeltétel: X_i≠X_j i≠j, vagyis HalmazFelsorolás(X)=Igaz.)

Bizonyítás:

A P2-1. és a P2-2. állítások nyilvánvaló következménye.

Qed.

Ismét a gyakorlat következik: írjunk programot, amely a P2. eljárással előállít számos permutációt, s eközben az előző programhoz hasonlóan adminisztrálja az elemek előfordulásszámát.

3. ábra. A P2. algoritmust megvalósító alkalmazás eredménye.

Véletlen kombináció előállítása

Az alábbi algoritmusok segítségével az 1,2,…,N számok K-ad rendű véletlen kombinációit tudjuk előállítani. (Ez nyilvánvalóan nem jelent megszorítást, hiszen a feltehető halmaztulajdonság miatt egy-egy kapcsolatban áll az elem és indexe.)

K0. Algoritmus:

Db:=0
Ciklus i=1-től K-ig
Ha VéletlenSzám<K/N akkor Db:+1; Y(Db):=i
Ciklus vége

Világos, hogy az algoritmusban K/N eséllyel kerül be egy elem, csakhogy az össz elemszám (Db) eltérhet az elvárt K-tól. M(Db)=K, D²(Db)=N*K/N*(1-K/N)=K-K²/N

K1. Algoritmus:

Db:=0
Ciklus i=K+1-tól N-ig
Ha VéletlenSzám<(K-Db)/(N+1-i) akkor Db:+1; Y(j):=i
Ciklus vége

Az algoritmus kiküszöböli az előbbi hibáját. Azt az elvet alkalmazza, hogy figyeli a még beveendő elemek számát, és garantálja, hogy éppen annyi kerüljön be.

K2. Algoritmus:

Ciklus i=1-től K-ig
Y(i):=i
Ciklus vége
Ciklus i=K+1-tól N-ig
Ha VéletlenSzám<K/i akkor j:=VéletlenSzám(1..K); Y(j):=i
Ciklus vége

K2-1. Állítás:

A K2. algoritmus az {1..N} számok egy K-ad rendű kombinációját eredményezi.

Bizonyítás:

… hf. …

(a P1-1. mintája alapján könnyű)

Qed.

K2-2. Állítás:

A K2. algoritmus végrehajtása utáni X’-re igaz, hogy X’ bármely eleme helyén X bármely eleme azonos eséllyel (K/N) előfordulhat.

Bizonyítás:

Mivel N elem van, és ebből K-nak kell előfordulni X’-ben, azonos eséllyel, ezért tetszőleges elemre az előfordulás valószínűségének K/N-nek kell lennie.

Két esetet kell vizsgálni:

1. i£K,

2. i>K.

Azért érdekes a szétválasztás, mert az első esetbeli i-k az inicializálás során, 1 valószínűséggel kerülnek az eredmény sorozatba, így azt kell belátnunk, hogy K/N valószínűséggel benn is tud maradni egy kiválasztott ilyen i. Ezzel szemben a 2. esetben nemcsak a bennmaradással, hanem a bekerüléssel is foglalkozni kell. Tehát:

1. A K+1. lépésben (bármely) j. (azaz a j értékű) elem bennmaradásának valószínűsége:

(1 – K / (K + 1) ) [azaz a következő adat nem „akarta” kilökni]
+ K / (K+1) * (K–1) / K [azaz a következő adat „akarta” ugyan, de nem sikerült]
= (K+1–K) / (K+1) + (K–1) / (K+1) =
= K / (K+1)

Indukciós feltétel: az L. (>K) lépésben a bennmaradás esélye = K / L.

Indukciós lépés: az L+1. lépésben …:

K / L [az L. lépésig bennmaradt=indukciós feltétel]
* ( ( 1 – K / (L+1) ) + K / (L+1) * (K–1) / K ) =
= K / L * ( (L+1–K) / (L+1) + K*(K–1) / ((L+1)*K) ) =
= K / L * ( (K*L+K-K*K + K*K-K)) / (K*(L+1)) ) =
= K / L * (K*L) / (K*(L+1)) = K / L * L / (L+1) = K /(L+1)

Innen már következik, hogy az N. lépésben a bennmaradás valószínűsége: K / N.

Azaz "i£K: a keresett valószínűség K/N.

2. Az i. lépésben az i bekerülése és az i+1. lépésben bennmaradás valószínűsége:

K / i [bekerülés valószínűsége]
* ( 1 – 1 / (i+1) ) [az adott j elem nem módosulásának valószínsége]§
= K / i * (i+1–1) / (i+1) = K / (i+1)

Indukciós feltétel: az „i. lépésben bekerül i, s az i+L. lépésig a benn is marad” esélye = K / (i+L).

Indukciós lépés: az i+L+1. lépésben …:

K / (i+L) [L.-ig bennvan]
* ( 1 – i / (i+L+1) [„békén hagyták”]
+ K / (i+L+1) * (K–1)/K ) [megpróbálták kilökni, de nem sikerült]
= K / (i+L) * ( (i+L+1)*K – K*K K*K–K) / ( (i+L+1)*K) ) = …
= K / (i+L+1)

Innen már látszik, hogy az N-nel jelölt utolsó lépésben a bennmaradás valószínűsége: K / N.

Azaz "i>K: a keresett valószínűség K/N.

Qed.

K2-3. Állítás:

A K2. algoritmus azonos eséllyel állítja elő az {1..N} számok tetszőleges K-ad rendű kombinációját.

Bizonyítás:

A K2-1. és K2-2. állítások nyilvánvaló következménye.

Qed.

Az elmélet után jöjjön ismét a gyakorlat! Győződjünk meg arról, hogy a fentiekben belátott „egyenletesség” a kombinációk terében, mennyire és milyen számú kombinációgenerálás után mutatható ki.

Írjunk programot (vagy folytassuk az előbbit), amely a K2. eljárással előállít számos kombinációt, s eközben számolja, hogy az éppen generált hányadszorra jött ki. Azt várjuk, hogy minden kombinációra ez kb. azonos érték lesz.

Bár a kombinációk száma jóval alatta marad a faktoriálisnak, ennek ellenére alkalmazzuk a P1. megvalósításánál ecsetelt számláló módszert! Itt a K2-2. állításra építhetünk. Ugyanis e szerint elegendő azt számlálni, hogy az egyes X’-beli elemek gyanánt hány ízben fordultak elő az eredeti X-beli elemek. Vagyis egy N´K-as mátrix is elég a számláláshoz, ha N az X hossza, K a kombináció rendje.

…

4. ábra. A program eredménye (N=7, K=4).

Alkalmazások

Permutációk témakörhöz

Feladat:

N*K elemű halmaz K egyenlő részre osztása véletlenszerűen.

Algoritmus:

Véletlen részekre osztás

Eljárás VélOszt(Konstans X:Tömb(1..N*K:TElem)
Változó H:Tömb(0..K-1:Halmaz(TElem)):
Változó i:Egész
H(1..K):=Æ
Ciklus i=1-től K*N-1-ig
j:=VéletlenSzám(i..K*N); Csere(X(i),X(j))
H((i-1) Div K):+X(i) [’+’=unió]
Ciklus vége
Eljárás vége.

---

© Perm = Permutációhalmaz

¨ Pirossal emeltük ki a cserében résztvevő elemeket.

ª Ugyanis e mögött az a feltevés húzódik, hogy minden egyes permutációhoz kölcsönösen egyértelműen tudunk a (számláló tömb-beli) indexértéket rendelni. Ha belegondolunk, ez nem is könnyű feladat!

§ 1–K/(i+1) [semmi sem kerül be] + K/(i+1)*(K–1)/K [i+1 bekerül, de nem oda ] =
= 1+ (–K + K–1)/(i+1) = 1 – 1/(i+1)