Szövegfeldolgozási
beadandó feladatok

Jó hír: A feladatok egyszerűek!

Rossz hír: A megoldásnak, mint terméknek igényesnek kell lennie!

Ebből következőleg a beadandóval szemben a „megszokottakhoz” képest hangsúly némileg eltolódik, ami maga után vonja a javítási útmutató („Értékelési szempontok” [ESz], „Tematikában” [T] foglaltak) módosulását. Ezt foglaljuk össze az alábbiakban:

A) T/„A beadandóval szemben támasztott feltételek”/1-4. komolyan veendő.

B) ESz/3.2. „Specifikáció…”-hoz: a feladat pontos specifikációját matematikai formalizmussal kell megadni. Erre építendő a dokumentáció teszteléssel foglalkozó része (fekete doboz tesztelés).

C) A pontozási értékek ugyan változatlanok, de egyes szempontok szigorúbban lesznek értékelve („Programkód” – kényelmesség/külcsín; „Dokumentáció” – illusztráltság, „Specifikáció” – formalizáltság, „Algoritmus” – modularizáltság, „Kód” – biztonságosság, modularizáltság).

A feladatok

1. Matematikai szövegek írásánál gyakori a tört. Valósítsuk meg úgy, hogy a tört számlálóját a megfelelő hely feletti, nevezőjét pedig alatti sorba írjuk, az aktuális sorba pedig - jeleket teszünk. ĺgy –általában!– a szöveg három sorra esik szét. A törteket a bemenő szöveg fájlban szokásos módon, /-jellel kell leírni. Könnyítés kedvéért elvárható, hogy a szöveg fájl csak képleteket tartalmaz, soronként egyet-egyet; s a képletekben szóköz csak a tört előtt és után található. Pl.:

Input sor	Output sor
(n-1)* n/2 cos(a)= m/sqrt(m*m+n*n+p+p) lanc(n,1)= 1/n lanc(n,2)= 1/lanc(n,1) = = 1/( 1/n [SzP1] )	n (n-1)*--- 2 m cos(a)=------------------- sqrt(m*m+n*n+p+p) 1 lanc(n,1)=---= n 1 lanc(n,2)=-----------= lanc(n,1) 1 =------- ( 1 ) (---) ( n )

2. Matematikai szövegek írásánál gyakori az indexelés, a hatványozás és a szummázás. Valósítsuk meg úgy ezeket, hogy az indexet a megfelelő érték alatti, a kitevőt a megfelelő érték feletti sorba írjuk. A szummás kifejezések speciális szintaxisúak, amit az alábbi példa definiál. Az eredmény szöveg fájlban tehát minden bemeneti sornak 3 sor felel meg. Az indexeket a bemenő szövegben @-jel, a kitevőket a ^-jel előzi meg, és szóköz zárja le. Pl.

Input sor	Output sor
… A2S = Szumma (i=1..N) a@i ^2 …	N 2 … A2S = Szumma a … i=1 i

3. Készítsen programot, amely egy idegen szöveget tartalmazó szöveg fájl minden magánhangzóját ékezetesíti, illetve –igény szerint– ékezetmentesít! Az ékezetes betűk ékezetmentes alakjukban két karakterrel vannak kódolva, a következőképpen: â=a^, Â=A^, ä=a:, Ä=A:, ă=a˘, Ă=A˘, ë=e:, Ë=E:, î=i^, Î=I^, ń=n', Ń=N', ô=o^, Ô=O^, ý=y', Ý=Y'. Egyéb ékezetes betűk változatlanul hagyandók! Ha a „módosító jelek” bármelyike a szövegben „önmagáért” fordul elő, akkor duplázni kell, s ekkor az átalakítás után is megmarad egy példányban (s természetesen nem módosítja az –esetleg– előtte álló magánhangzót).

Egy példaszöveg:

„Az aposztróf ('') duplázva kell szerepeljen. Ugyanígy a kétféle "kalap" is (^^/˘˘), a kettőspont (::). Átírás szabályának egy részlete: â=a^, Â=A^, ä=a:, Ä=A:, ă=a˘, Ă=A˘, …”

Ez „kódolás” (ékezetmentesítés) után az alábbi:

„Az aposztróf (') duplázva kell szerepeljen. Ugyanígy a kétféle "kalap" is (^/˘), a kettőspont (:). Átírás szabályának egy részlete: a^=a^, A^=A^, a:=a:, A:=A:, a˘=a˘, A˘=A˘, …”

Az utóbbit ékezetesítve kapjuk:

„Az aposztróf ('') duplázva kell szerepeljen. Ugyanígy a kétféle "kalap" is (^^/˘˘), a kettőspont (::). Átírás szabályának egy részlete: â=â, Â=Â, ä=ä, Ä=Ä, ă=ă, Ă=Ă, …”

4. Készítsen programot, amely –igény szerint– egy szöveg fájl minden magánhangzóját ékezetesíti, illetve ékezetmentesíti! Az ékezetes betűk a szövegben két karakterrel vannak kódolva, a következőképpen: á=a', é=e', í=i', ó=o',ö=o:, ő=o", ú=u', ü=u:, ű=u". (A nagybetűkre hasonlók vonatkoznak.) Ha a „módosító jelek” bármelyike a szövegben önmagában fordul elő, akkor duplázni kell, s ekkor kódolás után is megmarad egy példányban (s természetesen nem módosítja az –esetleg– előtte álló magánhangzót)

5. Készítsen programot, amely –igény szerint– egy szöveg fájl minden magánhangzóját ékezetesíti, illetve ékezetmentesíti! Az ékezetes betűk a szövegben két karakterrel vannak kódolva, a következőképpen: á=aa, é=ee, í=ii, ó=oo, ö=oe, ő=oy, ú=uu, ü=ue, ű=uy. (A nagybetűkre hasonlók vonatkoznak.)

6. Készítsen programot, amely egy ékezetes szöveg minden magánhangzóját ékezetmentesíti! Az ékezetes betűket a szövegben két egymás fölötti karakterrel kódolja: az ékezettől függően az ékezet nélküli betű fölé ", ', : jeleket tesz. Tehát a bemenő fájl minden „normál” sora két tényleges sort igényel: egyet az ékezeteknek, egyet az ékezet nélküli magánhangzókat tartalmazó „normál” szövegnek. A program igény szerint a fordított feladatot is elvégzi. Példa a két-sorosból egy-soros átalakításra:

Input sor	Output sor
’ ’ ’ Keszitsen programot, amely –igeny ’ : szerint- ekezetes szoveget …	Készítsen programot, amely -igény szerint- ékezetes szöveget …

7. Készítsen titkosító, illetve titkos szöveget megfejtő programot! A szövegben csak „hétköznapi jelek” fordulhatnak elő: betűk, szám- és zárójelek, illetve a központozás jelei. A titkosírás módszere legyen az, hogy a magánhangzókat magánhangzókkal, mássalhangzókat mássalhangzókra cserélünk; egyebeket változatlanul hagyunk. A cseréhez két –paraméterként megadott– szám tartozik: MaE, MsE. MaE: a magánhangzókra vonatkozó; MsE: a mássalhangzókra vonatkozó eltolási érték. Ezek írják le, hogy mennyivel „odébb levővel” kell helyettesíteni az adott jelet. (Az eltolási értéket ciklikusan kell érteni.)

A program adjon minimális analízist! Azaz a jelek gyakoriságát mind a bemeneti, mind a kimeneti szöveg tekintetében, kis- és nagybetűket meg nem különböztetve.

8. Készítsen titkosító, illetve megfejtő programot! A titkosírás módszere legyen az, hogy a karaktereket helyettesítsük egy –kódoló fájlban tárolt– táblázat szerint más karakterekkel!

A program adjon minimális analízist! Azaz a jelek gyakoriságát mind a bemeneti, mind a kimeneti szöveg tekintetében, kis- és nagybetűket meg nem különböztetve. Ellenőrizni –és hiba esetén jelezni– kell, hogy a kódoló tábla egyértelmű-e! A kódoló tábla jelpárokból (mit-mire kell cserélni) álló sorozat, amelyben a „mit” gyanánt nem szereplő jel változatlan marad a kódolás során.

9. Készítsen titkosító, illetve megfejtő programot! A kódolandó (és a kódolt) szöveg csak „hétköznapi jeleket” tartalmazhat: betűk, szám- és zárójelek, illetve a központozás jelei. (Ez kb. 100 jelet jelent.) A titkosírás módszere legyen a következő:

· Generálja le a megengedett jelek összes két jelből álló variációját. Ez egy kb. 10000-es táblázat: PárTábla.

· A szöveget bontsa fel két jelből álló csoportokra. Az utolsó csoport lehet „páratlan”, ekkor párosítsa a szóközzel.

· Minden csoportot keressen meg a PárTáblá-ban, majd

· helyettesítse egy –paraméterként megadott– K ciklikus eltolási értékkel kijelölt PárTábla-beli jelkettőssel.

A program adjon minimális analízist! Azaz a jelek gyakoriságát mind a bemeneti, mind a kimeneti szöveg tekintetében, kis- és nagybetűket meg nem különböztetve.

10. Készítsen titkosító, illetve megfejtő programot! A kódolandó (és a kódolt) szöveg csak „hétköznapi jeleket” tartalmazhat: betűk, szám- és zárójelek, illetve a központozás jelei. A titkosírás módszere legyen a következő (Vignère):

· Csak betűket kódolunk (dekódolunk), a többi jel transzformálatlanul kerül az outputra.

· Legyen adva egy kulcs-szó (pl. „SzP”), amely jeleinek belső kódja, mint eltolási érték funkcionál. Tudott, hogy a nagy és kisbetűk önmagukon belül egybefüggően foglalnak helyet az ASCII kódrendszerben ('A'®65..'Z'®90, 'a'®97.. 'z'® 122), de közéjük furakodott néhány egyéb írásjel. A számunkra fontos betűk „sajátos kódjait” 1-től, folytonosan kell elképzelni: elől a nagy-, mögöttük a kisbetűket. Pl.: „SzP”Þ(83,122,80), de ABC-kódja (83-65+1,122-97+1+90-65, 80-65+1)=(19,51,16).

· A kódolandó szöveghez illesztjük (természetesen csak képletesen) a kulcsot, s az egyes jeleket pont annyival toljuk el a jeltáblában, amennyi a kulcs mellé eső jelének ABC-kódja. Ha pl. a kulcs adott jele éppen 'A', akkor 1-gyel kell (ciklikusan) léptetni a szöveg mellé eső betűjét; ha 'S', akkor 19-cel...

· Ügyelni kell, hogy betűhöz betű legyen rendelve a kódolás után.

· A program kérdezzen rá, hogy magyar ABC sorrendben vegye-e figyelembe a szöveget, vagy a standard ASCII kódolási sorrend jó-e! Magyar sorrend esetén –jobb híján– az A lesz az 1 kódú éít. Azaz az A mint kulcs pontosan eggyel tolja tovább a transzformálandó betűt. (próba)

Például:

Standard (azaz nem magyar) esetben és „SzP” kulcs mellett az alábbi szövegtranszformációt kapjuk: 'AÁBCaábc' ® 'TÁRVaáuc'

Magyar esetben, ugyancsak az „SzP” kulcs mellett: 'AÁBCaábc' ® 'TÁSÜarúc'.

A program adjon minimális analízist! Azaz az angol betűk gyakoriságát mind a bemeneti, mind a kimeneti szöveg tekintetében, kis- és nagybetűket meg nem különböztetve.

11. Készítsen titkosító, illetve megfejtő programot! A titkosítást (és a megfejtést) egy megfelelő helyen „kilyukasztott” N´N-es négyzetrács felhasználásával kell elvégezni. A szöveget N betűt tartalmazó sorokra tördeljük, és egymás alá rendezzük. Ráhelyezzük a szöveg első, N soros darabjára, és a lyukaknál látható betűket egymásután írjuk. Ezután elforgatjuk 90 fokkal a rácsot, és újból felsoroljuk a láthatóvá vált jeleket. Még kétszer elvégezve a forgatást és betűfelsorolást a rács alá eső szövegrészt rejtjeleztük. 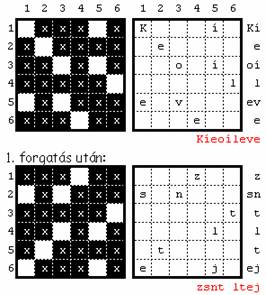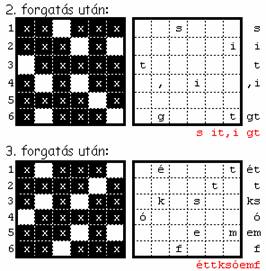Ugyanígy járunk el a maradék szöveggel is. Minden további magyarázkodás helyett lássuk az alábbi példát!

A „kulcs” szerepét betöltő 6´6-os négyzetrácsot a későbbi ábra bal-felső négyzetrácsa mutatja. A titkosítandó szöveg legyen a következő részlet: „Készítsen titkosító, illetve megfejtő programot! A titkosítást (és a meg”. A titkosítás után kapott jelsorozat: „Kíeoílevezsnt ltejs it,i gtéttksóemfőoa íás mrrmtstt epo! oíéag gtAtk(s ”.

Az első 6´6 jelből álló jelsorozatra alkalmazandó lépéseket mutatja az alábbi ábra:

A program beolvassa a rácsot egy mátrix formájában, majd a titkosítandó, illetve megfejtendő szöveget, és elvégzi a kívánt átalakítást. Az világos, hogy a rács nem lehet tetszőleges! Ezért a program legyen képes annak jelzésére is, hogy a rács esetleg nem töltheti be a kulcs szerepét!

12. Készítsen titkosító, illetve megfejtő programot! A titkosítást (és a megfejtést) egy megfelelő helyen „kilyukasztott” N´N-es négyzetrács felhasználásával kell elvégezni, így: A rejtjelzés során egy üres „papírra” helyezzük a rácsot, és a lyukakba írjuk a titkosítandó szöveg jeleit balról jobbra, sorfolytonosan haladva. Majd a rácsot 90 fokkal elforgatva újra elvégezzük a jelek beírását a lyukakba. Így teszünk még kétszer, s a szöveg összes jelét a jelmátrix valamely pozíciójába elhelyeztük. A jelmátrix sorait egymásután írva megkapjuk a szöveg első N´N-es rejtjelezett kódját. Természetesen ezt a szöveg maradék részére is alkalmazzuk.

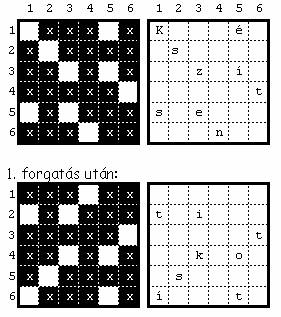
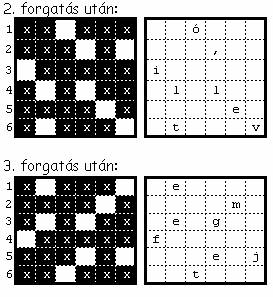
A „kulcs” szerepét betöltő 6´6-os négyzetrácsot a későbbi ábra bal-felső négyzetrácsa mutatja. A titkosítandó szöveg legyen a következő részlet:

„Készítsen titkosító, illetve megfejtő programot! A titkosítást (és a meg”. A titkosítás után kapott jelsorozat:

„Keó é tsi,m iezgítflklotsseeejíttntvő(ko étp!ossí rao tAá grtamseítgmt”.

Az első 6´6 jelből álló jelsorozatra alkalmazandó lépéseket mutatja az alábbi ábra:

És a teljesen feltöltött jelmátrix látszik balra.

A program beolvassa a rácsot egy mátrix formájában, majd a titkosítandó, illetve megfejtendő szöveget, és elvégzi a kívánt átalakítást. Az világos, hogy a rács nem lehet tetszőleges! Ezért a program legyen képes annak jelzésére is, hogy a rács esetleg nem töltheti be a kulcs szerepét!

13. Készítsen programot, amely egy szöveg fájlban előforduló összes hexadecimális számot (amelyek Hxxxx alakúak, ahol xÎ{’0’..’9’,’A’..’F’}) decimálisra, illetve decimális számot hexadecimálisra alakít! Az eredmény fájlban a szám párja (hexának decimális, decimálisnak hexa) szögletes zárójelek között jelenik meg; pl. így „… H00FF …” gyanánt az eredmény szövegben „… H00FF [=256] …” jelenik meg.

14. Írjon konverziós programot, amely képes római számok 10-es számrendszerbeli párjára átalakítani és viszont! Az átalakítandókat egy szöveg fájl tartalmazza az alábbi példa szerint (lásd a programot!):

Input sor	Output sor
MCMXCIX	1999
2002	MMII

15. Írjon programot, amely egy szöveg fájlbeli szöveget átalakít morzejelekké, illetve igény szerint „visszafordít”! (A Morse-abc kódtábláját lásd a mlógia 14 kötet 9. oldalán.)

16. Készítsen programot tükörszavak keresésére! Azaz input fájl sorait végignézi, és elemzi, hogy van-e benne olyan szöveg részlet, amelyet megfordítása követ. Megengedjük, hogy a „szimmetria középpontjaként” tekintett jel egyszeres legyen, sőt kimondjuk: kis- és nagybetűk nem különböznek; továbbá a „szerencsétlenül elhelyezkedő szóközök nem ronthatják el a szimmetriát. Pl.: tükörszavak: „ABBA”, „Aba”, „Indul a görög aludni”.

17. Készítsen programot, amely egy szöveg fájl egyes részeit képes kiemelni (ritkítva, illetve aláhúzva írni). A kiemelendő részeket a szövegben #-, illetve $-jelek közé tettük. Az aláhúzás miatt a konvertált szöveg a kimeneti fájlban két sorosan jelenik meg. (Ha a fenti jelek szerves részei a szövegnek, akkor duplázni kell őket!) Pl.:

Input sor	Output sor
Készítsen #programot#, amely egy $szöveg$ fájl egyes $rész$eit képes …	Készítsen p r o g r a m o t , amely egy szöveg ------ fájl egyes részeit képes ... ----
… a szövegben ##-, illetve $$- jelek közé …	… a szövegben #-, illetve $- jelek közé …

18. Készítsen programot, amely egy szöveg fájlban található tetszőleges fixpontos számot (egészrész . törtrész) átalakít normálalakba (mantissza E karakterisztika), illetve vissza! Lásd az alábbi példát!

Input sor	Output sor
Az Avogadro-szám: 6.0E23 nagyságú szám.	Az Avogadro-szám: 6.0E23 (=600 000 000 000 000 000 000 000.0) nagyságú szám.

19.Készíts programot, amely beolvas egy ragozott igét, majd megmondja, hogy milyen időben, számban, illetve személyben van!

20.Készíts programot, amely beolvas egy egyszerű mondatot (alany, állítmány, esetleg névelő lehet benne), majd egy segédszótár segítségével megadja, mi az alany, illetve az állítmány!

21.Készíts mondat, illetve szöveggeneráló programot! A mondatban alany, állítmány, illetve tárgy lehet, a program a lehetséges szavakat saját szótárából vegye!

22.Készíts programot, amely szöveg egyes részeit képes kiemelni (aláhúzással, ekkor persze a szöveg minden második sorban lesz, s a közbülső sorokba tesszük, ha kell, az aláhúzó _ jeleket). A kiemelendő részeket a szövegben #-jelek közé tettük.

23.Készíts programot, amely egy szövegben hézagos mintát tud keresni! A hézagokat (tetszőleges karakter lehet a helyén) a keresett szóban $-jel jelöli. Pl., ha a keresett szó "ba$$a", akkor a szövegben levő "balra", "balta", "bamba" ... szavak is megoldásai a keresésnek!

24.Készíts programot, amely beolvas egy toldalékokkal ellátott főnevet, s leválasztja belőle a toldalékokat! (Pl. toldalékokat -> toldalék + ok + at.)

25.Készíts programot, amely egy szövegként tárolt oktadecimális számot decimálisra, illetve decimális számot oktálisra alakít!

26.Készíts programot, amely szöveg egyes részeit képes kiemelni (duplázva írni: azaz minden betűjét kétszer írja egymás után, pl. alma ® aallmmaa). A kiemelendő részeket a szövegben #-jelek közé tettük.

27.Matematikai szövegekben gyakran előfordulnak görög betűk (alfa, szumma, … ómega), illetve speciális szimbólumok (kisebb-egyenlő, végtelen, eleme, …). Írjunk konverziós programot, amely képes az alább felsorolt jeleket megfelelőjükkel helyettesíteni! A szöveget egy szöveg file tartalmazza. Idézőjelek közé tett részt átalakítás nélkül kell átmásolni! Megfeleltetés (… kódlapot feltételezve):

Szöveges	Szimbolikus	ASCII-Kód	Szöveges	Szimbolikus	ASCII-Kód
alfa	a	224	végtelen	¥	236
béta	b	225	eleme	Î	238
PI	P	227	metszet	Ç	239
SZIGMA	S	228	azonos	º	240
mű	m	230	Plussz-minusz	±	241
delta	d	235	nagyobb-egyenlő	³	242
ÓMEGA	W	234	kisebb-egyenlő	£	243

A program igény szerinti „irányú” megfeleltetést elvégzi, s az eredményt egy szöveg file-ba írja. Pl.

Input sor	Output sor
… A2S º S(i=1..N) T(X(i)£d)…	… A2S AZONOS SZUMMA(i=1..N) T(X(i) KISEBB-EGYENLŐ DELTA )…

28.Készítsen titkosító, illetve megfejtő programot! A jelek kódja, amelyre építünk egy byte-os (pl. ASCII). A titkosírás módszere legyen a következő (Bináris Vignère):

·Legyen adva egy kulcs-szó (pl. „SzP”), amely jeleinek belső kódja, mint maszkolási érték funkcionál (pl. „SzP” Þ (83=01010011₂, 122=01111010₂, 80= 010100001₂), ha a belső kód az ASCII volt).

·A kódolandó szöveghez illesztjük (természetesen csak képletesen) a kulcsot, s az egyes jeleket XORoljuk a kulcs mellé eső jelének kódjával. (próba)[i]

---

[i] Mivel a kódolás során kijöhetnek olyan speciális karakterek, amelyek speciális jelentéssel bírnak egy TEXT fájlban (pl. fájlvégjel), ezért a dekódolhatóság miatt a fájlt típusos (Byte-os) fájlként kell kezelni.

---

[SzP1] Ennek bizony 3-nál több soros output-megfelelője van.