A feladatok köre…
o Pontok
összekötése zárt, nem-metsző poligonná.
o 3
pont „forgásiránya”.
o Egy
pont adott poligon belső pontja-e?
o Egy
pont adott szakaszra illeszkedik-e?
o 2
szakasz metsző-e? Ha igen, mi a metszéspontjuk?
o Ponthalmaz
konvex burka.
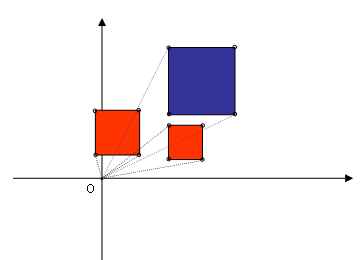
o A(z
origóból) látható négyzetek (pl. megszámlálása).
A fentiek megoldásában szereplő alapvető típusok
(ábrázolás+művelethalmaz): pont, szakasz, pontsorozat.
o
Pont
·
Ábrázolás:
TPont=Rekord(x,y:Valós)
·
Asszociált műveletek szignatúrája:
WritelnTPont(Konst p:TPont)
ReadlnTPont(Vált p:TPont)
ForgásIrány(Konst p,q,r:TPont):{-1,0,+1}
[p®q®r balforgás,
kollineáris, jobbforgású
esetben]
Def-x:
_ ´ _: TPont2 ®R
p1´p2:=p1.x*p2.y-p2.x*p1.y
Megjegyzés:
A
p1´p2 művelet
a ( Æ,p1,p2,p1+p2)
pontok által kijelölt paralelogramma előjeles területét adja.
Tulajdonságai:
|
(T0)
|

|
|
Ha a p az 1. vagy a 4. síknegyedben van, akkor az op-re
illeszkedő egyenes feletti pontokra a p´r>0 alatti pontokra >0.
|
Biz.: p´r=p.x*r.y-r.x*p.y>0 Þ p.x*r.y>r.x*p.y
ha p.x>0, akkor r.y>r.x*p.y/p.x,
azaz r.y>r.x*iránytangens(p)
ha p.x<0, akkor r.y<r.x*p.y/p.x,
azaz r.y<r.x*iránytangens(p)
¨
(T1) p´p=0
Biz.: p´p=
=p.x*p.y-p.x*p.y=0
¨
(T2) p1´p2=-p2´p1
Biz.: p1´p2=p1.x*p2.y-p2.x*p1.y=
=-(-p1.x*p2.y+p2.x*p1.y)=-p2´p1
¨
(T3) (a*p1)´(b*p2)=a*b*(p1´p2)
Biz.: (a*p1)´(b*p2)=(a*p1.x)*(b*p2.y)-(b*p2.x)*(a*p1.y)=
=a*b*(p1.x*p2.y-p2.x*p1.y)=a*b*(p2´p1)
¨
(T4) (p1+q)´p2=p1´p2+q´p2
Biz.: (p1+q)´p2=(p1.x+q.x)*p2.y-p2.x*(p1.y+q.y)=
=p1.x*p2.y+q.x*p2.y-p2.y*p1.y-p2.x*q.y=
=p1´p2+q´p2
¨
(T5) p1´(p2+q)=p1´p2+p2´q
Biz.: p1´(p2+q)=
(T2)Þ =-(p2+q)´p1=
(T3)Þ =-p2´p1-q´p1=
(T2)Þ =p1´p2+p1´q
¨
Megjegyzés:
(T4)&(T5) Þ a ´ disztributív a + műveletre nézve
(T3)&(T4)&(T5) Þ a ´ a vektortéren linearitást tartó leképezés
Def-KSz:
KeresztSzorzat: TPont3 ®R
KeresztSzorzat(p,q,r):=(q-p)´(r-p)=
=(q.y-p.y)*(r.x-p.x)-(r.y-p.y)*(q.x-p.x)
Állítás:
Ha a KeresztSzorzat(p,q,r)>0 , akkor a KeresztSzorzat(p,q,r’)<0,
ahol r’ az r tükörképe a p_q-ra illeszkedő egyenesre
nézve.
Bizonyítás:
(Def-KSz) Þ KeresztSzorzat(p,q,r)=(q-p)´(r-p)
Az világos, hogy
az r a p_q-ra illeszkedő egyenes alatt van Û
ha r-p a 0_q-p-re illeszkedő egyenes alatt
van
(T0) Þ (q-p)´(r-p)>0 Û
ha
r-p a 0_q-p-re illeszkedő egyenes alatt van
No már most az r’ éppen úgy helyezkedik el a
p_q egyeneshez képest,
mint az r’-p a 0_q-p egyeneshez képest: azaz
mindkét esetben a
megfelelő egyenes felett lesz.
(T0) Þ (q-p)´(r’-p)<0 Þ
(q-p)´(r’-p)=KeresztSzorzat(p,q,r’)<0
¨
(maradva csak az első síknegyedben):
1. az r’ a pq-n átmenő egyenes r-hez képesti túl
oldalán lesz.
2a. Tfh. p.x¹q.x Þ
KeresztSzorzat(p,q,r)>0 Þ
(i) r.x¹p.x
(ii) (q.y-p.y)*(r.x-p.x)>(r.y-p.y)*(q.x-p.x)
(i)&(ii)
és a feltevésünk miatt Þ
(q.y-p.y)/(q.x-p.x)>(r.y-p.y)/(r.x-p.x) Þ
iránytangens(p-q)>iránytangens(p-r)
1.Þ iránytangens(p-q)<iránytangens(p-r’)
… visszafelé elvégezve a keresztszorzat-számítást
Þ
KeresztSzorzat(p,q,r’)<0
2b. Tfh. p.x=q.x Þ
KeresztSzorzat(p,q,r)>0 Þ (q.y-p.y)*(r.x-p.x)>0
és
r’.x=p.x-(r.x-p.x)=2*p.x-r.x
továbbá
KeresztSzorzat(p,q,r’)=(q.y-p.y)*(2*p.x-r.x-p.x)=p.x-r.x<0
¨
Az állítás következménye, hogy a ForgásIrány-számítást
alapozni lehet a Kereszt–Szorzat
képletére.
o
Szakasz
·
Ábrázolás:
TSzakasz=Rekord(p,q:TPont)
·
Asszociált műveletek szignatúrája:
WritelnTSzakasz(Konst s:TSzakasz)
Problémamentes.
l. a programban (55.
sor környékén).
ReadlnTSzakasz(Vált
s:TSzakasz)
Problémamentes;
l. a programban (60.
sor környékén).
SzakaszonE(Konst s:TSzakasz; r:TPont):Logikai
Állítás:
p,q,rÎTPont egy egyenesen vannak Û
KeresztSzorzat(p,q,r)=0
Bizonyítás:
(Þ)
p,q,rÎTPont egy egyenesen vannak Þ $lÎR: r=p+l*(q-p) Þ
KeresztSzorzat(p,q,r)=(q-p)´(r-p)=(q-p)´(p+l*(q-p)-p)=
=(q-p)´(l*(q-p))=
(T3) Þ =l*(q-p)´(q-p)=
(T1) Þ =l*(q-p)´(q-p)=0
(Ü)
KeresztSzorzat(p,q,r)=0 Þ
(q.y-p.y)*(r.x-p.x)-(r.y-p.y)*(q.x-p.x)=0
Þ
(q.y-p.y)*(r.x-p.x)=(r.y-p.y)*(q.x-p.x) Þ
1. ha (q.x-p.x)¹0 és (r.x-p.x)¹0 Þ
(q.y-p.y)/(q.x-p.x)=(r.y-p.y)/(r.x-p.x) Þ
Iránytangens(q-r)=Iránytangens(r-p) Þ
p,q,rÎTPont egy
egyenesen vannak.
2. ha (q.x-p.x)=0 Þ
p_q-n átmenő egyenes az
x-tengelyre merőleges és
(r.x-p.x)=0 vagy
(q.y-p.y)=0 Þ
2a.ha (r.x-p.x)=0 Þ
p_r-n átmenő egyenes az x-tengelyre
merőleges Þ
p,q,rÎTPont egy
egyenesen vannak.
2b. ha (q.y-p.y)=0 Þ
p=q Þ
p,q,rÎTPont egy
egyenesen vannak.
¨
Állítás:
ha p,q,rÎTPont egy egyenesen vannak és
r.xÎ[Min(p.x,q.x)..Max(p.x,q.x)],
akkor az r a p_q szakaszon
Bizonyítás:
Nyilvánvaló.
¨
Ezen
állításokból adódik már a függvény algoritmusa. L. hátrébb a 70. sor környékén.
SzakaszPárMetszőE(Konst
s1,s2:TSzakasz):Logikai
Állítás:
A szakaszok metszőség-vizsgálatát a ForgásIrány-vizsgálatra vissza lehet
vezetni.
Bizonyítás:
Az alábbi alapesetek képzelhetők el:
|
Alapesetek:
|

|
a.)
ForgásIrány(s1.p,s1.q,s2.p)=ForgásIrány(s1.p,s1.q,s2.q)
és
ForgásIrány(s2.p,s2.q,s1.p)=ForgásIrány(s2.p,s2.q,s1.q)
b.)
ForgásIrány(s2.p,s2.q,s1.p)=ForgásIrány(s2.p,s2.q,s1.q)
és
ForgásIrány(s1.p,s1.q,s2.p)=-ForgásIrány(s1.p,s1.q,s2.q)
c.)
ForgásIrány(s1.p,s1.q,s2.p)=0 és ForgásIrány(s1.p,s1.q,s2.q)¹0 és
ForgásIrány(s2.p,s2.q,s1.p)=-ForgásIrány(s2.p,s2.q,s1.q)
d.)
ForgásIrány(s2.p,s2.q,s1.p)=-ForgásIrány(s2.p,s2.q,s1.q)
és
ForgásIrány(s2.p,s2.q,s1.p)=-ForgásIrány(s2.p,s2.q,s1.q)
¨
Ezen
állításból adódik már a függvény algoritmusa. L. a programban a 80. sor
környékén!
SzakaszPárMetszéspont(Konst
s1,s2:TSzakasz; Vált r:TPont)
Allítás:
Az s1 s2 szakaszoknak az r metszéspontja, ha
van metszéspontja s1-nek és s2-nek, továbbá
$tiÎ[0..1]: ri=si.p+ti*(si.q-si.p)
(i=1,2), ekkor r:=r1=r2
Bizonyítás:
Tfh. Létezik közös pont.
Az alábbi egyenletek megoldása szolgáltatja a megoldást:
(r1=r2=r)
s1.p+t1*(s1.q-s1.p)=s2.p+t2*(s2.q-s2.p) mind x-, mind y-koordinátára Þ
… ennek megoldása ti-kre, majd (a közös és keresett) r.
¨
Ezen
állításból adódik már a függvény algoritmusa. L. a programban a 101.
sor környékén)!
o
Pontsorozat
·
Ábrázolás:
TPontok=Tömb(1..MaxN:TPont)
·
Asszociált műveletek szignatúrája:
A geometriai típusok egyesített
modulja (SZAKPONT.INC):
(*
A szakasz és pont típusának
megvalósítása.
Export:
Konst
MaxN:Egész
Típus
TPont=Rekord(x,y:Valós)
Eljárás WritelnTPont(Konst p:TPont)
ReadlnTPont(Vált p:TPont)
ForgásIrány(Konst
p,q,r:TPont)
Típus
TPontok=Tömb(1..MaxN:TPont)
Típus
TSzakasz=Rekord(p,q:TPont)
Eljárás WritelnTSzakasz(Konst
s:TSzakasz)
ReadlnTSzakasz(Vált s:TSzakasz)
Függvény SzakaszonE(Konst s:TSzakasz; r:TPont):Logikai
SzakaszPárMetszőE(Konst
s1,s2:TSzakasz):Logikai
Eljárás
SzakaszPárMetszéspont(Konst s1,s2:TSzakasz; Vált r:TPont)
*)
Const
MaxN = 9;
Type
TPont = Record x,y:Real
End;
Procedure
WritelnTPont(Const p:TPont);
Begin
Writeln('
x:',p.x:6:3,' , y:',p.y:6:3);
End;{WritelnTPont}
Function
ReadlnTPont(Var p:TPont):Boolean;
Begin
{$i-}
Write('x-,y-koordináták:');
Readln(p.x,p.y);
{$i+}
ReadlnTPont:=IOResult=0
End;{ReadlnTPont}
Function
ForgasIrany(Const p,q,r:TPont):Integer;
(*
Uf:
p->q->r jobbforgású => ForgasIrany(p,q,r)=+1
p->q->r balforgású =>
ForgasIrany(p,q,r)=-1
p-q-r kollineárisak => ForgasIrany(p,q,r)=0
*)
Var
keresztSzorzat:Real;
Begin
keresztSzorzat:=(q.y-p.y)*(r.x-p.x)-(r.y-p.y)*(q.x-p.x);
If
keresztSzorzat<0
then ForgasIrany:=-1
else if
keresztSzorzat>0
then ForgasIrany:=+1
else ForgasIrany:=0
{EndIf}
End;{ForgasIrany}
Type
TPontok = Array [1..MaxN]
of TPont;
Type
TSzakasz = Record p,q:TPont
End;
Procedure WritelnTSzakasz(Const s:TSzakasz);
Begin
Write('Kezdőpont:
'); WritelnTPont(s.p);
Write('Végpont:
'); WritelnTPont(s.q);
End;{WritelnTSzakasz}
Function ReadlnTSzakasz(Var s:TSzakasz):Boolean;
Begin
Writeln('Adja
meg a kezdő- és végpontot:');
ReadlnTSzakasz:=ReadlnTPont(s.p)
and ReadlnTPont(s.q);
End;{ReadlnTSzakasz}
Function
SzakaszonE(Const s:TSzakasz; Const r:TPont):Boolean;
(*
Uf:
SzakaszonE(s,r)=az s szakaszra illeszkedik-e az r pont
*)
Begin
SzakaszonE:={az s EGYENESére illeszkedik-e}
((r.x-s.p.x)*(s.q.y-s.p.y)=(r.y-s.p.y)*(s.q.x-s.p.x))
and
{az s SZAKASZra illeszkedik-e}
(Min(s.p.x,s.qx)<=r.x) and (r.x<=Max(s.p.x,s.q.x))
End;{Szakaszon}
Function SzakaszParMetszoE(Const s1,s2:TSzakasz):Boolean;
Var
fpq1,fpq2,fqp1,fqp2:Integer{-1,0,+1};
Begin
fpq1:=ForgasIrany(s1.p,s1.q,s2.p);
fpq2:=ForgasIrany(s1.p,s1.q,s2.q);
fqp1:=ForgasIrany(s2.p,s2.q,s1.p);
fqp2:=ForgasIrany(s2.p,s2.q,s1.q);
SzakaszParMetszoE:=(fpq1*fpq2<0)
and (fqp1*fqp2<0)
or
SzakaszonE(s1,s2.p)
or
SzakaszonE(s1,s2.q)
or
SzakaszonE(s2,s1.p)
or
SzakaszonE(s2,s1.q)
End;{SzakaszParMetszoE}
Procedure SzakaszParMetszespont(Const s1,s2:TSzakasz;
Var r:TPont);
(*
Ef:
SzakaszParMetszoE(s1,s2) -- s1, s2 egymást metsző szakaszok
Uf:
r rajta van az s1-n és az s2 is
*)
Var
ax,aax,bx,bbx,
ay,aay,by,bby,
t:Real;
Begin
ax:=s1.p.x;
bx:=s1.q.x-s1.p.x; aax:=s2.p.x; bbx:=s2.q.x-s2.p.x;
ay:=s1.p.y;
by:=s1.q.y-s1.p.y; aay:=s2.p.y; bby:=s2.q.y-s2.p.y;
t:=((ay-aay)*bx+(aax-ax)*by)/(bby*bx-bbx*by);
r.x:=s2.p.x+t*(s2.q.x-s2.p.x);
r.y:=s2.p.y+t*(s2.q.y-s2.p.y);
End;{SzakaszParMetszespont}
A fenti típusok műveleteinek gyakorlásaként adjuk meg két
szakasz metszéspontját, ha van!
Demó. (METSZES.EXE)
Program MetszoSzakaszok; {SzP 05.02.11.}
(*
Geometriai feladat 1.
Feladat: Adott szakaszpár
metszés-vizsgálata.
*)
Uses
Newdelay,Crt22,Crt;
{$i AltRutin.inc}{$i SzakPont.inc}
Const
foCim='Metsző szakaszok';
Var
s1,s2:TSzakasz;
r:TPont;
Begin
UjLap(foCim+' -- beolvasás',0);
Repeat
Writeln('Adja meg az S1 szakaszt!');
Until ReadlnTSzakasz(s1);
Repeat
Writeln('Adja meg az S2 szakaszt!');
Until ReadlnTSzakasz(s2);
UjLap(foCim+' -- feldolgozás',-1);
If SzakaszParMetszoE(s1,s2) then
Begin
Writeln('Van metszéspontjuk, mégpedig:');
SzakaszParMetszespont(s1,s2,r);
WritelnTPont(r);
End
else
Begin
Writeln('Nincs metszéspontjuk.')
End;
BillreVar;
End.
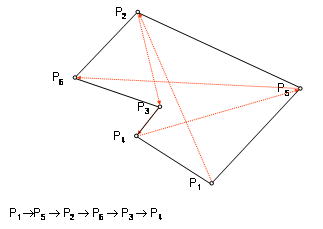
Adott N darab (nem kollineáris) pont. Adjuk meg a pontok
olyan sorrendjét, amelyben az egymást követőket, és az utolsót az elsővel
összekötve zárt, nem-metsző poligont kapunk.
Arra építjük a megoldást, hogy a
ponthalmaz pontjainak egy alkalmas sorrendjét kapjuk, ha a legbaloldalibb-legalsó
pontból „nézve” iránytangensük szerint rendezzük.
|
|

|
|
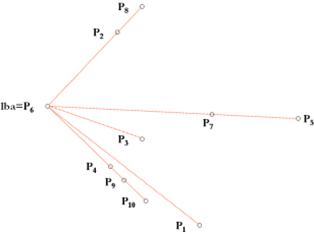
Példa. A ponthalmaz és lba-ból kiinduló és az egyes
pontokban végződő egyenesek.
|
Példa. A pontok és iránytangensük (valamint lba-hoz
való közelségük) szerinti sorrendje,
|
Demó. (PONTSORR.EXE)
Program PontSorrend; {SzP 05.02.11.}
(*
Geometriai feladat 2.
Feladat: adott N (nem kollineáris)
pont. Adjuk meg a pontok
olyan sorrendjét,
amelyben az egymást követőket,
és az utolsót az elsővel összekötve zárt, nem-metsző
poligont kapunk.
*)
Uses
Newdelay,Crt22,Crt;
{$i AltRutin.inc}{$i
SzakPont.inc}
Const
foCim='N ponton nyugvó zárt poligon';
Var
p,pp:TPontok;
s:TSzakasz;
N,i,k:Integer;
Function EgyEgyenesenE(Const N:Integer;
Const p:TPontok):Boolean;
(*
Uf: EgyEgyenesenE(N,p)=BÁRMELY i
ELEME [3..N] :
LÉTEZIK t
ELEME Valós : p[i]=p[1]+t*(p[2]-p[1])
*)
Var
i,j:Integer;
rajtaVan:Boolean;
t:Real;
Begin
{p[j:2..N] pont keresése: p[1].x<>p[j].x}
j:=2;
While (j<=N) and (p[j].x=p[1].x) do
Inc(j);
If j<=N then
Begin {nem mind van a p[1]
"fölött", pl. a j. ilyen}
If j>2 then {garantáltan nem
esnek egy egyenesre, hiszen
a j-1.-ig p[1]-en
átmenő függőlegesre, és
a j. egy
"ferde" egyenesre esik}
Begin
EgyEgyenesenE:=False
End
else {j=2, lehet, hogy egy
"ferde" egyenesre esik mind}
Begin
{p[1]->p[2] iránytangense:}
t:=(p[2].y-p[1].y)/(p[2].x-p[1].x);
rajtaVan:=True;
i:=2;
While (i<N) and rajtaVan {az i. a
p[1]->p[2] egyenesen nyugszik} do
Begin
Inc(i);
rajtaVan:=p[i].y=p[1].y+(p[i].x-p[1].x)*t
End;
EgyEgyenesenE:=rajtaVan
End{If j in}
End
else
Begin {egyetlen függőleges
egyenesen fekszenek}
EgyEgyenesenE:=True
End{If j<=N}
End;{EgyEgyenesenE}
Procedure Poligon(Const N:Integer; Var p:TPontok;
Var pp:TPontok);
(*
Uf: a feladat meghatározása
szerinti sorrendben írja ki a pontokat
*)
Var
i,k:Integer;
Procedure PolarSzogSzerintRendez(Const N:Integer;
Var p:TPontok);
(*
Uf: BÁRMELY i ELEME [1..N-1] :
fi(q,p[i])<fi(q,p[i+1]) ÉS
q ELEME p[1..N] ÉS
BÁRMELY i ELEME [1..N] : q.x<=p[i].x VAGY (q.x=p[i].x => q.y<=p[i].y)
Def: fi: TPont x TPont ->
Valós
fi(q,p):=arctg((p.y-q.y)/(p.x-q.x))
Megj.: az algoritmus működik
az arctg nélkül is, hiszen
rendezéshez fi helyett
tg(fi) is jó, azaz a rendezés a
((p[i].y-q.y)/(p[i].x-q.x))<((p[i+1].y-q.y)/(p[i+1].x-q.x))
alapján is elvégezhető
*)
Type
TIrTg=Record vegtelen:Boolean; irTg:Real End;
Var
i,j,
mini,legbal:Integer;
q:TPont;
plSzog: Array [1..MaxN] of TIrTg;
ir:TIrTg;
Begin
{legbal-alul levő kikeresése:}
legbal:=1;
For i:=2 to N do
Begin
If (p[legbal].x>p[i].x) or
(p[legbal].x=p[i].x) and (p[legbal].y>p[i].y) then legbal:=i
End;{For i}
{polárszög-számítás:}
For
i:=1 to N do
Begin
If
(p[legbal].x=p[i].x) then
Begin
polSzog[i].vegtelen:=True;
polSzog[i].irTg:=0;
End
Else
Begin
polSzog[i].vegtelen:=False;
polSzog[i].irTg:=(p[legbal].y-p[i].y)/(p[legbal].x-p[i].x);
End;{If (p[legbal].x}
End;{For i}
{legbal-alul levőnek az 1. helyre tétele:}
q:=p[legbal]; p[legbal]:=p[1]; p[1]:=q;
ir:=polSzog[legbal];
polSzog[legbal]:=polSzog[1]; polSzog[1]:=ir;
{a többi polárszög szerinti rendezése:}
For
i:=2 to N-1 do
Begin
mini:=i;
For
j:=i+1 to N do
Begin
If
not polSzog[j].vegtelen and
((polSzog[mini].vegtelen) or
(polSzog[mini].irTg>polSzog[j].irTg)) or
((not polSzog[mini].vegtelen) and
(polSzog[mini].irTg=polSzog[j].irTg) and
(p[mini].x>p[j].x))
{p[j]>p[mini]} then mini:=j
End;{For j}
q:=p[i]; p[i]:=p[mini]; p[mini]:=q;
ir:=polSzog[i];
polSzog[i]:=polSzog[mini]; polSzog[mini]:=ir;
End;{For i}
End;{PolarSzogSzerintRendez}
Begin{Poligon}
PolarSzogSzerintRendez(N,p);
{sorrend-korrekció –
az utolsó néhány egy egyenesen
nyugvó sorrendje fordított:}
i:=N-1;
While (p[n].y-p[1].y)*(p[i].x-p[1].x)=
(p[i].y-p[1].y)*(p[n].x-p[1].x) do Dec(i);
Writeln('Az alábbi sorrendben kell a pontokat összekötni:');
db:=0;
{a fordítottak:}
For k:=1 to i do
Begin
WritelnTPont(p[k]); Inc(db);
pp[db]:=p[k];
End;
{a "többiek":}
For
k:=n downto i+1 do
Begin
WritelnTPont(p[k]); Inc(db);
pp[db]:=p[k];
End;
WritelnTPont(p[1]); Inc(db); pp[db]:=p[1];
End;{Poligon}
Begin
UjLap(foCim+' -- beolvasás',0);
Repeat
Writeln('Adja meg a pontok számát!');
{$i-}
Readln(N);
{$i+}
Until (IOResult=0) and (N in [0..MaxN]);
For i:=1 to N do
Begin
Repeat
Writeln('Adja meg a(z) ',i,'. pontot!');
Until ReadlnTPont(p[i]);
End;
UjLap(foCim+' -- feldolgozás',-1);
If EgyEgyenesenE(N,p) then
Begin
Writeln('Egy egyenesen fekszenek. Nincs megoldás.')
End
else
Begin
Poligon(N,p);
End;
BillreVar;
End.
Az oldalt duplavonallal megjelölt kódrész hatékonyabban is
megkonstruálható. Az ötlet:
Az iránytengensek kiszámítása és relációba állítása helyett
egy (matematikailag) ekvivalens és hatékonyan kiszámítható formulán alapuló
relációval helyettesíthető:
{legbal-alul levőnek az 1. helyre tétele:}
q:=p[legbal]; p[legbal]:=p[1]; p[1]:=q;
ir:=polSzog[legbal]; polSzog[legbal]:=polSzog[1]; polSzog[1]:=ir;
{a többi polárszög szerinti rendezése:}
For
i:=2 to N-1 do
Begin
mini:=i;
For
j:=i+1 to N do
Begin
sj:=(p[j].y-p[1].y)*(p[mini].x-p[1].x);
smini:=(p[mini].y-p[1].y)*(p[j].x-p[1].x);
If
(sj<smini) or
((sj=smini) and (p[j].x>p[mini].x)) or
((sj=smini) and (p[j].x=p[mini].x) and
(p[j].y>p[mini].y))
{p[j]>p[mini]} then mini:=j
End;{For j}
q:=p[i]; p[i]:=p[mini]; p[mini]:=q;
End;{For i}
|
|

|
|
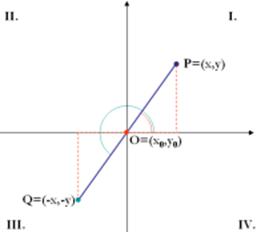
Az iránytangensek nem egyértelműsége.
|
A tangens függvény síknegyedenkénti monoton
növekedése.
|
A pontok egy másik sorrendjét kaphatjuk meg, ha egy „belső
pontból” nézve rendezzük irányszögük szerint. Két kérdést vet föl az ötlet.
1.) mi legyen a belső pont, 2.) az irányszög szerinti rendezést bonyolítja a
tg-függvény p/2-kénti
szakadásai, és a 3.) p-kénti periodikussága, hiszen az 1. és 3. síknegyedbe
„mutató” (p-vel
eltérő) egyenes iránytangense azonos, hasonlóan a 2. és 4. síknegyed esetéhez.
Az 1.) megoldására kínálkozik a ponthalmaz súlypontja, ami
garantáltan belső pont.
A 2.) megoldása (vagy elkerülése) ugyanaz, mint ami volt az
előző megoldás esetében: a p/2 külön kezelése (vagy a tg helyett az ekvivalens
reláció használata); szerencsére a p/2 egész számú többszöröseinél van a síknegyedek határa
is.
A 3.) megoldásának ötlete, hogy a pontokhoz az iránytangens
mellett a síknegyedét is hozzárendeljük: P®(s,t), ahol sÎ[1..4]
– síknegyed, tÎ(-¥,+¥)
– iránytangens; az s meghatározható a P–O koordinátáinak előjeléből (sgn(x-x0),
sgn(y-y0)), a t a P–O koordinátáiból ((y-y0)/(x-x0)).
Így P<Q, ha Ps<Qs, vagy Ps=Qs
és Pt<Qt.
Adott N darab (nem kollineáris) pont. Adjuk meg a pontok konvex
burkát!
Demó. (KONBUROK.EXE)
Az alábbiakban csak a lényegi
eljárás algoritmusát részletezzük:
|
|
|
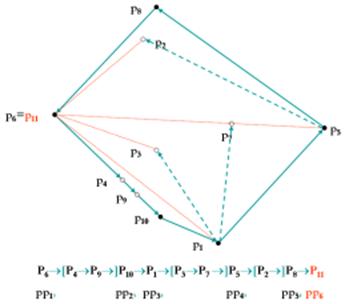
Az algoritmus által követett pontsorrend (a nyilak
jelzik), és ahogy a konvexburokba (pp) bekerülnek az egyes pontok. Szaggatott
nyilak utólag nem helyesnek bizonyuló választásokat jelölnek. A p11 a többletként előre bekerül végpont.
|
Procedure KonvexBurok(Const N:Integer; Var p:TPontok{polárszög-rendezve};
Var
M:Integer; Var pp:TPontok{konvex burok});
(*
Uf: a feladat meghatározása szerinti
sorrendben írja ki a pontokat
*)
Var
i,ii:Integer;
Procedure PolarSzogSzerintRendez(Const N:Integer; Var p:TPontok);
… ugyanaz, mint az előbbi feladatot megoldó programnál …
End;{PolarSzogSzerintRendez}
Begin{KonvexBurok}
PolarSzogSzerintRendez(N,p);
p[N+1]:=p[1];
{az 1. ponttal egy
egyenesre esö pontok átlépése:}
i:=3;
While ForgasIrany(p[1],p[i-1], p[i])=0 do Inc(i);
{ezek közül elegendö az
1. és az "utolsó":}
pp[1]:=p[1];
pp[2]:=p[i-1];
{a többi pont
feldolgozása, hármasával:}
M:=2;
While (i<=N+1) do
Begin
If ForgasIrany(pp[M-1],pp[M],p[i])>=0
{az M. pontnál nem
konvex} then {kihagyható}
Begin
Dec(M)
End
else
Begin {vegyük hozzá az újat}
Inc(M);
pp[M]:=p[i];
Inc(i);
End;{If ForgasIrany}
End;
Dec(M);
{a burok pontjai:}
For i:=1 to M do
Begin
WritelnTPont(pp[i]);
End; {For i}
End;{KonvexBurok}
A feladatok megoldásának főprogramjai (a Turbo Pascal néhány
specialitását kihasználva):
o Szakaszmetszést
vizsgálatának forrása: Metszes.pas;
o Poligont
készítő forrása: Pontsorr.pas;
o Konvex
burok forrása: Konburok.pas.
A feladatokhoz felhasznált „modulok” (unit-ok,
include-állományok):
o A
klaviatúra/fájl-inputhoz: Crt22.pas;
o Általános
rutinok: Altrutin.inc;
o A
grafikus megjelenítés rutinjai: Geograf.inc;
o A
pont és a szakasz típusát leírása: Szakpont.inc.
Adatfájlok (*.dat):
o Metszesa.dat, Metszesb.dat, Metszesc.dat;
o
Pontok0.dat, Pontok1.dat, Pontok5a.dat, Pontok5b.dat, Pontok5c.dat, Pontok6a.dat, Pontok6b.dat, Pontok6c.dat, Pontok8.dat, Pontok9.dat.
Minden együtt: Geometria.zip.