Ebben a leckében informatika módszertani kérdéseket feszegetünk. E kérdésfeltevések a programozás-oktatáshoz kapcsolódnak: milyen gondolkodási műveleteket hajtanak végre a programozás közben a programozók, amelyek azért érdekesek, mert ezek tudatos oktatása fontos lehet (hogy fontos-e, ezt is vizsgáljuk) egyes gondolkodási képességeink fejlesztésében. Illetve sarkalatos kérdésként vetődik föl az első programozási nyelv szerepe.
E fejezetben az [SzP1] irodalomból szemelvényezünk. Elsősorban a Neumann-elvű – más szóhasználat szerint: az algoritmikus vagy imperatív – nyelveken történő programfejlesztésről lesz szó, tehát arról, amely gondolati hátteréül egy ún. Neumann-elvű számítógép szolgál (processzorral, címezhető memóriával, I/O-egységgel). Csak az egy modulból álló programtermékek készítésének didaktikáját vizsgáljuk.
Az itt fölvetett módszertani kérdések, válaszok és fogalmak átszövik a teljes programkészítési folyamatot, tehát éppúgy jellemzik a „nagy”, többmodulos, sőt a nem Neumann-elvű nyelvekre alapozott programozást is.
Fontos előre kiemelni, hogy e fejezet didaktikai kérdéseivel és válaszaival a kezdők, a közoktatásban résztvevő diákok programozásáról gondolkodunk, habár felvetődő egyik-másik probléma átvezet a felsőoktatás, kifejezetten informatikával kapcsolatos (elsősorban informatika tanári) szakok programozás-szerű tárgyainak módszertanába.
Nem tartozik a programozás oktatás első számú mondanivalói közé annak kimondása, hogy abból: „a program termék” az következik, hogy számos olyan lépés tartozik a programkészítés folyamatához, amelyek szükséges adalékként illeszkednek a fő tevékenységek közé. Ennek felvillantására azért mégis célszerű vállalkoznunk az alábbi, így a tanulók számára könnyen felfogható, „pólyai” kérdéseken alapuló megközelítéssel:
| Programkészítési folyamat lépése | Mire keresi a választ | Mi a végterméke? | |
|---|---|---|---|
| Feladatmegfogalmazás | Miből? Mit? Mi a kapcsolat? | Specifikáció |  |
| Tervezés | Hogyan ábrázoljam? Hogyan végezzem el? | Adatleírás + algoritmus | |
| Kódolás | A számítógép hogyan ábrázolja, és hogyan végezze el? | Kód | |
| Tesztelés | Helyes-e? | Tesztesetek |  |
| Hibakeresés | Hol a hiba? | Hibahely-lista | |
| Hibajavítás | Mi a hiba oka, hogyan küszöbölhető ki? | Hiba-ok és javítási javaslat | |
| Hatékonysági tesztelés | Hogyan függ a paraméterektől az időbeli működése és a helyfoglalása? Kielégítő-e? | Hatékonysági tesztesetek |  |
| Rossz hatékonyságú pontok keresése | Mely kódrész felelős a nem várt idő- / helyfelhasználásért? | Problematikus helyek listája | |
| Hatékonyságnövelés | Hogyan gyorsítható, hogyan tehető kisebb helyigényűvé? | Probléma-ok és módosítási javaslat | |
| Dokumentálás | Hogyan telepíthető, használható, hangolható? | Dokumentáció |  |
A „pólyai” jelzőről: Pólya György előszeretettel alkalmazta a matematikai gondolkodás bemutatásánál a kérdéseket. [PGy1] Vallotta, hogy a legrövidebb módja valami kézzel foghatóvá tételének: a kérdéseken keresztüli. Alighanem ő is kijelenthette (volna): a megértés első stációja a kérdezni tudás; amíg valaki kérdezni sem tud, addig semmit sem tud a dologról.
Szó sincs a résztevékenységek végrehajtásának ábra sugallta „egyirányúságáról”. E madártávlatú folyamatleírás tartalmaz természetes ismétlődéseket: „Tesztelés–Hibakeresés–Hibajavítás–Kódolás/Tervezés...”. A fenti táblázat nem törődik a programtermék esetleges „utóéletével”, amelyről a „Karbantartás” lépésben lehetne szólni. Az egyes lépések gyakorlatban összefonódnak. A lépések elvi különválasztásnak csak didaktikai oka van, nevezetesen hogy sajátos módszerek kapcsolhatók hozzájuk, s így könnyebb a „vegytiszta” tárgyalásuk. Ilyen didaktikai szempontok miatt válik külön, pl. a „Tesztelés” és a „Hibakeresés”, bár a programkészítés e fázisában előrehaladva, gyakorta maga a hibakeresés „partikuláris” célja határozza meg a teszteset választását.
Ez a fogalmi tisztázás 0. szintje alkalmas arra, hogy a programozással ismerkedő tudatosabban fogjon bele egy-egy számára célként kitűzött részfeladat megoldásába. Ez annak az általában is működő pedagógiai „madártávlatból közelítés” elvnek alkalmazása, miszerint: a konkrétan vizsgálandó tananyag tágabb témákkal való összefüggéseire hasznos rávilágítani. A tágabb témacsoport kontextusába helyezve válnak érthetővé a taglalt téma céljai, kiindulópontjai. A (majdan tárgyalt) részletek nem lógnak „légüres térben”.
Tapasztalatunk szerint ez a kitekintés kétszer, két helyen is indokolt: egyrészt a téma bevezetőjében, másrészt visszatekintésként az összefoglalásban. E „keretbe foglalás” elvet is egy, általában alkalmazható alapelvnek tekinthetjük.
Előbb a lényegibb lépcsőkön (a programozáshoz közvetlenebbül kapcsolódókon: feladatmegfogalmazás, tervezés és kódolás) tanítsuk meg járni a tanulókat, majd később persze foglalkozni kell a „kevésbé fantáziamozgató” lépésekkel is. Akkurátusan megkülönböztetjük a programkészítési folyamatot a programozási folyamattól. Az előbbinek az utóbbi csak része, a legkreatívabb részfolyamata.
Miközben a programozó a feladat megoldásán fáradozik, tudatosan vagy sem, számos gondolkodási módszert használ. Ahogy a feladatból kiindul, többszörösen szelídíti azt a saját, meglévő, tapasztalatain alapuló sémáihoz, körkörösen haladva egyre pontosabban fogalmazza újra a feladatot. Úgy is mondhatjuk, hogy a programozás a feladat egyre finomabb (sémákon alapuló) modelljeinek sorozata, amiben addig kell eljutni, ahol már a választott programozási nyelv szókincse (utasítás-sémáinak halmaza) jelenti a modell alapját.
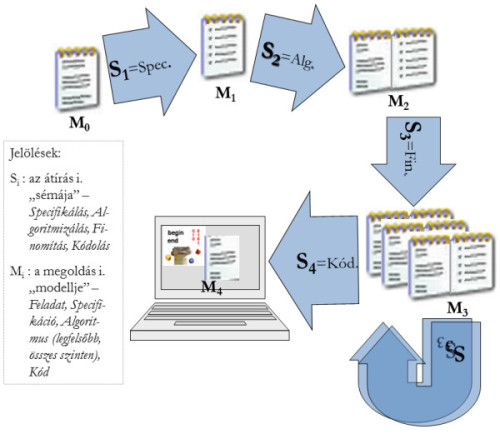A programozás absztrakt modelljeA programozó legfontosabb gondolkodási műveletei a finomodó modellek felállításánál:
Az egyes eszközöket sokszor, sokféle céllal veti be a programozó. Ez indokolja, hogy kénytelen leszek ugyanazt az eszközt többször is szóba hozni.
Ez a gondolkodási eszköz 3 ponton nyugszik. 1) egy nyelv elsajátítása nagyfokú absztrakciót kíván, hisz minden nyelv elemei (szavai), struktúrái (szabályai által megszerkesztett nagyobb egységek, pl. képzett, ragozott szavak, mondatok) elvonatkoztatások. Ezek szintaktikus és szemantikus viszonyainak ismerete nélkül reménytelen bármely nyelv helyes alkalmazása. Amint láttuk 2) a programozás modellsorozat-gyártás (a feladattól a kódig); s 3) Az egyes modellekhez sajátos szókincs és leírási szabályok tartoznak.
Világosan látnunk kell, hogy a szintaxisnak két szintje van: a „konkrét” szint az „írásos” szint (erre vonatkoznak a nyelv helyesírási szabályai), az absztrakt szint mentes a leírás „akkurátusságától”, csak a lényegi vonásokat tartalmazza (lehetnek benne hibás „szavak”, hibás „szószerkezetek”, ha egyértelműen dekódolható, akkor ugyanolyan jó, mint az azonos értelmű hibátlan).
A modell-nyelvek 3 fajtáját vizsgáljuk: 1) a feladatmegfogalmazás (v. specifikáció), 2) a tervezés (v. algoritmizálás), 3) kódolás.
Az első absztrakciót maga a feladatmegfogalmazás kívánja. A feladatmegfogalmazás során először is a feladat szempontjából lényeges és a lényegtelen dolgok leválasztása zajlik. Az informálisan megfogalmazott feladatszövegből kihámozandó lényeges mondanivalók a következők: mik a kiinduló adatok, melyek a megoldás során meghatározandók; milyen feltételeket lehet figyelembe venni a kiinduló adatok között, és hogyan függnek az eredményadatok a kiindulóktól. Hasonló a tanuló dolga, mint a matematikai szöveges feladatoknál: értelmeznie kell tudni. A fent felsoroltak adnak támpontokat az értelmezéshez.
A specifikációs nyelv szókincsét, szerkezetét ezek alapján hozzuk létre. Az absztrakt szintaxis megtervezése történhet „pólyai alapokon”:
Ezt követi az adatok jellemző attribútumainak konkrétumoktól elvonatkoztatása: a tipizálás, azaz a konkrét adatok értékhalmazzá általánosítása, majd ennek az adatokhoz rendelése. Itt néhány alaphalmaz közül egy – vagy összetett adat esetén: több – megfelelőt választunk ki, majd – szükség szerint – megengedett halmazműveletek felhasználásával hozzuk létre az összetett adat alaphalmazát.
Ezt a lépést azért soroltuk a nyelvi absztrakciós lépések közé, mert a programozónak még formalizált eszközök alkalmazása nélkül is, intuitíve tisztában kell lennie azzal a „nyelvi kerettel”, amelyben gondolkodnia kell az adatokról. E nyelvi keret minimálisan a következőket jelenti: a halmaz fogalma, a kiindulásul választható halmazok készlete és konstrukciója. E nyelv Chomsky értelemben véve nyelvnek tekinthető, amely igen egyszerű grammatikával írható le.
... nyelvnek tekintem a mondatok valamely (véges vagy végtelen) halmazát; minden egyes mondat véges hosszúságú, és elemek véges halmazából épül fel. ... valamely formalizált matematikai rendszer „mondatai” is nyelvnek tekinthetők. [CN/15.o.]
Csak „hiedelem”, hogy lehet programozni specifikálás nélkül! Minden programozó specifikál, csak éppen tudat alatt, illetve ezt a tevékenységet a következő lépéssel (rosszabb esetben a kódolással) együtt végzi ... s ebből támadnak a gondok. E nyelv „szintaktikájának” ismerete csupán annyira feltétele a nyelv ismeretének, amennyire egy természetes nyelv esetében az írás (a „formális” nyelvtan) ismerete (vö. specifikációs analfabetizmus).
A következő nyelvi absztrakciót igénylő helyzetbe a tervezés során kerül a programozó. Ekkor a tervezéshez választott leíróeszköz ismerete igényli a nyelvi absztrakciós készséget. A tervezés valamely „szabványos” leírónyelven történik. Például:
Ezek közül az első kettő „rajzos” nyelv, a harmadik hagyományos szöveges nyelv.
Úgy az adatleírásban, mint az algoritmizálásban föl kell ismerni a jellegzetes és elegendő struktúrákat, amelyekhez célszerű egyértelmű, de kellően rugalmas nyelvet kidolgozni.
Mit is jelentenek a jelzők:
Számos ilyen nyelvet dolgoztak ki az idők során. Több szempont figyelembe vételével alakítottuk ki azt a magyar nyelvű pszeudokódos formalizmust, amellyel az algoritmusainkat készítjük.
Érdemes látnunk, hogy a tervezés során több féle szinten is alkalmazza a nyelvi absztrakciót a programozó. A legalsóbb szint: az ún. utasítás szint, ennél a nyelv szavai az algoritmikus nyelv utasításai, a nyelv struktúráit maga az algoritmikus nyelv definiálja (az ő szintaxisával). Szokás ehhez a szinthez venni a finomításokat is. Ekkor persze a nyelv szókincse dinamikusan bővül a finomítások neveivel, a struktúrákhoz hozzá kell venni a finomítások definiálásának szintaxisát, valamint a finomítás használatét. A következő szint a programozási nyelvek szintje. E szint az előző bővítése. Ide kerülnek a tételek definiálásának és alkalmazásának szintaxisa (ami célszerűen alig tér el a finomításokétól). A szintemelkedést a tételek szemantikájának magasabb foka okozza. Világos, a tételek előre definiáltan kerülnek a nyelvbe bele (azaz éppúgy kötöttek, mint az algoritmikus nyelv utasítás-elemei). A nyelv bonyolódása tehát elenyésző, míg az algoritmikus, absztrakciós tartalomé jelentős. A harmadik nyelvi szint a modularizációs szint. Ez is bővíti az előző szintet, jelesül a modul fogalom bevezetésével mind a definíciós, mind az alkalmazás szintaxisával. Úgy is fogalmazhatunk: ez a „szerszámkészítés” szintje. Az ezen a nyelven „beszélőnek” azt kell jól látnia, hogy a „szerszám” (pl. egy frissen létrehozandó típus) miként lesz kényelmesen, hatékonyan, emellett biztonságosan felhasználható a mindenkori programozó számára. Megint másként fogalmazva: az „eszköz-funkció-univerzum” gyártás szintje, amelynek során a mindenkori programozó elvonatkoztatására épít a modell-programozó.
Egy kis kitérő a „rajzos algoritmikus nyelvhez”:
Itt említjük meg azokat a grafikus „praktikákat”, grafikus nyelvi megoldásokat, amelyekkel a programozó tevékenysége során sokszor él. Nem az algoritmuskészítéshez kitalált számos „rajzos” eszközre, úgymint blokk diagramra, struktogramra vagy Jackson-féle diagramra gondolunk, hanem azon ábrákra, „margószéli firkákat”, amelyekkel a programozó megpróbálja az algoritmus lényegét elkapni, vagy az adatokat a memóriába képezni. (Egy kellően összetett, láncolt szerkezet esetén szinte „kötelező” ilyen rajzokat készíteni, hogy rajta követni lehessen az egyes algoritmusdarabkák működését.) De még egyszerűbb feladatok esetén is, annak jobb megértéséhez gyakorta készül grafikus vázlat; mondhatjuk így: a probléma „statikus vizualizációja”. Például a beillesztéses rendezést lényegét, lépéseit az alábbi ábrapár jól demonstrálja.
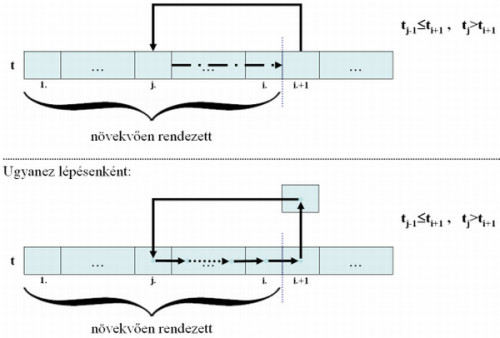A beillesztéses rendezés algoritmusának „statikus vizualizációja”Pólya György következő gondolatai könnyen adaptálhatók a megfelelő ábra megtalálásának programozásbeli problémájára [PGy1/71. o.]:
Az ilyen típusú feladat beható elemzését azzal kezdjük, hogy felrajzolunk egy olyan ábrát, amely tartalmazza az ismeretlent és az adatokat, mégpedig olyan elrendezésben, ahogy azt a feladat kikötése előírja. Ahhoz, hogy a feladatot világosan megértsük, minden adatot, a kikötés minden egyes részét külön-külön szemügyre kell vennünk; akkor azután egyetlen képbe egyesítjük az összes részleteket, a kikötést mint egészet vizsgáljuk meg, és megpróbáljuk együtt látni a feladat által előírt különféle összefüggéseket. Mindezeket a részleteket papirosra felrajzolt ábra nélkül aligha tudnánk kézben tartani, szétválasztani és ismét összerakni.
Összegezve a fentieket: a tervezés során a programozó a szabványos algoritmus leíró nyelvek mellett nem „szabályozott szintaxisú” nyelvet (a grafikus „kapaszkodókhoz”) is alkalmaz.
A harmadik nyelvi kihívás maga a kódolás. Itt komoly absztrakcióra már kevés szükség van akkor, ha a programozó eljut arra a felismerésre, hogy egy jól végiggondolt algoritmus után az adott konkrét programozási nyelvre való átültetés, azaz a kódolás nagyrészt mechanikusan elvégezhető. Annyira jelent nyelvi absztrakciós tevékenységet, amennyire egy primitív szintaxisú nyelvpár közötti fordítói tevékenység.
Ennek feltétele, hogy ki legyenek dolgozva azok a kódolási szabályok, amelyek többé-kevésbé egyértelmű kapcsolatot létesítenek az algoritmus nyelvi elemei és a programozási nyelv struktúrái között. A „többé-kevésbé” jelzi, hogy mindenképpen jelen van az absztrakció, legfeljebb a foka jellemzi a programozó gyakorlottságát, tudatosságát.
Analógiák szerint gondolkodni, nincs ebben semmi kivetendő:
az analógia előnye,
hogy nem zár le semmit és tulajdonképp nem követel semmi végsőt;
árt viszont az oly indukció, amely eleve kitűzött célt követ,
s erre törve hamisat-igazat egyképp ragad magával.
[Goethe]
Ez a legtermészetesebben – mondhatjuk: – ösztönösen alkalmazott gondolkodási művelet. Lényege: amikor a programozó egy jól definiált (rész)feladat megoldását keresi, először is memóriájában valamilyen „rokonfeladat” után kutat, amelyből kiindulhatna. Ilyenre bukkanva, felidézi annak „bevált” megoldását, majd „kitapogatja” a megoldandó és a mintául szolgáló feladat kapcsolódási pontjait, hogy ezeket egymásnak megfeleltetve alkalmazza a már ismert megoldást. Tehát az analógiás feladatmegoldás sémája:
Vegyük észre, hogy az analógiás gondolkozás alapja (is) az elvonatkoztatás. Például a feladat paramétereinek felismerése a lényeg és a lényegtelen, a lényeg (az absztrakt) és a konkrét megkülönböztetése.
Két kérdés vetődik föl a fenti sémával kapcsolatban. Egyrészt: „Mi az, hogy rokonfeladat?” Másrészt: „Miben rokon két megoldás?”
Rokonfeladatok, amelyekben azonos a problémafeltevés módja függetlenül az adatok esetleg eltérő konkrétumaitól (pl. az adatok típusától). A rokonfeladatokban azonos szerepet töltenek be az adatok, azonosak a kapcsolataik. Hogy egy programozó milyen feladatokkal találkozik, az esetleges. Így a feladat- és megoldásbázis is lehet egyénenként különböző. Mégis összeállíthatók olyan tipikus problémafeltevések, amelyekkel tapasztalat szerint a feladatok legalább 90%-ához meg lehet találni az analogont (esetleg többet is):
Az „azonos problémafelvetés”-t jelezheti (Pólya után) a kérdőszó. De figyeljünk rá, mert csalóka lehet! Például: „Melyik?” (kiválasztás) = „Hányadik?” (kiválasztás) ≠ „Melyik?” (maximum kiválasztás) Ugye mennyire másról van szó!
Ezeket a sémafeladatokat az autodidakta programozó is előbb-utóbb felismeri sok-sok feladat megoldása után. Nagyban siettethető azonban a felismerési folyamat, ha e sémákra a programozási alapszókincs megismerése és némi gyakorlása után nem sokkal módszeresen rávezetjük a tanulókat. Történhet ez néhány, célzottan összeválogatott, konkrét feladat elemzésével, majd ezekből levont tapasztalatok általánosításával (csak a lényeget tekintve, formalizmusmentesen: [SzPZsL2]), illetve definitíve, formálisan [FÁ]. Az előbbi módszer elsősorban középszintű oktatásban alkalmazható, míg a második kellő formális matematikai ismeretek birtokában levő egyetemisták esetében.
Nem érdektelen itt idézni Pólya Györgyöt az általa „származtatási elv”-nek nevezett elvről [PGy2/II. kötet 143.o.]:
... A származtatási elv szerint a tanulónak azt az utat kell követnie, amelyiken az igazi feltalálók járnak. A tanulónak – az aktív tanulás elve szerint – annyit kell felfedeznie az anyagból, amennyit csak képes. A két elv összekapcsolása mutat arra, hogy a tanulónak újból kell felfedeznie azt, amit meg kell tanulnia.
Vagyis a pólyai származtatási elvet igazítottuk a programozáshoz, amikor a programozó-felfedezők szisztematikusságával válogattuk össze a felfedezendő sémafeladathoz elvezető konkrét feladatokat.
Fontos észrevennünk, hogy az analóg sémák szisztematikus bevezetése a bevezető fejezetben érintett szűkös oktatási időkeret miatt feltétlenül indokolt. Komoly pedagógiai probléma azonban megtalálni az „irányított” és saját „aha-élményeken” alapuló megközelítés megfelelő aránya. Szélsőségek között kell a korcsoport számára megtalálni az ideális arányt: a teljesen, önálló felfedezéseken alapuló és a kicsiszolt, preparált sémákon alapuló megközelítés között.
Az irányított mellett szól a kevesebb időigény, a saját élményeken alapuló mellett a közismert mélyebb rögzülés. Az előbbi tekinthető akár lexikális megközelítésnek (rossz megvalósítás esetén valóban az is), míg a második kreativitást fejlesztőnek. Tehát az idő szűke és a kreativitás fejlődése áll antagonisztikusan szemben egymással.
Rokonmegoldás: szerkezetileg azonos algoritmus. A szükséges szerkezeti elemek a strukturált programozás által bevezetett elemi utasítások és utasításkonstrukciós eszközök. (Vö. nyelvi absztrakcióval.) Az utasításkonstrukciók:
Elemi utasítások:
A (d) és az (f) – adott esetben az (e) – a „felülről lefelé tervezés” közismert programozási elvének követése az algoritmikus nyelvben. (Lásd a „Dekompozíció, szuperpozíció” alfejezetben!)
Érdekes, hogy a kezdő programozók (nyugodtan mondható, hogy kódolók) az analógiák felismerésére többnyire éppen a kódhasonlóság észrevételével jutnak el.
A programozás során sokszor és sokféle fokon használja a programozó az általánosítás gondolkodási eszközt. Ennek egyikét már az analógiákkal foglalkozó részben a feladatsémákkal kapcsolatban érintettem. Kiderült, hogy az analógiás gondolkodást hatékonyabbá lehet tenni bizonyos, jól megválasztott sémák kidolgozásával és oktatásbeli bevezetésével. Mivel a sémák absztrahálás útján jönnek létre, ebből a szempontból is meg kell vizsgálnunk!
A kiinduló analógiakészletet memóriakímélő módon úgy készíthetjük el, ha számos konkrét rokonfeladatot (és megoldását) általánosítjuk: elkészítjük absztrakciójukat. Azaz a rokonságot kidomborítjuk, az egyedi különbözőségeket elimináljuk az egy „közös ős” megtalálása kedvéért.
Vegyük észre ezzel a PISA-i kritika egyikére: a túlzásba vitt lexikalizált oktatásra kínálunk most egyfajta gyógymódot.
Az analógiabázisnak egy-egy eleme: egy absztrakt feladat és egy hozzá illeszkedő, legcélszerűbbnek talált megoldás. E gondolat vezet el a programozási tételek fogalmához: absztrakt feladat + absztrakt algoritmus + helyességbizonyítás. A bizonyítást természetesen nem kell állandóan észben tartani, elegendő csak egyszer elvégezni (az oktatás során akár egyszer sem!). Pontosan úgy, ahogy a természettudós tesz kutatása során az alkalmazott tételekkel: ellenőrzi a feltételeket, és mondanivalójának célirányosságát, majd elfogadja helyességét vizsgálat nélkül, hogy azután felhasználja. A következő táblázatban egy példát adunk programozási tétel definiálására a „Nyelvi absztrakciók” alfejezetben tárgyalt két (a specifikációs és az algoritmikus) nyelv felhasználásával.
A programozási tétel része | Példa |
|---|---|
Absztrakt feladat – specifikáció: | Eldöntés(H*,F(H,L)):L Bemenet: N∈N, X∈H*, T:H→L Kimenet: VAN∈L Előfeltétel: N=Hossz(X) Utófeltétel: VAN = i∈ [1..N] : T(xi) |
Absztrakt megoldás: | Konstans MaxN:Egész(???) Eljárás Eldöntés(Konstans N:Egész, X:THk, |
Bizonyítás: | Ezt most hosszadalmassága miatt elhagyjuk. |
Néhány megjegyzés a táblázathoz:
A programozási tételek jól ismertek a programozás módszertanban. Sajátos formalizmussal [SzPZsL1/41-54] definiálva a 17 legfontosabbat (és néhány speciális változatát) megtalálhatjuk a következő irodalmakban: [SzP3, SzPZsL1]. A feladatleíró nyelv – amint a korábbi példából kiderült – halmazelmélet és elsőrendű predikátumkalkulus elemein alapulnak. Középpontjában a sorozat matematikai fogalma áll. Számos más nyelvet is megalkottak a specifikációkészítéshez. Például egy, a sorozatok helyett halmazokon nyugvót alkalmaznak az [FÁ] irodalomban. Didaktikai okok miatt döntöttünk a sorozat központi szerepe mellett: mivel a sorozat fogalma közelebb áll a kezdő programozók által előszeretettel használt algoritmikus tömb fogalmához, ezért helyeztük e fogalmat a leírásunk fő helyére. A tervezés nyelve egy magyar kulcsszavakon alapuló pszeudokód.
A programozási tételek alkalmazásakor a programozó egyrészt absztrahál: elnevezi és körülírja a részfeladatot jelentő finomítást, majd egy tételanalógiát keres, amely ráhúzható a körvonalazott részproblémára. A programozási „hétköznapokban” sokszor a tételeknél „elemibb” absztrakciókat használ a programozó. Nézzük, mik ezek!
Akkor, amikor a felülről lefelé tervezés stratégiai elvet alkalmazza a programozó, s ezt tükrözi az algoritmikus nyelv egy újonnan bevezetett eljárásával vagy függvényével (finomítás), lényegében a nyelvet, magát bővíti az új fogalommal (vö. a nyelvi absztrakcióval). A nyelv szókincséhez egy elem hozzávétele két dolgot jelent. Egyrészt a fogalom „alakjának” (szintaxisának) és elvárásának összekapcsolását (ez az absztrakció), továbbá a mögöttes tartalom, a szemantika definiálását jelenti (az pedig a specializáció). A programozásban ezt a fajta építkezést nevezik algoritmikus absztrakciónak, tehát némileg szűkebben értelmezik nálunk. Ez az építkezés azonban – többnyire – sok lépésben halad előre, mondják úgy is: a megoldást lépésenként finomítva, a programozási nyelvhez közeli szintig kell folytatni. Így hozunk létre a feladathoz illeszkedő (absztrakt) fogalomhierarchiát.
Tapasztalat szerint a fogalom megismerése két szinten zajlik: az első szinten a kezdő programozó megérti, hogy ezzel egyrészt egy algoritmusrövidítő eszköz birtokába jut, másrészt ennek alkalmazása során fogalmazódik meg benne a paraméterezhetőség igénye. Érdekes, hogy az algoritmusrövidítés, egyébként másodlagos előnyét hamarabb konstatálják mint a fő értékét: a szellemi energiájuk optimálisabb beosztását lehetővé tevő „oszd meg és uralkodj” elv kivitelezhetőségét. A paraméteres finomítás fogalmában további nehézséget a formális és az aktuális paraméterek elválasztása, és helyes értelmezése jelenti. Ezért írtam a megértés két szintjéről, amelynek 2. szintjét jelenti a paraméterek okozta absztrakciós gát átugrása.
Még egy, absztrakcióval összefüggő algoritmikus gondolatot említek. A „feladat általánosítása” módszertani elvünk [SzPZsL1/97] betartása is egy absztrakciós lépés jelent a tervezésben. Lényege: nemcsak a konkrét feladatra, hanem egy bővebb feladatkörre alkalmazható programot érdemes alkotni úgy, hogy a feladatban szereplő fogalmakat (elsősorban konstansokat) általánosítjuk.
Legegyszerűbb esetben a feladatbeli konstansokat szimbólumokkal helyettesítve építjük be a megoldásba. A szimbolikus adatok válhatnak a feladat eredeti megfogalmazásához képest többlet bemenő paraméterekké, de lehetnek csak szimbolikus konstansok (belső paraméterek). Már ez utóbbi esetben is számolhatunk azzal az előnnyel, hogy e konstans értékét érintő karbantartási változtatásokat egyetlen mozdulattal és teljes biztonsággal hajthatjuk végre.
Például a „soroljuk fel egy kosárlabda-csapat játékosai közül a 210 cm-nél magasabb játékosokat” feladatban, kézenfekvő általánosítás lehet
Ehhez hasonlóan járhatunk el a feladat „indukálta” típusokkal is. Azaz ahol lehet, általánosabb alaphalmazokkal dolgozzon a majdani program. Természetesen az általánosítás itt jól kitapintható hatékonysági kérdéseket is fölvethet. Például a fenti feladat esetében a következő típusokat érintő általánosításokra gondolhatunk:
A feladat most elemzett általánosítása tehát nem annyira absztrakciós nehézségeket okoz a programírónak, sokkal inkább az ideális arány megtalálása a feladatszintű általánosság és a tervezés szintű hatékonyság között okozhat fejtörést.
Ezt a fajta feladat-absztrakciót ötvözhetjük a finomításossal. Nézzük a fentebb említett feladatot! Az algoritmusbeli magassági korlátra vonatkozó reláció helyett egy általánosított tulajdonságot megtestesítő (azt általánosító) logikai függvény is szerepelhet. Ez által megoldásunk minden olyan feladatnak majdnem kész megoldása lesz, amelyben „csak” a játékos érintett tulajdonsága változik az itt említetthez képest.
Visszatekintésül az általánosítás következő területeit érintettük ebben az alfejezetben:
Az algoritmikus absztrakción keresztül felismerhetjük a gondolati absztrahálódás általános működését. [FI/18. o.] nyomán:
Ugyanezt követhetjük nyomon az adatok fogalmának metamorfózisán az [SzPZsL3] alapján.
A dekomponálás a komplex probléma elemibb problémák együttesére bontását jelenti. Az elemi illetve komplex probléma viszonyát megfordítva sokszor szuperponálásról beszélnek: ekkor a komplex probléma elemi feladatokból való felépítésére gondolnak. A lényeg ugyanaz: a komplex probléma és elemibbek kapcsolatba hozása.
Az emberi elme jól ismert pszichológiai korlátjáról így ír – szabadon idézve – Mérő László: az emberi agy rövid távú memóriában egy időben tartható a sémák, azaz gondolkodási struktúrák maximális száma egyénenként a 7±2 érték körül mozog. [ML/12. o.] Ez egyszerűen szólva azt jelenti, hogy az ember tervezéskor pl. nem igen képes áttekinteni olyan „bonyolultságú” tervet, amelynek sémaszáma a fenti értéket meghaladja. Ezek szerint a strukturált programozás már többször emlegetett felülről lefelé tervezés, vagy hétköznapi szavakkal mondva: az „oszd meg és uralkodj” elve pontosan ezen emberi gyengeség beismerését, sőt elkerülésének módját fogalmazza meg, számszerűsítés nélkül. Tehát egy, programozásból kihagyhatatlan elvről van szó.
E gondolkodási művelet lényege, hogy a feladatot egyre finomodó műveletkészlet segítségével fogalmazzuk meg újra meg újra, amíg az algoritmikus nyelvünk eleve meglévő utasításáig el nem jutunk. Minden szint a feladatot teljesen megoldja, de a szint egy-egy összetett sémája (eddigi szóhasználatunk szerint: finomítása) csak kb. 5-9 még elemibb mikro sémára (azaz finomításra, vagy már definiált műveletre) bomlik.
Cormen és szerzőtársai [CTLCRR/10. o.] könyvükben így közelítik meg a lényeget:
„Az oszd meg és uralkodj paradigma a rekurzió minden szintjén három lépést vesz igénybe:
Felosztja a problémát több alproblémára.
Uralkodik az alproblémákon rekurzív módon való megoldásukkal. Ha az alproblémák mérete kicsi, akkor közvetlenül oldja meg az alproblémát.
Összevonja az alproblémák megoldásait az eredeti probléma megoldásává.”
Ehhez érdemes következő észrevételt hozzátenni:
Az alproblémák (vagy a pszichológia szerint: sémák) összevonása a megfelelő utasítás-szervezés kiválasztását jelenti. El kell rendezni az alproblémákat a rekurzió érintett szintjén, dönteni kell egymáshoz való „viszonyuk” felől. Vagyis az alábbi lehetőségek – és esetleges kombinációik – közül választunk:
Az alá- és mellérendelő viszonynak több szempontból is jelentősége van. Ezek egyike az algoritmus leírási módját befolyásolja. A másik fontos következménye a bonyolultságot érinti. Míg utasítások mellérendelésével bővítve a programot, annak bonyolultságát (additíve) lineárisan növeljük, addig ugyanezen utasításokat alárendelten illesztve a programhoz, pl. egy összetett szerkezetben, (multiplikatíve) hatványozottan. Ezt tükrözi az egyik jól ismert bonyolultsági mérték: a mélységi bonyolultság, amelynek lényege, hogy a program egyes részstruktúrájához „azt a kitevőjű kettőhatványt rendeljük, ahány magasabbrendű struktúra belsejében van” [ZsL/103. o.], s e részstruktúrák összege adja ki a program összbonyolultságát.
A fenti három probléma-összetételi mód közüli választáshoz is van kezdők számára kapaszkodó: a „struktúra szerinti feldolgozás” elve [SzPZsL4/46. o.]. Az elv szoros kapcsolatot állít föl a feldolgozás alatt álló adatszerkezet és a feldolgozást szervező algoritmus-szerkezet között.
Adatszerkezet | → | Algoritmus-szerkezet |
|---|---|---|
skalár | → | függvény vagy eljárás |
direkt-szorzat | → | szekvencia |
unió | → | elágazás |
sokaság | → | ciklus |
Az elv felhasználása abból áll, hogy
Az elv használata látszólag csak az algoritmusvázlat összeállításában segít. A konkrét feladatok esetén meglévő további információ is sokszor beépíthető a hozzárendelt algoritmusba. Az elv gyümölcsöző voltát fejtegetjük a már idézett [SzPZsL4] irodalom II. fejezetében.
A programozás egyes lépései között szoros logikai kapcsolat áll fenn. Nyilvánvalóan annyival több energiánk marad a következő modell lényegi aspektusainak kibontására, minél többet tudunk kiaknázni a már kidolgozott eddigi modellekből. Ezt támogatja az információ-konverziónak nevezett gondolati eszközünk. Lényege, hogy ismerjük föl, melyek azok a korábbi modellbeli fogalmak, objektumok, amelyek jószerivel mechanikusan ültethetők át, konvertálhatók a készülő új modellbe, majd vigyük tovább ezeket.
Természetes törekvés az egyes modellekhez tartozó nyelvek kialakításánál, hogy ezek között minél több kapcsolódási pont legyen, és minél kevesebb olyan részlet, amely félrevezetheti a programépítőt a továbblépésben.
A következő kapcsolatokat vizsgáljuk meg (itt jelezzük az információ továbbvitelére alkalmazható speciális módszert):
A specifikációban szereplő állapottér-leírás (értsd: a bemeneti és kimeneti adatok együttese) kiindulópontja a tervbeli adatleírásnak. A specifikációban az alábbi halmazkonstrukciós műveletekkel szoktunk élni: direktszorzat, unió, iterált, halmaz-átnevezés, új alaphalmaz definiálás. Ezeknek feleltetjük az adatleírásban – elsősorban a típusdefinícióban – a rekord, alternatív rekord (általánosabban itt is uniónak nevezett művelet [SzPZsL4/48., 57. o.], sorozat-képzések (számos ilyent ismerünk: tömb, fájl, lista, sor, verem stb.), felsorolás-típus. Az alábbi tömör táblázattal igyekszünk világossá tenni a kapcsolatokat.
Specifikációbeli példa | Adatleírásbeli példapárja |
|---|---|
N∈N, VAN∈L | Változó N:Egész; L:Logikai |
Mag∈R* | Konstans MaxN:Egész(???) |
NyilvTart∈(Név×Nem×SzülIdo)* | Konstans MaxN:Egész(???) |
Azt, hogy szemlátomást alulról felfelé haladva szerepelnek a típusok egymásra épülése, ne tekintsük lényegi vonásnak, hiszen az adatleíró nyelvünk nem olyan szigorú, mint egy konkrét programozási nyelv. (Bár látni fogjuk a típusokkal foglalkozó részben, hogy e haladási irány szokásosnak mondható a nyelveknél.) A példában egyébként sugalljuk a módszertani tanácsot, hogy összetett adatok esetén kezdjük a legegyszerűbben elintézhetőkkel, majd a specifikációban többnyire visszafelé haladva, a már definiált típusokkal építkezzünk!
A terv és a kód adatleírásának közelsége függvénye a választott programozási nyelvnek. A közoktatásban előszeretettel használt nyelv a Pascal. Szerencsére roppant közel állnak egymáshoz, így nagyon egyszerű kódtranszformációs szabályokkal megadható az egymáshoz rendelés. [SzPTTZsL/ 6-17] Egy másik gyakori választás a C vagy a C++ esetében szintén nehézség nélkül megalkothatók a kódolási szabályok.
A tevékenységek tervbeli és kódbeli leírása közötti áttérésre az előbbiek nagyvonalakban megismételhetők. A Pascal, C, C++ nyelv esetén egyetlen komolyabban veendő különbség van: az alapfilozófia következetesen fordított volta. Amíg a tervezés javasolt stratégiája a felülről lefelé haladás, addig – pusztán fordítóprogramot egyszerűsítő okok miatt – e nyelvekben alulról felfelé kell építkezni, azaz minden fogalmat előbb definiálni, s csak azután felhasználni. E sarkalatos ponton való eltérést mégsem kell nagy didaktikai problémának venni, hiszen a kódolást a mai programfejlesztő környezetek tetszőleges sorrendben engedik elvégezni, s így már nincs különösebb jelentősége. Nem beszélve arról, hogy a kódoláshoz – ideális esetben – már csak kész algoritmus birtokában kezd neki a programozó. Így a begépelés sorrendjét érinti csupán e nyelvek „szerencsétlen” elvárása.
A specifikáció nemcsak az őt közvetlenül követő programozási lépésre hat, hanem a kód egyes részeibe is beleszól. Ugyanis a specifikációbeli előfeltétel a bemeneti adatokkal szembeni elvárásainkat tartalmazza, amit a program lényegi, transzformációs részének jogában áll elvárnia. Így tehát a kódnak garantálnia kell azt, hogy a bekerült adatok a megengedett tartományban lesznek. Ebből következik, hogy a beolvasási résznek bizony időnként a lényegi részt meghaladó bonyolultságúra kell híznia: tartalmaznia kell minden elvárás ellenőrzését elvégző kódot.
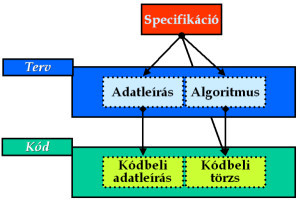Információ-konverziókAminek nincs megfizetendő ára,
annak nincs értéke sem
[Einstein]
Az intuíció a legtalányosabb, legkevésbé elemezhető gondolkodási művelet. Rá éppen az a jellemző, hogy az általa létrejött gondolatok nem valami szigorú logikát követve, többé-kevésbé „ésszerűen” bújnak elő a gondolkodó elméből. Váratlanság, meglepőség, semmihez nem hasonlítható eredetiség az ő sajátja. Bizonyára nem a semmi szülöttei, de olyan lelki mélységekből tőrnek elő, hogy pszichológus legyen a talpán, aki racionális magyarázatod tud adni: miért pont akkor, és miért pont úgy pattantak ki szülője fejéből. Állítom, hogy a gondolati mag (vagy ha nem lenne képzavar: magokat mondanék) már jóval korábban el lett ültetve, hogy a kellő időben és a kellő hívó szóra megfoganjon. Sok és intenzív agyi munka szükséges az intuíció működésbelépéséhez – erre utaltam a mottóban –, de nem tudni mennyi energia és milyen, sokszor mellékesnek tűnő gondolatsor végigjárása, mondhatni „csapongás” kell egy-egy szerencsés, intuitív gondolat megszületéséhez.
Megközelítésünkkel összecsengenek Lénárd Ferenc könyvéből vett alábbi idézet [LF/85]:
Kedrov úgy látja, hogy intuícióról akkor beszélhetünk, ha a gondolkodó úgy jut valamely igazsághoz, hogy a hozzávezető lépések számára nem tudatosak. ... Intuíció csak annál léphet fel, aki a problémával intenzíven foglalkozik, és ezért rendelkezik mindazokkal az ismeretekkel, amelyek a probléma megoldásához szükségesek. Sok anekdota-ízű példát ismerünk az intuíció szerepére tudományos felfedezéseknél. Ilyenek: Newton a lehulló alma nyomán jutott el a gravitációs törvény felfedezéséhez, Wattot a teafőző fedőjének megemelkedése juttatta a gőzerő felhasználásának gondolatához, Kekule felfedezése, ti. a szénatomok nyílt láncának gyűrűvé zárása. Kétféleképpen is jut intuíciószerű magyarázathoz. Az egyik értelmezés szerint Kekule a londoni omnibusz tetején majmokat látott egy ketrecben. Ezek élő gyűrűt alkottak egymásba csimpaszkodva. Farkaik pedig a benzolgyűrű szénatomjainak szabad vegyértékeire emlékeztette. A másik értelmezés szerint álmában saját farkába harapó kígyót látott és ez juttatta felfedezéséhez
A „csapongás” szükségességéről Pólya György ezt írja a feladatok variálásával (lásd a következő alfejezetet) kapcsolatosan:
„A figyelem összpontosítása nélkül nem lehet reményünk arra, hogy egy valamire való feladatot megoldhassunk. Ha viszont figyelmünket folyton ugyanarra a pontra irányíjuk, könnyen kifáradunk. Ahhoz, hogy figyelmünket folyton ébren tartsuk, állandóan változtatnunk kell figyelmünk tárgyát.”
Ha nincs kellő előismeretünk egy-egy szerencsés gondolat megszületésének körülményeiről, épp az hiányzik, amely lehetővé tenné, hogy a tudat mélyében fejlődő gondolat érési folyamatait, esetleg létező törvényszerűségeit elemezhessük. A fenti híres mendemondák nagy gondolkodókról és nagy gondolataik megszületéséről nyilvánvalóságokat vagy kevéssé hihető szituációkat mesélnek el. (Newton az ő almájával és a gravitációval, Watt teafőzője és a gőzerővel, Kekule a farkába harapó kígyója és a benzolmolekulával...)
Most annyira vállalkozhatunk csupán, hogy néhány algoritmikus gondolatban rejlő újszerűséget kimutassam, és létrejövetelének egy lehetséges (!) magyarázatát adjuk.
Bentley [BJ] könyvében találunk egy fejezetet, az „Aha-algoritmusok” címűt, amely rímmel az éppen feszegetett témára. A fejezetben három problémán gondolkodik el. Ezek egyike az alábbi [BJ/20. o.]:
Egy mágnesszalag legfeljebb egymillió húszbites egész számot tartalmaz véletlenszerű sorrendben. Keresnünk kell egy olyan húszbites egész számot, ami nem szerepel a szalagon...
A probléma abból keletkezik, hogy a memória nem elegendő ahhoz a kézenfekvő megoldáshoz, amely lényege a következő. Minden lehetséges (tehát a húszjegyű egész szám mindegyikéhez) rendeljünk egyetlen bittel ábrázolható „logikai” értéket úgy, hogy 0 jelentse: (eddig) nem találtuk meg benne, 1 pedig: benne van. Ekkor elegendő egyszer végigolvasva a fájlt 1-re állítani a megfelelő bitet, és amik – a kezdetben megtörtént inicializálás után – 0 értékű maradtak, azok egyike sincs a sorozatban. Ezek – mondjuk – elsőjét adja meg a program. Hogy ilyen a feladat feltételei szerint van: az biztos, hiszen húszbites szám 220 darab van, ami néhány tízezerrel az egymillió fölött van (220=1 048 576).
Tehát mit tehetünk, ha ekkora logikai tömb számára kicsi a memória? Ijedelemre semmi ok, csak keressünk valami analóg feladatot! Ilyenre azonmód ráakadhatunk, amint az az ötlet eszünkbe jut, hogy fogalmazzuk át úgy a feladatot, hogy „keressük meg azt az első értéket, amit nem találunk a sorozatban”. Ez tételekben – mint „magasszintű analógiakészlet”-ben – kifejezve: egy ’kiválasztás’ és (beleágyazva) egy ’eldöntés’ szuperpozíciója. De a megoldásunkba kicsit kritikusan belegondolunk, rájövünk, hogy borzasztóan időigényes megoldást körvonalaztunk. A legrosszabb, de nem kizárható eset, hogy a keresett elem éppen a legnagyobb lehetséges szám közelébe esik (ő az egymillió). Ekkor a kiválasztás tétel ciklusa garantáltan ennyiszer lefut, benne a hasztalan próbálkozást jelző eldöntéssel, ami a teljes sorozat beolvasását igényli. Ez 107*107=1014 darab szám fájlból olvasását jelenti, ami kivárhatatlanul hosszú idő.
A sablonok – látszólag – alkalmazhatatlanok. Ide kell az ötlet! Ha a programozó megértette, sőt a lényegét értette meg a logaritmikus keresésnek, akkor valami felsejlhet benne az esetleges alkalmazhatóságából. De ha gondolatai nem „kellően fesztelenül szárnyalnak”, azaz lepányvázzák azok a köteles sallangok, amelyek a tétel alkalmazásának feltételeit hivatottak leírni: „csak rendezett sorozatra alkalmazható, a tetejében csak közvetlen eléréssel kezelhető szerkezetben tároltra (pl. tömbre)”, akkor hamvába holt a gondolati csíra.
Ha azonban elvonatkoztat a logaritmikus keresés részleteitől, s inkább egy „hozzáállás” mintáját látja benne, akkor nyert az ötlet: megszületet az intuitív gondolat. Az algoritmus vázlata ilyesforma testet ölt: felezzük meg a teljes intervallumot (ahogy a logaritmikus keresés ötlete súgja) és számláljuk meg (nem keresünk, mert ahhoz tényleg kellenek a most fenn nem álló feltételek), hogy hány esik a számok közül az alsó, s hány a felső intervallumba. Ez egy teljes fájlolvasással oldható meg. Majd vegyük azt a felét további vizsgálatunk tárgyául, amelyikben a kevesebb számot regisztráltuk. Mármost ezt az intervallumot felezzük meg, és számláljuk az aktuális alsó és felső részbe esőket. Ez is teljes fájlolvasást igényel, de az eredeti, 220 darabot tartalmazó intervallumnak már negyedénél, 218 tartunk. Láthatjuk: 20 teljes olvasás árán egyetlen elemre fókuszáltunk. A hatékonyság növekedése tetemes: 107 a 20-hoz, azaz 50 000-szeres!
Ebben a meglepő megoldásban az intuíció egy ismert tétel (tárgyi tudás) tovább, sőt végletekig, urambocsá’ egy „filozófiává” csupaszításában (absztrahálás) öltött testet. Létrejöttéhez egy pici algoritmikus ismeretre (a logaritmikus keresésé) és nagyfokú absztrakcióra való hajlandóságra, képességre volt szükség.
A következő példát a Knuth-féle „bibliából” [KD] származik.
Ismét egy elem kereséséről van szó, de a memória a „szótár” tárolására most elegendő. Knuth a feladat megfogalmazása után egy hétköznapi ötlethez nyúl. Most nem elemzem az elementárisabb megoldás-lehetőségeket, hanem mindjárt a természetes hozzáállás knuth-i leírását idézzük [KD/436. o.]:
Tegyük föl, hogy egy szót kell kikeresnünk a szótárból. Valószínűleg nem a középső lap átvizsgálásával kezdjük a keresést, hogy azután a ¼ vagy ¾ pontban folytassuk, ahogy a bináris keresés esetén tettük. ... Ha kívánt szó A betűvel kezdődik, akkor nyilván a szótár elejéhez közel kezdjük a kutatást. Jó néhány szótárnak van »lépcsős ábécéregisztere«, amely megmutatja, hogy az adott betűvel kezdődő szavak hol találhatók. ... Tevékenységünk azonban a keresés kezdőpontjának meghatározása után sem fog hasonlítani az eddig tárgyalt módszerekhez. Ha pl. észrevesszük, hogy a kívánt szó ábécérendben jóval később van a vizsgált oldal szavainál, akkor jó sok oldalt lapozunk előre... Ez alapvetően különbözik az előző algoritmusoktól, amelyek nem tesznek különbséget a »kicsit nagyobb« és a »jóval nagyobb« között.
Ez az újszerű hozzáállás arra példa, hogy gyakran a „mindennapok racionalitása” az inspiráló tényező.
Harmadik példaként egy intuíciókban bővelkedő feladatkörből, a rendezésekéből választunk egy „nevezetes” gyöngyszemet. A feladat roppant egyszerű: rendezzünk egy N elemből álló elemsorozatot, amelyet a memóriában tartunk, valamilyen közvetlen elérésű struktúrával ábrázolva (ilyen, pl. a tömb). A „hagyományos” rendező algoritmusok „átlagos rendezetlenségű” sorozattal nem túl hatékonyan: O(N2) hasonlítással és mozgatással birkóznak meg, az „ideális”: O(N*ln(N)), illetve O(N) helyett. Itt a kihívás egy algoritmus-feltaláló számára. Nézzük meg, Floyd fejében mily ötletek cikáztak, amikor 1964 tájékán kitalálta a kupac-rendezés algoritmusát! [KD/161. o.]
Az algoritmusa azon az ismert tény kiküszöbölését célozta meg, hogy a rossz hatékonyságnak legfőbb oka a sok felesleges vizsgálat (és csere). Felesleges az a vizsgálat, amely eredménye az eddigi vizsgálatok után már ismert, vagy kikövetkeztethető (kellene, legyen). Az ’eredmény ismert’ alatt azt értjük, hogy két már összehasonlított elemet újból összevet az algoritmus. Erre sor kerülhet akkor, ha az algoritmus odébb tesz két elemet (és erre a tényre nem fordít figyelmet), majd később újból hasonlításra jelöl ki (figyelmetlensége folytán). Kikövetkeztethető lenne két elem sorrendi viszonya, ha kihasználná (képes lenne kihasználni) a rendezés tranzitivitását, azaz hogy ai≤aj és aj≤ak (tényleges ellenőrzés nélkül) következik ai≤ak. A hatékony algoritmusok mindegyike ezt a problémát küszöböli ki. Floyd agyában is ez keringett. De mi még? Valószínűleg egy kép, amely a sorozatot úgy ábrázolta, hogy a rendezettség vagy valami hozzá hasonló könnyen leolvasható legyen.
Ez a kép itt központi szereplője a történetnek, ezért hadd időzzünk el rajta! Úgy hisszük, az algoritmusbeli elem-összehasonlítások miatt egy olyan bináris fa képe rajzolódott ki Floyd lelki szemei előtt, amelyben a gyökér gyerekei rendezettségben egyformán viszonyulnak (pl. mindketten nagyobbak) a szülejükhöz. Az világos, hogy e lokális rendezettségi viszony nem jelenthet egyben globális rendezettséget is, mert ez a kívánt végállapot lenne; ez kezdetben, sőt több lépésen át közben sem jellemezheti a sorozatot. Igenám, de ha ez a „lokális” viszony a fa minden (nem levél) elemére teljesül, akkor az egyetlen globális gyökérelemre nézve valami kitüntetettet jelenthet. (Itt azt kell közbevessük: eddig könnyen hihető, hogy e kép intuitíve pattanhat ki a gondolkodó fejéből. Annak pillanatszerű belátása, hogy e globális tulajdonság valóban az, amit érezhet az ötletgazda: a gyökér egyben globális minimum elem is, nem valószínű, bár nem is kizárt. Inkább azt szeretnénk hinni, Floyd nekilátott, és akkurátusan bebizonyította sejtését.)
A bináris fa ötletét a szerző azon korábbi tapasztalata erősíthette (közbevetés: lehet, hogy ez is a mesemondó fikciója, de Floyd személyes vallomása híján, mi mást tehetne, mint logikus előfeltételek után tapogat?), hogy – mondjuk – a kereső fákkal foglalkozván tudta, egy N-elemű fa levéleleméig eljutni ideális esetben nagyon gyorsan lehet: O(log2N) lépésben. Ideális, ha teljesen kiegyensúlyozott. (Képszerűen: egy tökéletes háromszög-alakban rajzolható meg.)
Véleményem szerint eddig az intuíció. Ezt követően jött a dolgos „szelídítése” az algoritmusnak, ami éppennyire csodálatos teljesítmény, de legalább beláthatóan logikus, azaz „emberi”. Ezekből az algoritmus hangolgatós lépésekből csak azt emelném ki, amely ismét Floyd gondolati fesztelenségét mutatja: tudta a bináris fát „linearizálva” is látni, amely szükséges volt a könnyed algoritmus elkészítéséhez.
E példában az „aha”-élményhez egy meglepő adatszerkezet kellett, amit a tetejében kétféleképpen is értelmez és vizualizál a feltaláló. A filozófia szintjén: síkbeliként, az algoritmus részletezésénél már: egy dimenziósként, „kiegyenesítve”.
Összefoglalva a fentieket: a felfedező szinte mindig azzal jut el meglepő gondolatokig, hogy látszólag össze nem illő dolgokat képes „gátlástalanul” összekapcsolni. Egy „definíció” szerint alkalmazhatatlan algoritmust erőltet sikerrel, vagy egy hétköznap beváló hozzáállást valósít meg számítástechnikai probléma-környezetben, vagy egy, a feladathoz egyáltalán nem illő „kép” köré építi föl algoritmikus gondolatait...
Hadd kezdjük néhány ide illő, Pólya Györgytől [PGy1/114-115.o.] és Lénárd Ferenctől [LF/62. o.] vett idézettel:
A feladat variálása lényeges dolog. Ennek több oka is van. Így a feladat megoldásában való előrehaladásunk bizonyos szempontból abban áll, hogy mozgósítjuk és megszervezzük már egyszer megszerzett tudásanyagunkat. Fel kell idéznünk bizonyos emlékképeket, és bele kell dolgozni a feladatba. A feladat variálása segítségünkre van abban, hogy ez sikerüljön. Hogyan?
Az emlékezés folyamata egyfajta »kontakthatáson«, »asszociáción« alapszik. ... A feladat változtatása során új szempontok felvetésével új kontaktusokat, érintkezési pontokat, kapcsolódásokat, a feladat szempontjából fontos elemek új asszociációs lehetőségeit nyitjuk meg.
A különböző problémák, feladatok megoldása során a variálások lehetővé teszik, hogy pontosabban ismerjük meg ezeket a problémákat, feladatokat. Enélkül nem találjuk meg a megoldáshoz vezető úton a lehetőségeket, amelyekkel élve eredményhez is jutunk.
Hogyan értelmezzük szavaikat a programozás vonatkozásában? Elsősorban a programkészítés tervezési fázisára gondolhatunk, amely során egyrészt a megfelelő adatszerkezeteket, ezek ábrázolását, típusát (lásd az adatabsztrakcióról szóló fejezetet), és rájuk épülő algoritmust kell körvonalaznunk, egyre mélyebbre hatolva, egyre finomabb bontásban. (Lásd az Algoritmikus absztrakció alfejezetben a felülről lefelé tervezésről mondottakat.)
A rutintalan programozó a tételek megismerése előtt gyakorta a megfelelő algoritmikus szerkezet kiválasztásánál is variálja az általa elképzelhetőnek tartottakat, s megvizsgálja egyenként őket, melyik írja le az elképzeléseit maradéktalanul. Később a tételek szintjén vetődik föl ugyanez a helyes(ebb) séma megtalálása érdekében. Ahogy bonyolódnak a feladatok, úgy növekszik a variációs lehetőségek száma, nehezebbé válik a megfelelő kombináció kiválasztása. Kellően komplex feladat célirányos megoldása már csak sok gyakorlat érlelte tudás birtokában képzelhető el. Ahogy a sakknagymesterek eredményességét sem elsősorban a programozási tételszerű nagyobb lexikai tudás, azaz az ’álláskombinációk és sikeres válaszlépések’ arzenáljának ismerete okozza, hanem ezek kombinálás képességének fejlettebb volta. (Aminek ha nem is elegendő, de biztosan szükséges feltétele a kitartó gyakorlás, állásértékelés.)
Sajátos variálás az, amire azért van szükség, mert a tervezéskor zsákutcába jutott a programozó, s kényszerűségből újabb variánst kell találnia a már egyszer meggondolt, de sikertelennek talált részfeladatra. (Gondoljunk a programkészítési elvek közül a „vissza az ősökhöz” taktikai elvre!) [SzPZsL1/96. o.]
Másik tipikus programkészítési fázis, amelyben a variálás fontos gondolkodási technika: a program hatékonysági vizsgálata. Ekkor több megoldási lehetőséget azért vesz számításba a programozó, hogy ezeket „megversenyeztesse”, s így jusson a legalkalmasabb megoldáshoz.
Elgondolkodtató biológiai párhuzam vehető észre a gondolatok variálására. Gondolatvariálás célja: a gondolat újabb, életrevalóbb változatának létrehozása, amely a gondolatszelekció során megméretik a többi, ugyanazt célzó gondolattal, azaz az erősebb, a problémához jobban illő kiszorítja a satnyábbakat. A gondolatvariáció és a gondolatszelekció két, ily módon egymást támogató tényezője a gondolatevolúciónak.
  |
 |
 |
A tananyag az ELTESCORM keretrendszerrel készült