Egyirányú, fejelemes lista (FL) rendezése növekvő sorrendbe, beszúró rendezéssel.
Három változatot nézünk meg, egyre nagyobb hatékonyságú algoritmust készítve.
Megoldási ötlet: az üres lista nyilván rendezett, továbbá tanultuk a rendezett listába történő beszúrás algoritmusát. legyen tehát az algoritmus a következő: állítsunk egy bejáró pointert az első elemre, majd az eredeti listánkat állítsuk üresre (a fejelem next pointerét NULL-ra kell állítani), és ebbe az üres listába szúrjuk be az eredeti első elemet, az így kapott listába szúrjuk be a második elemet, majd ezt folytatjuk, amíg az eredeti lista valamennyi elemét be nem szúrtuk.

Beszúr függvény végzi a "q" paraméterben kapott elem befűzését a rendezettség szerinti helyére. Annyi az eltérés a gyakorlaton megbeszélt beszúráshoz képest, hogy most a függvény második paramétere egy listaelem címe, amit mindenképp befűzünk a listába, a rendezettségnek megfelelő helyre:

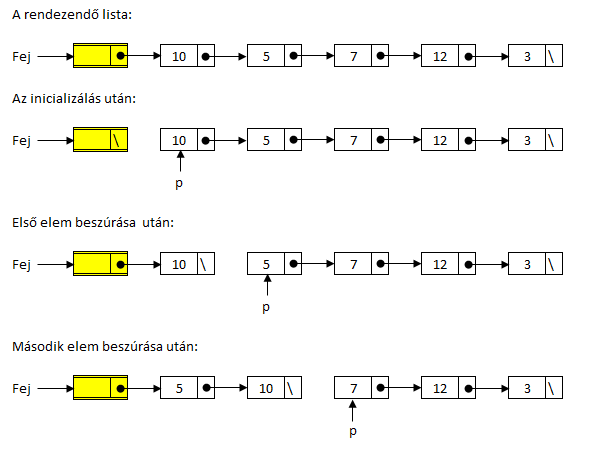
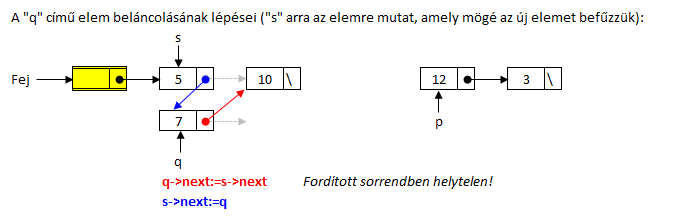
Észrevehető, hogy egy menetet megspórolunk, ha a tömbös rendező algoritmushoz hasonlóan, az elemek beszúrását a második elemmel kezdjük, hiszen az egy-elemű lista biztosan rendezett. Ekkor viszont külön kell arra is gondolni, hogy esetleg üres a lista. (Ez tömb esetén fel sem merült, viszont listáknál előfordulhat.) Hogy ilyenkor is helyesen működjön a megoldásunk, indításkor az első lépés, hogy elleőrizzük, nem üres-e a lista.
Csak a felső szint változik, így csak azt adjuk meg, a meghívott "Beszúr" függvény ugyanaz lesz.
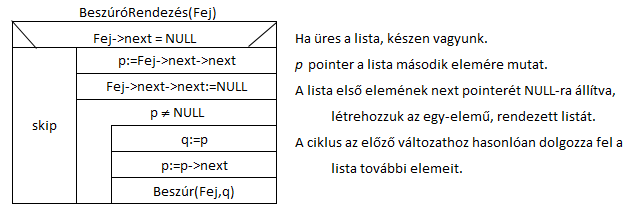
Tehát csak az indulás változott!
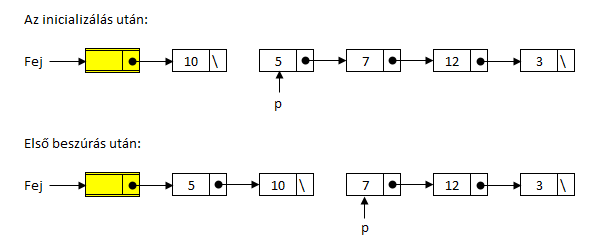
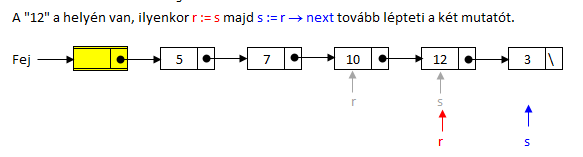
Észrevehető, hogy amikor a beszúrandó elem nagyobb, mint a már rendezett listánk utolsó eleme, a beszúró függvény végig lépeget a teljes rendezett listán, hogy eljusson az utolsó elemhez, ami után befűzi a beszúrandó elemet. Lásd a fenti példában, amikor a 12-t dolgozza fel az algoritmus. Ez elég gyakran előfordul, érdemes tehát elgondolkodni azon, hogyan tudjuk kihasználni, hogy ilyenkor a "helyén" van az elem. A tömbös beszúró rendezés,is figyelt erre az esetre! Átalakítjuk úgy az algoritmust, hogy nem szakítjuk meg a láncot a rendezett listarész és a rendezezésre váró listarész között, hanem lesz egy pointerünk (r), amelyik a rendezett listarész utolsó elemére mutat, illetve lesz egy bejáró pointer (s), amelyik az épp beszúrandó elemre mutat. Ha az r című elem tartalma kisebbegyenlő, mint az s című listaelem tartalma, akkor nem kell a beszúrást elvégezni, a két pointer léphet tovább. Ha nem, akkor az r című elem mutatóját az s című elem után következőre állítjuk (s című elemet kifűzzük), majd megkeressük az s című elem helyét a lista elejéről indulva. Biztosan tudjuk, hogy lesz nála nagyobb (az r című elem biztosan ilyen), így egy sokkal egyszerűbb, kiválasztás tételre alapozott ciklussal addig megyünk, amíg az s-nél kisebb elemeket át nem lépjük. Ennek a változatnak az is jó tulajdonsága, hogy az egyenlő értékű elemek sorrendjét megtartja, az ilyen tulajdonságú rendező algoritmusokat nevezik stabil rendezőknek.
Lássuk tehát a legügyesebb megoldást:
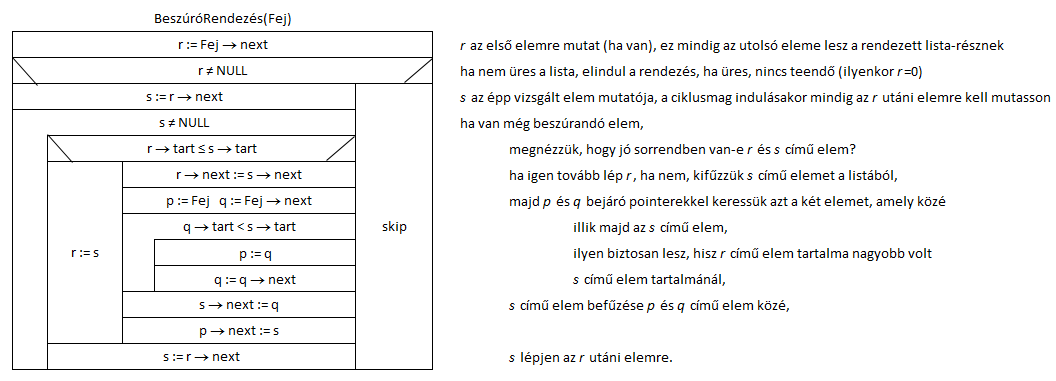
Az algoritmus működésének illusztrációja:
Nézzük meg az algoritmus indítását, r az első elemre, s a másodikra mutat:

Az s című elem tartalma kisebb, mint az r című elemé, tehát a hamis ágon megyünk tovább, figyeljük meg a belső ciklus működését:

Az algoritmus külső ciklusának folytatása, a pointerek állása a ciklusmag végén:
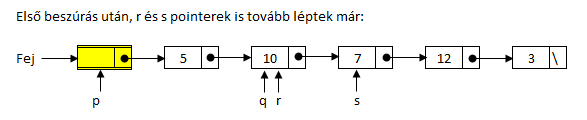
Jön a "7"-es elem beszúrása az r pointerig tartó rendezett részbe. Nézzük most meg az elem befűzésének menetét részletesen:
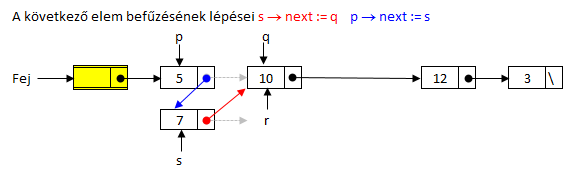
A lista következő eleme a helyén van, nem kell átfűzni. Ilyenkor a külső ciklus magjának igaz ágát hajtja végre az algoritmus, a rendezett lista eggyel nő, s pedig az r utáni elemre lép.