Prímszámok meghatározására egy adott 1..n intervallumban ismeretes az "Eratoszthenészi szita" algoritmus. Felírjuk egy lapra 2-től n-ig az egész számokat növekvőleg. 2 prím, kihúzzuk 2 többszöröseit. A következő még át nem húzott szám prím, ez most a 3, kihúzzuk a többszöröseit. A következő át nem húzott az 5, ez is prím, többszöröseit áthúzzuk. Ezt folytatva, a papíron maradt számok lesznek 2-től n-ig a prímszámok. Tömbben elhelyezve a számokat nem is kell osztást végeznünk, egyszerűen az adott értékkel (2,3,5...) lépkedve "kihúzzuk" a számokat a tömbből.
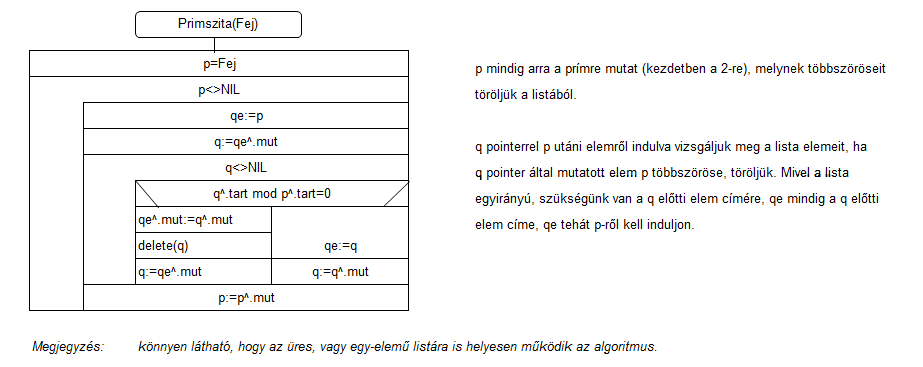
Ennek mintájára készítsünk algoritmust, mely egy listában állítja elő a prímeket: adott egy egyirányú, fejelem nélküli lista, első elemére "Fej" pointer mutat. A lista a természetes számokat tartalmazza 2-vel kezdve. Induljunk 2-ről, és fűzzük ki a listából a 2 többszöröseit. A következő listán maradt szám a 3, ez prím, fűzzük ki három többszöröseit, a következő az 5, ennek többszöröseivel folytatjuk, mindaddig, míg a lista végére nem érünk.
