Bináris fák

Bináris fák ábrázolása láncoltan

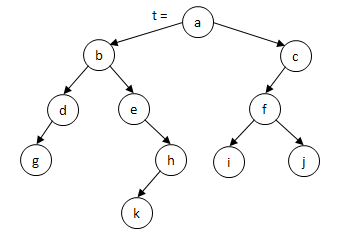
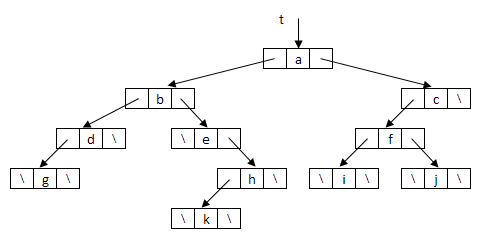
A bináris fa láncolt ábrázolása történhet két pointerrel, egyik pointer a bal oldali gyerekre, a másik pointer a jobb oldali gyerekre mutat. Ekkor egy irányított gráfként ábrázoljuk a fát.
bináris fa irányított élekkel bináris fa két pointerrel ábrázolva
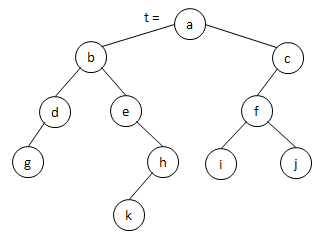
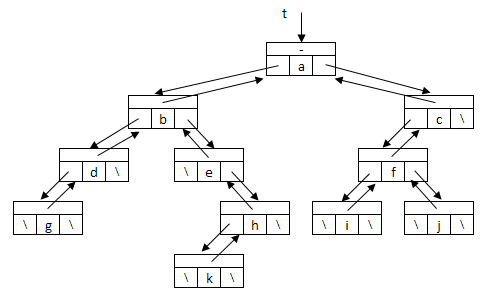
A bináris fa láncolt ábrázolása történhet három pointerrel, egyik pointer a bal oldali gyerekre, a másik pointer a jobb oldali gyerekre mutat, a harmadik pedig a szülőre. Ekkor egy irányítatlan gráfként ábrázoljuk a fát.
bináris fa irányítatlan élekkel bináris fa ábrázolása három pointerrel

Az algoritmusokban használt jelölések

Ha láncoltan ábrázoljuk a bináris fát, akkor bejáráshoz pointereket használhatunk. Ha p a fa egy csúcsára mutató pointer, akkor:

Ábrázolás szintjén
megadott művelet		 Adatszerkezet szintjén
megadott művelet		 Jelentése
p → bal bal(p) p bal oldali részfája
p → jobb jobb(p) p jobb oldali részfája
p → szülő szülő(p) p szülője
p → kulcs kulcs(p)
vagy kulcs(gy(p))		 p csúcsban tárolt kulcs, kulcs(p) helyett
használatos a kulcs(gy(p)) jelölés is,
hisz ilyenkor "p" egy fát szimbolizál, gy(p)
ennek a részfának a gyökerét jelenti
p = NIL,NULL,0 p = Ω a részfa "üres"

Nevezetes fabejáró algoritmusok

A bináris fákkal kapcsolatos feladatok megoldásai a három nevezetes rekurzív bejáró algoritmuson, és az iteratív szintfolytonos bejáró algoritmuson alapulnak

preorder bejárás inorder bejárás postorder bejárás
szintfolytonos bejárás  

Kifejezés fa

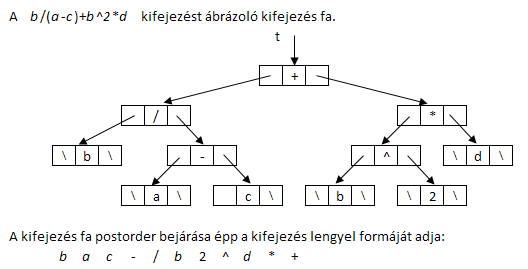
Feltéve, hogy egy aritmetikai kifejezésben két-, esetleg egy-operandusú műveleti jelek (operátorok) fordulhatnak elő, a kifejezés ábrázolható egy bináris fával, ezt hívjuk kifejezés fának. A kifejezés fa összefügg a tanult lengyel formával, ugyanis megfigyelhető, hogy a kifejezés fa postorder bejárásával előállítható a lengyel forma, és fordítva is igaz, a lengyel formából felépíthető a kifejezés fa.

kifejezés fa

Gyakorló feladatok

I. Fa felépítésével, bejárásval kapcsolatos gyakorló feladatok

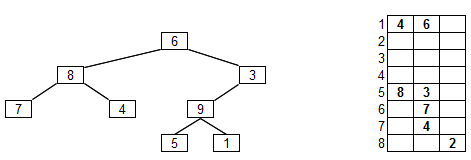
  1. Az ábrán látható bináris fát egy 8 x 3 -as tömbben ábrázoltunk. A középső oszlop tartalmazza a csúcsban tárolt kulcsot, az első oszlop a bal oldali gyerek indexe, a harmadik oszlop a jobb oldali gyerek indexe. Az index helyére nulla kerül, ha nincs az adott irányban leszármazottja a csúcsnak. Töltse ki a tömb hiányzó értékeit. (Kezdő feladat.)
    A fa ábrája
    megoldás
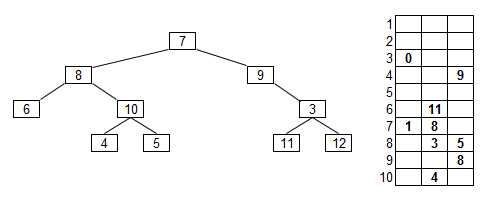
  2. Az ábrán látható bináris fát egy 10 x 3 -as tömbben ábrázoltunk. A középső oszlop tartalmazza a csúcsban tárolt kulcsot, az első oszlop a bal oldali gyerek indexe, a harmadik oszlop a jobb oldali gyerek indexe. Az index helyére nulla kerül, ha nincs az adott irányban leszármazottja a csúcsnak. Töltse ki a tömb hiányzó értékeit. (Haladó feladat.)
    A fa ábrája
    megoldás
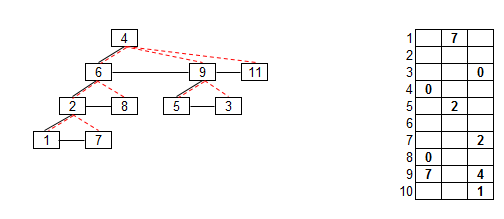
  3. Az ábrán látható nem bináris fát egy 10 x 3 -as tömbben két pointer segítségével ábrázoltunk. A középső oszlop tartalmazza a csúcsban tárolt kulcsot, az első oszlop a csúcs "első" gyerekének indexe, a harmadik oszlop a csúcs "testvérének" indexe. Az index helyére nulla kerül, ha nincs gyereke illetve nincs testvére a csúcsnak. Töltse ki a tömb hiányzó értékeit. (Nehéz feladat.)
    A fa ábrája
    megoldás

  4. Milyen sorrendben írná ki a három nevezetes rekurzív bejáró algoritmus az alábbi fa csúcsainak azonosítóját?
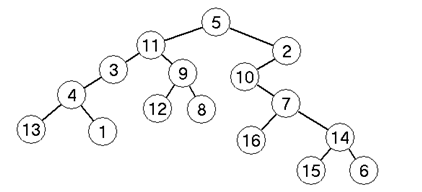
    bináris fa képe
    megoldás

  5. Egy (nem teljes) bináris fa postorder és inorder bejárása a következő sorozatokat eredményezte, rajzolja le a fát!
    POSTODER:   17,   4,   7,   9,   45,   91,   2,   8,   53,   10,   66,   72,   34,   5,   3
    INORDER:         17,   8,   4,   7,   91,   45,   9,   2,   3,   5,   34,   53,   66,   10,   72
    megoldás lépésről lépésre, részletesen

  6. Milyen sorrendben írná ki a három nevezetes rekurzív bejáró algoritmus az alábbi fa csúcsainak azonosítóját?
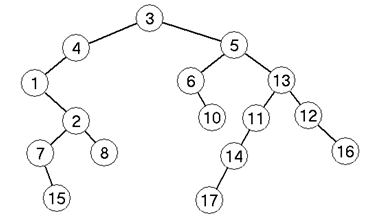
    A fa ábrája

  7. Egy (nem teljes) bináris fa preorder és inorder bejárása a következő sorozatokat eredményezte, rajzolja le a fát!
    PREORDER:   D   E   M   L   A   H   P   B   K   G   N   Q   C   F
    INORDER:      L   M   H   A   E   D   B   G   K   N   P  C   F   Q
    megoldás

II. Rekurzív algoritmus készítésére gyakorló feladatok

  1. Készítsünk rekurzív függvényt, amelyik megszámolja egy bináris fában a a) csúcsokat b) leveleket.

  2. Készítsünk rekurzív függvényt, mely megadja egy bináris fa adott szintjén lévő a) csúcsok b) levelek számát.

  3. Adott két bináris fa. Készítsünk logikai értékű rekurzív függvényt, mely eldönti, hogy azonos-e a szerkezetük.

  4. Készítsünk rekurzív függvényt, mely megadja egy bináris fa csúcsaiban (belső pontjaiban, leveleiben) szereplő értékek maximumát.

  5. Készítsünk rekurzív függvényt, mely meghatározza azt a legkisebb magasságot, amelyben egy megadott bináris fa már tartalmaz levelet. (Üres fára ez az érték legyen -1, egy pontból álló fára pedig nulla.)

  6. Készítsünk rekurzív függvényt, mely eldönti egy bináris fáról, hogy piramis-e. (Minden belső csúcsban kisebb vagy egyenlő érték található, mint a gyerekeiben.)

  7. Adott egy kifejezésfa. Készítsünk rekurzív elárást, mely kiírja a kifejezés teljesen zárójelezett alakját. (Az operandusok nincsenek zárójelben.)

III. Iteratív algoritmus készítésére gyakorló feladatok

  1. Adott egy kifejezés lengyel formája egy szekvenciális input sorozatban. Készítsünk iteratív eljárást, mely felépíti a kifejezésfát.

  2. Készítsük el a preorder rekurzív bejáró algoritmus iteratív változatát.

  3. Készítsük el az inorder rekurzív bejáró algoritmus iteratív változatát.

  4. Készítsük el a postorder rekurzív bejáró algoritmus iteratív változatát.