Bináris keresőfák, AVL fák

Egy bináris keresőfa

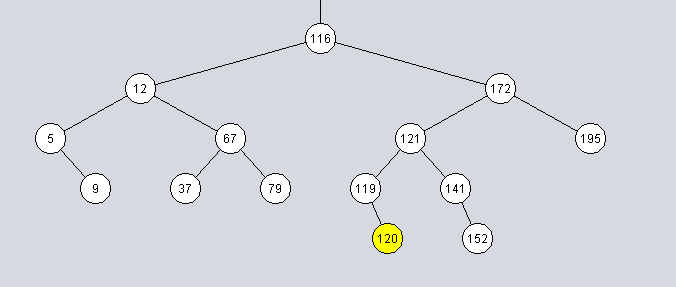
Egy AVL fa

• Első példa AVL fa felépítésére kulcsok egymás utáni beszúrásával.
  
  
• Második példa AVL fa felépítésére kulcsok egymás utáni beszúrásával.
  
  

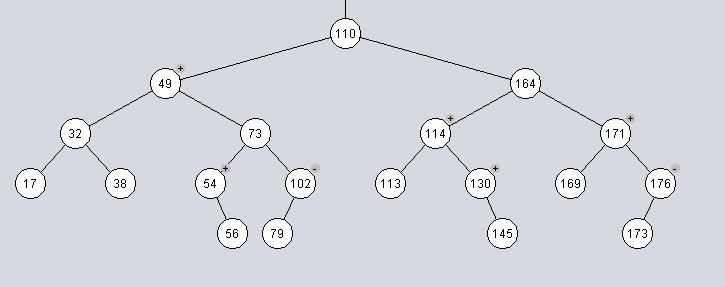
Gyakorló feladatok

1. a) Egy bináris kereső fa preorder bejárása a következő sorozatot eredményezte:
   PRE: 52,  20,  31,  25,  22,  43,  35,  46,  80,  75,  60,  79,  84,  93,  86
   Rajzolja le a fát!
   megoldás
   b) Építsen bináris keresőfát egymás utáni beszúrásokkal az alábbi kulcsokból:
   75,  43,  22,  63,  10,  37,  68,  85,  88,  49,  40,  56,  39,  52,  15,  38
   Törölje a 43-as csúcsot a tanult algoritmus szerint, majd rajzolja le újra a fát. 
   megoldás
   
   
2. a) Egy bináris keresőfa postorder bejárása a következő sorozatot eredményezte:
   POST: 20,  35,  22,  18,  50,  48,  47,  39,  60,  54,  74,  71,  79,  76,  82,  63,  52
   Rajzolja le a fát!
   megoldás
   b) Törölje a tanult algoritmus szerint a 63-as csúcsot, majd rajzolja le újra a fát.
   megoldás
   
   
3. Készítsen rekurzív algoritmust a következő feladatra: egy bináris keresőfa 0..k szintjein lévő kulcsokat kell kiírni nagyság szerint csökkenően. Módosítsa a tanult rekurzív bejáró algoritmusok közül a megfelelőt a feladat szerint. (A gyökér szintje 0.)
   megoldás
   
   
4. Készítsen rekurzív algoritmust a következő feladatra: egy bináris keresőfa n..m szintjein elhelyezkedő kulcsokat kell kiírni nagyság szerint növekvően. Módosítsa a tanult rekurzív bejáró algo-ritmusok közül a megfelelőt a feladat szerint. (0≤n≤m, a gyökér szintje 0)
   megoldás
   
   
5. Írjon rekurzív egész értékű függvényt, mely minél kevesebb összehasonlítással megadja, hogy egy tetszőleges t keresőfában hány kulcs esik bele egy előre adott [a,b] intervallumba. Nem fogadható el az a megoldás, mely valamely tanult stratégia szerint bejárja a fát, és közben vizsgálja a csúcsok-ban tárolt értékeket, használjuk ki a keresőfa alakjáról tanultakat!
   első megoldás        második megoldás
   
   
6. Adott egy rendezett számsorozat az A[1..n] tömbben, a számok mind különbözők. Adjon rekurzív algoritmust, mely a rendezett tömbből felépíti az optimális alakú láncolt ábrázolású kereső fát. A fa csúcsait három pointerrel ábrázoljuk: bal, jobb és szülő pointerekkel.
   
   
7. A tanult algoritmus alapján építsen a következő számsorozatból AVL fát. Feltétlenül jelezze minden forgatás előtt a fa csúcspontjainak egyensúlyát, jelölje a transzformációban résztvevő részfát, és adja meg a forgatás típusát.
   74   86   24   56   12   8   99   76   80   110   20   18   22   3   15
   
   
8. Adott egy bináris keresőfa preorder bejárásával keletkezett kulcssorozat egy tömbben. Készítsen rekurzív algoritmust, mely felépíti a láncoltan ábrázolt bináris keresőfát a tömb alapján. A csúcsokat 2 pointerrel ábrázoljuk, szülő pointer nincs.
   
   
9. Adott egy bináris keresőfa postorder bejárásával keletkezett kulcssorozat egy tömbben. Készítsen rekurzív algoritmust, mely felépíti a láncoltan ábrázolt bináris keresőfát a tömb alapján. A csúcsokat 2 pointerrel ábrázoljuk, szülő pointer nincs.
   
   
10. Adott egy láncoltan ábrázolt bináris keresőfa. A fát három pointerrel (balgyerek, jobbgyerek, szülő) ábrázoltuk. Készítsen iteratív algoritmust, mely megadja a bináris keresőfa egy adott elemének rákövetkezőjét. Rákövetkező alatt azt az elemet értjük, mely nagyság szerint növekvő sorrendben az adott elem után következik.
    
    
11. Adott egy láncoltan ábrázolt bináris keresőfa. A fát három pointerrel (balgyerek, jobbgyerek, szülő) ábrázoltuk. Készítsen iteratív algoritmust, mely megadja a bináris keresőfa egy adott elemének előzőjét. Előző alatt azt az elemet értjük, mely nagyság szerint növekvő sorrendben az adott elem előtt állna.