Műveletigény, aszimptotika

1. Elemezzük a programozásból tanult elemi  programozási tételek műveletigényét.
   
   1. Összegzés megoldás
   2. Megszámolás
   3. Maximum kiválasztás
   4. Lineáris keresés
   5. Logaritmikus keresés összehasonlításainak számát
   
   A tételek specificikációját, algoritmusát Gregorics Tibor által, a programozás tárgyhoz készített segéd anyagból vettük át. http://people.inf.elte.hu/gt/prog/progtetel_intervallum.pdf
   


2. Elemezzük a buborék rendezés egyszerű változatát. Hány összehasonlítást és cserét végez az algoritmus legjobb/legrosszabb/átlagos esetben? Az átlagos eset vizsgálatához feltehetjük, hogy minden elem különböző és minden permutáció ugyanolyan valószínűségű.
   
   
3. Készítsük el a buborék rendezés következő, módosított változatának algoritmusát. A belső ciklusban megjegyezzük az utolsó csere helyét, hiszen tudhatjuk, hogy utána már az elemek rendezettek, így a következő menetben elég az utolsó csere helyéig vizsgálni az elemek sorrendjét. Hány összehasonlítást és cserét végez a módosított algoritmus legjobb/legrosszabb esetben?
   


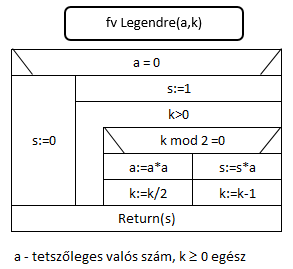
4. A számítógépes matematikai eljárások egy valós szám nemnegatív egész kitevős hatványát ügyes ismételt szorzásokkal számítják ki úgy, hogy közben magát a kitevőt kettő hatványainak összegeként alakítják ki. Határozzuk meg, hogy az alábbi Legendre-algoritmus hány szorzást végez a legjobb és a legrosszabb esetben.
   
   


5. Készítsük el a maximum kiválasztó rendezés algoritmusát A[1..n] tömbre. Elemezzük hány összehasonlítást és cserét végez az algoritmus.


6. Bizonyítsuk be az aszimptotikus függvényosztályok alábbi tulajdonságait:
   1. Reflexivitás: Θ, Ο, Ω
   2. Tranzitivitás: Θ, Ο, Ω
   3. Szimmetria: Θ
   4. Ο és Ω közötti "felcserélt" szimmetria: f(n) ∈ Ο(g(n)) ⇔ g(n) ∈ Ω(f(n))
   
   
   
7. Bizonyítsuk be, hogy az Ο, Ω, Θ függvényosztályok zártak az összeadásra és a pozitív számmal való szorzásra nézve. Például legyen f ∈ Ο(g) és h ∈ Ο(g) , valamint c > 0. Lássuk be, hogy ekkor f+h ∈ Ο(g), ill. c*f ∈ Ο(g).
   
   
8. Lássuk be, hogy polinom esetén a legmagasabb fokú tag meghatározza a nagyságrendet:
   a_k*n^k + a_k-1*n^k-1 + ...+ a₁*n + a₀ = Θ(n^k)
   
   
9. Lássuk be, hogy log_an=Θ(log_bn), ahol a,b > 1 . (A logaritmus alapszámának nincs szerepe az aszimptotikus viselkedés szempontjából.)
   
   
10. Lássuk be, hogy n^a ∈ Ο(n^a+ε) és n^a ∉ Θ(n^a+ε), a ≥ 0 és ε > 0 esetén. (Polinomiális lépésszám esetén a legmagasabb fokú tag kitevőjében a legcsekélyebb változás is éles aszimptotikus változást eredményez.)
    
    
11. Lássuk be, hogy az összegben a nagyobbik függvény határozza meg az aszimptotikát. Ha szekvenciába rakunk két algoritmust, melyek futási ideje f(n) illetve g(n), akkor aszimptotikus viselkedés szempontjából a kettő együtt a nagyobbik nagyságrendbe fog tartozni.
    f(n) + g(n) = Θ (max(f(n),g(n)))
    
    
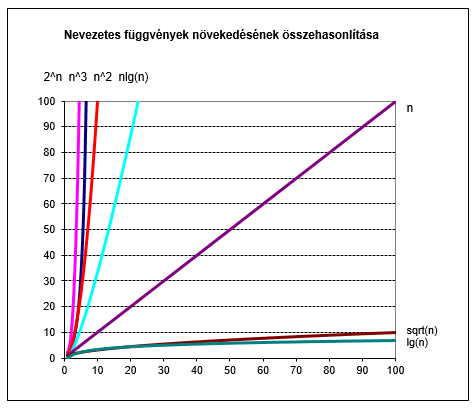
12. Adottak a következő fiktív futási idők:  lg(n),   √n,   n,   n*lg(n),   n²,   n³, 2ⁿ
    Számítsuk ki, hogy 1 000 000 művelet / mp műveleti sebességet feltételezve, mennyi ideig futna a megoldás n=10, 100, 1000, 10000 adatra. Fejezzük ki a futási időt valamely "értelmes" időegységben (mp, perc, óra, nap, év).
    megoldás
    
    
13. Rendezze aszimptotikusan növekvő sorrendbe az alábbi függvényeket, ha vannak köztük egyenlők, azt is jelölje:
    
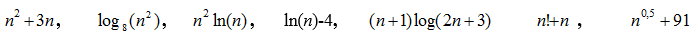
    megoldás
    
    
14. Igazoljuk: 3n³+2n²-3n-1 = Θ(n³)
    (Adjunk konkrét c₁, c₂ konstansokat, és n₀ értéket!)
    
    
15. Rendezze aszimptotikusan növekvő sorrendbe az alábbi függvényeket, ha vannak köztük egyenlők, azt is jelölje:
    
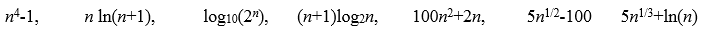
    megoldás
    
    
16. Rendezze aszimptotikusan növekvő sorrendbe az alábbi függvényeket, ha vannak köztük egyenlők, azt is jelölje:
    
    
    
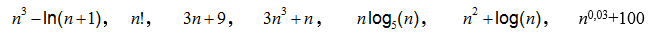
17. A megfelelő definíciók alapján igazolja, vagy cáfolja:
    3ⁿ = Ω(2ⁿ)
    3ⁿ = Θ(2ⁿ)
    
    
18. A megfelelő definíció alapján igazolja, vagy cáfolja:
    2ⁿ⁺¹ = O(2ⁿ)
    2²ⁿ = O(2ⁿ)
    
    
19. Igazolja a következő állítást:
    lg(n!) = O(n log(n))
    
    
20. A definíció alapján mutassa meg, hogy
    n³ + 2n² - n ≠ Θ(n²)
    Mit kellene Θ helyett írnunk, hogy igaz legyen az egyenlőség?