Prioritásos sor, kupac

Példa feladat:
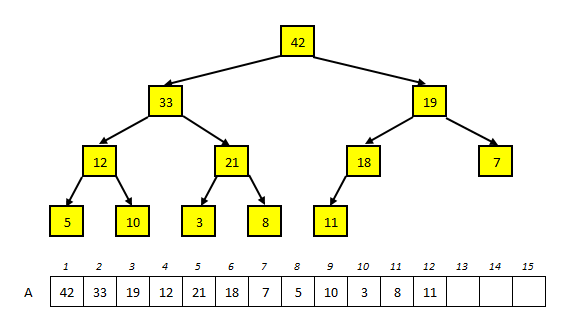
Maximum kupaccal ábrázoltunk egy prioritásos sort. A kupac képe illetve a
kupac elhelyezkedése a tömbben az alábbi ábrán látható.
-
Tegyük be a prioritásos sorba a 24-et. Mutassa be, hogyan történik az elem
beszúrása a kupacba! Adja meg az eredményül kapott kupacot bináris fával
ábrázolva, és tömbösen is.
-
Az eredeti prioritásos sorból kivesszük a legnagyobb elemet. Mutassa be,
hogyan történik a legnagyobb elem kivétele, illetve a kivétel után a kupac
helyreállítása. Adja meg az eredményül kapott kupacot bináris fával ábrázolva,
és tömbösen is.
Feladatok
- Készítse el a prioritásos sor műveleteit megvalósító algoritmusokat, úgy, hogy rendezetlen résztömbbel ábrázolja
a prioritásos sort. A sorban lévő elemek mindig a tömb elején helyezkedjenek el,
rendezetlen sorrendben. Egy index tárolja mindig a legnagyobb elem indexét.
A
max() függvény műveletigénye: Θ(1), maxKivesz(): Θ(n),
prSorba(x): Θ(1)
- Készítse el a prioritásos sor műveleteit megvalósító algoritmusokat, úgy, hogy rendezett résztömbbel ábrázolja
a prioritásos sort. A sorban lévő elemek mindig a tömb elején helyezkedjenek el,
növekvően rendezett sorrendben.
A max() függvény műveletigénye: Θ(1),
maxKivesz(): Θ(1), prSorba(x): Θ(n)
- Készítse el a prioritásos sor műveleteit megvalósító algoritmusokat, úgy, hogy kupaccal ábrázolja
a prioritásos sort.
A max() függvény műveletigénye: Θ(1), maxKivesz(): O(log2n),
prSorba(x): O(log2n)
-
Egy prioritásos sort
kétirányú, rendezett, fejelemes listával ábrázolunk. A lista egy elme
(kulcs, prioritás, előremutató, visszamutató) négyesből áll. A lista prioritás
szerint csökkenőleg rendezett. Adja meg a következő műveletek struktogramját:
Üres(PS)-létrehozza az üres sort, Betesz(PS,kulcs,prior)-beteszi a sorba az
adott kulcsú és prioritású elemet. Ügyelni kell arra, hogy ha van már a sorban
ilyen kulcsú elem, akkor nem szabad még egy példányban betenni a sorba, hibát
kell jelezni. Kivesz(PS,kulcs)-kiveszi a legnagyobb
prioritású elemet, ha a sor üres, jelezzen hibát, PriorNövel(PS,kulcs,érték)-megnöveli
az adott kulcsú elem prioritását az adott értékkel, ha nincs ilyen elem, adjon
hibaüzentet. Növelés után a sor karbantartását el kell végezni (rendezettséget
helyreállítani)!
megoldás
-
Kupaccal ábrázoltunk egy maximum prioritásos sort. Kezdetben a sor üres volt.
A megadott sorrendben beszúrtuk a következő értékeket. Hogyan alakult a kupac
az egyes beszúrások után?
20, 10, 30, 25, 5, 11, 45, 32,
2, 23, 60
-
Kupaccal ábrázoltunk egy maximum prioritásos sort. A kupacot
a tanult módon, egy 12 hosszúságú tömbben helyeztük el. A tömb pillanatnyi
tartalma:
[62 | 46 | 51 | 24 | 22 |
33 | 19 | 7 | 9 | 16 |
8 | ]
Hajtsuk végre háromszor egymás után a maxKivesz() függvényt. Mutassa be, hogyan
változott a kupac az egyes kivételek után. Adja meg fával ábrázolt módon,
illetve a tömbben is kövesse a változásokat. (A tömb három állapotát kell csak
megadni, azt amikor a maxKivesz() már végrehajtódott.)
-
Mutassa be a kupacrendezés iteratív algoritmusának működését a következő tömbön.
Rajzolja le, hogyan alakítja ki az algoritmus a kupac adatszerkezetet,
majd mutassa be az első 2 elem helyrekerülésének, lépéseit.
[ 5 | 8 | 9 | 16 | 7
| 6 | 4 | 18 | 10 | 2
| 14 | 3 | 21 ]
megoldás
-
Mutassa be a kupacrendezés iteratív algoritmusának működését a következő tömbön.
Rajzolja le, hogyan alakítja ki az algoritmus a kupac adatszerkezetet,
majd mutassa be az első 2 elem helyrekerülésének, lépéseit.
[ 2 | 6 | 9 | 5 | 3
| 15 | 14 | 17 | 9 | 12
| 4 | 26 | 11 ]


