Tömbök ábrázolása, hiányos mátrixok helytakarékos ábrázolása

1. Adjuk meg az A[1..m, 1..n] mátrix cím- és indexfüggvényét sor- és oszlopfolytonos elhelyezés mellett is.
   


2. Adjuk meg az A[1..n₁, 1..n₂, 1..n₃] tömb cím- és indexfüggvényét sor- és oszlopfolytonos elhelyezés mellett is.
   


3. Adjuk meg a k dimenziós tömb: A[1..n₁, 1..n₂,..., 1..n_k] cím- és indexfüggvényét sor- és oszlopfolytonos elhelyezés mellett is. Adjunk hatékony (minél kevesebb szorzást használó) módszert az cím kiszámolására.
   


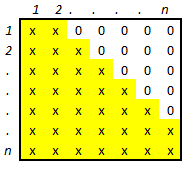
4. Adjuk meg a felső háromszög-mátrix szekvenciális elhelyezésének az indexfüggvényét. Az A[1..n, 1..n] mátrix felső háromszögét a főátló és a főátló feletti elemek alkotják. Ha tudjuk, hogy csak itt lehetnek nullától különböző elemek, akkor elegendő csak ezt a részt, valamint a nulla egy példányát tárolni. Helyezzük el oszlopfolytonosan egy vektorban a felső háromszögbe tartozó elemeket. Mekkora vektorra lesz szükségünk? Mi az összefüggés a sor és oszlop index között, amikor a felső háromszögben vagyunk, azaz az elem tárolva van, és mi akkor, amikor biztosan 0 az érték, tehát nem szükséges tárolni? Adjuk meg az indexfüggvényt. Indexfüggvénynek nevezzük azt a függvényt, mely a sor és oszlop index ismeretében megadja a tárolás szerinti indexét az adott mátrix elemnek. Vizsgáljuk meg azt is, hogyan nézne ki sorfolytonos elhelyezés mellett az index függvény?
   

   megoldás



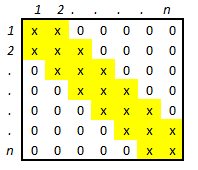
5. A tridiagonális mátrix egy olyan négyzetes mátrix, amelynek a főátlójában és közvetlenül a felett és az alatt (vele párhuzamosan, ferdén) találhatunk nullától különböző elemeket. Milyen indexfüggvény írja le ezeknek az elemeknek (valamint egy példányban a nulla elemnek) az elhelyezését? Mekkora méretű tömbre lesz szükségünk? Mi az összefüggés a sor és oszlop indexek között, amikor a mátrix eleme tárolva van?
   

   megoldás

   
   


6. Írjuk fel az alsó Hessenberg-mátrix indexfüggvényét. Ez az alsó háromszög mátrixhoz képest még egy átlószerű ferde sort tartalmaz, közvetlenül a főátló fölött. Mekkora méretű tömbre lesz szükségünk? Mi az összefüggés a sor és oszlop indexek között, amikor a mátrix eleme tárolva van?
   

   megoldás

   
   


7. A "sakktábla" mátrix egy m x n -es mátrix, melyben a nulla értékű és nem nulla értékű elemek felvátva helyezkednek el: A[1..m, 1..n]. A páratlan sorszámú sorok nem nulla elemmel kezdődőnek, a páros sorszámú sorok nullával. Készítse el a sorfolytonos elhelyezésnek megfelelő index függvényt. Ügyeljen arra, hogy nem mindegy, hogy az oszlopok száma páros vagy páratlan! Próbáljon egységes megoldást találni. Mekkora méretű tömbre lesz szükségünk? Mi az összefüggés a sor és oszlop indexek között, amikor a mátrix eleme tárolva van?
   


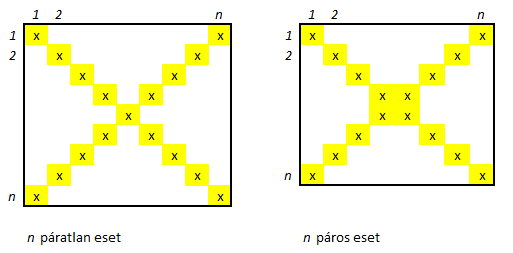
8. "X" alakú négyzetes mátrix. A főátlóban és a mellékátlóban lehetnek nem nulla elemek. Dolgozzuk ki az előbbi feladatokban leírtakhoz hasonlóan a mátrix tárolását n páratlan és n páros esetben is.
   
   


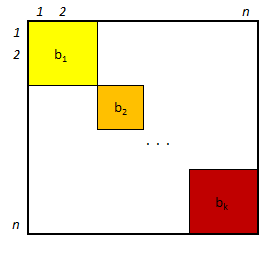
9. Blokkokból álló négyzetes mátrix. A mátrixban a főátlón elhelyzkedő négyzet alakú blokkokban lehetnek nullától különböző elemek. A blokkok átlói illeszkednek a mátrix főátlójára. Dolgozzuk ki az előbbi feladatokban leíratkhoz hasonlóan a mátrix helytakarékos ábrázolását.
   (Tipp: az indexfüggvényt megadhatjuk struktogram formájában is. Tegyük fel, hogy a blokkok mérete egy B[1..k] tömbben van megadva.)