Verem, lengyel forma

Verem létrehozása, használata algoritmusokban
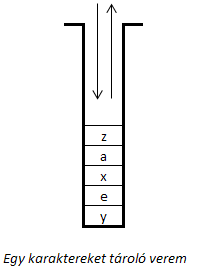	V : Verem	Egy "V" nevű verem létrehozása
	fv V.üres_e()	Logikai függvény, igazat ad, ha üres a verem, hamisat ha nem.
	V.verembe(x)	Az x-ben kapott elemet beteszi a verembe. Bizonyos implementációkban meg kell előtte vizsgálni, hogy a verem tele van-e.
	fv V.veremből()	Kiveszi a veremből a verem tetjén lévő elemet, és visszatérési értékként átadja. CSAK nem üres veremre használható.
	fv V.tető()	A verem tetején lévő elemet visszatérési értékként átadja. Nem veszi ki a veremből a megvizsgált elemet. Csak nem üres veremre használható.
	fv V.tele_e()	Logikai függvény, igazat ad, ha tele van a verem. Nincs mindig implementálva, általában a verem tud "nyújtozkodni", ha elfogyott a memória hely. Így az algoritmusokban nem szoktuk használni.
	V.üresVerem()	"Kiüríti" a vermet. Ha nem üres a verem, tartalma elvész.

1. Döntsük el verem használatával egy "(" és ")" karakterekből álló sorozatról, hogy helyes zárójelezés-e.



2. Egy szekvenciális input sorozat a "(" és ")" karakterekből álló helyes zárójelezést tartalmaz. Írjunk olyan, vermet használó eljárást, amely az összetartozó zárójel párok sorszámait egymás sorban mellé írja. Például:
   Bemenet ( ( ( ) ) ( ) ) Kimenet: 3,4,2,5,6,7,1,8.



3. Döntsük el vermes algoritmussal, hogy egy "(,),[,],{,}" zárójeleket tartalmazó kifejezés helyes zárójelezés-e. A zárójelek egymásba ágyazására a következő megszorítások érvényesek:
   • "{ }" -ben lehet : { } vagy [ ] vagy ( )
   • "[ ]" -ben lehet : [ ] vagy ( )
   • "( )" -ben csak újabb ( ) lehet.
   • A kifejezésben szereplő egyéb jeleket egyszerűen csak olvassuk át.
   Csak a zárójeleket kiemelve helyes például: { { ( ) [ ] [ ( ) ] } ( ( ) ) { } }
   Helytelenek: [ { ( ) } ] vagy ( ( [ ] ) ) vagy [ ( ) ( ( ) ] vagy { ] [ } stb.
   megoldás



4. Ellenőrizzük verem (vermek) használatával, hogy az input sorozat palindrom-e. Oda-vissza olvasva ugyanaz. Oldjuk meg a feladatot kétféle képpen is.
   
   • Ismerjük a bemenet hosszát.
   • Nem ismerjük a bemenet hosszát. (Használjunk a megoldásban két vermet.)



5. Adott egy szekvenciális input fájl, mely „egyszerű jeleket” (jelöljük őket betűkkel: a,b,c …) és „(” és „)” zárójeleket tartalmaz. Feltesszük, hogy a zárójelpárok helyesek és nincsenek egymásba ágyazva. Feladat: verem felhasználásával állítsuk a következő kimeneti fájlt: a „(” és „)” zárójelek között az egyszerű jelek sorrendjét megfordítjuk, a zárójeleken kívüli jeleket az eredeti sorrendjükben írjuk ki. A jelsorozat lehet üres, vagy lehet, hogy nem tartalmaz egyetlen zárójelet sem. Például:
   a b c ( d e f ) n g ( h i )( ) j bemenet esetén
   a b c ( f e d ) n g ( i h )( ) j a kimenet
   megoldás



6. Egy szekvenciális input fájlban adott egy jelsorozat. Elemei közül kitüntetett a “*” elem. Készítsen egy olyan eljárást, mely egy verem felhasználásával "*" elemek által elválasztott részsorozatokat fordított sorrendben írja ki, úgy, hogy az egymás mellett álló azonos jelekből csak egyet ír ki a kimentre. A bejövő jelsorozatot csak egyszer olvashatjuk végig. A sorozat elején és végén nem kötelező "*" jelnek állnia, de ezeket is részsorozatnak tekintjük. Példák (bemenet :® kimenet):
   abcc*s**gge ® cba*s**eg
   *fffafffb* ® *bfaf*
   megoldás



7. Adott egy jelsorozat, az elemeket jelölje A, B, C, D, ... Van egy speciális jel a #. Verem segítségével alakítsuk át a sorozatunkat úgy, hogy a # jelekre szimmetrikus legyen: a # jel előtt álló jeleket fordított sorrendben ismételjük meg a # jel után.
   Például:
   A B # C # D E       →     A B # B A C # C D E # E D
   
   
8. Az S szekvenciális input sorozat neveket tartalmaz vesszővel elválasztva. A nevek névsorba rendezettek, az utolsó név után egy # jel áll. Készítsünk olyan vermes algoritmust, amely fordított névsorban írja ki a neveket. Az olvasás és írás egysége a karakter.
   Például:
   ANNA, GÁBOR,PÉTER,VERA#   →  VERA,PÉTER,GÁBOR,ANNA#
   
   
9. Létezik-e olyan 10-es számrendszerben felírt n>0 számjegyű természetes szám, amelyre teljesül, hogy a számjegyeiből alkotott sorozat bármely nullánál hosszabb prefixének számjegyeinek az összege osztója a prefixnek, mint 10-es számrendszerben felírt számnak? Pl.: 126 szám ilyen, mert prefixei: 1, 12, 126 és 1|1, 1+2|12 és 1+2+6|126. Ha létezik az említett tulajdonságú szám, akkor adjuk meg a legnagyobb ilyet. A feladatot oldjuk meg vermet használó algoritmussal.

Lengyel forma és a lengyel formára hozás algoritmusa

Egy részletesen kidolgozott feladat

1. Hozzuk lengyel formára az alábbi kifejezést. A lengyel formában az operandusok felett ábrázoljuk a verem pillanatnyi tartalmát:
   y = z = a ^ 2 + x / ( 5 - e * ( a ^ 3 ^ k / l - f ) ) - d
   megoldás
   


2. Hozzuk lengyel formára az alábbi kifejezést. A kifejezésben találhatók mínusz előjel operátorokat soroljuk be a műveleti jelek rangsorába. A lengyel formában az operandusok felett ábrázoljuk a verem pillanatnyi tartalmát:
   y = c - ( a / − b ^ k ^ 3 - ( h - z ^ 2 / − g ) + i ) / j ^ 2 * x + w
   


3. Adott egy teljesen és helyesen zárójelezett kifejezés. Készítsünk algoritmust, mely verem használatával a kifejezést egyszer végig olvasva előállítja a kifejezés lengyel formáját.
   


4. Adott egy aritmetikai kifejezés lengyel formája. Készítsünk algoritmust, mely a lengyel formát végig olvasva előállítja a kifejezés teljesen zárójelezett alakját.