Sorbaállítás (Számítógépes hálózat építés)

A számítógépes hálózatok tervezése során a számítógépeket össze kell kötni egymással. Az így létrejövő hálózat lineáris felépítésű, azaz bármely számítógép pontosan két másikhoz kapcsolódik, kivéve a lánc elején és végén lévő számítógépeket, amelyek csak egy számítógéphez kapcsolódnak. Egy ilyen hálózatot mutat az alábbi ábra, amelyen a számítógépeket fekete pontok jelölik. A számítógép helyzetét síkbeli koordinátákkal írjuk le (a koordinátarendszer nincs feltüntetve az ábrán). A csatlakozó gépek közti távolságot lábban mérjük.

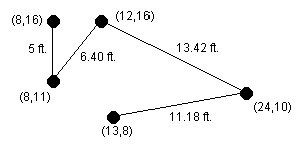
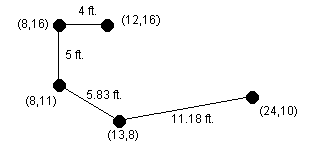
Különböző okokból kívánatos, hogy minimalizáljuk az elhasznált kábel hosszát. Írjunk programot, amely meghatározza, hogy milyen sorrendben kell a gépeket összekötni ahhoz, hogy az elhasznált kábel hossza minimális legyen! A kábelek a föld alatt húzódnak, ezért két szomszédos gép összekapcsolásához szükséges kábel hossza 16 lábbal több, mint a két gép távolsága. Az alábbi képen a fenti hálózat egy optimális kapcsolása látható; a konfigurációhoz szükséges kábelhossz (4+16) + (5+16) + (5,83+16) + (11,18+16)=90,01 láb.

Bemenet:

Az input fájl több adatsort is tartalmazhat. Minden adatsor első sora a hálózatban lévő gépek számát tartalmazza. Egy hálózatban legalább 2, legfeljebb 8 gép van. Ha a hálózatban szereplő gépek száma 0, akkor az, az input végét jelöli. A számítógépek számát definiáló sor után következő sorok a hálózatban lévő gépek koordinátáit tartalmazzák. A koordináták egész számok a [0..150] intervallumból. Minden számítógép egyszer van listázva, és bármely pontban legfeljebb egy számítógép van.

Kimenet:

Az outputnak minden hálózatra tartalmaznia kell annak sorszámát (melyet az inputban elfoglalt pozíciója határoz meg), valamint minden egyes kábel darabra egy sort, amely tartalmazza a kábel hosszát, és az összekötött számítógépek koordinátáit! A hálózathoz tartozó utolsó sor a minimálisan szükséges kábel összes hosszát tartalmazza! A kábel darabok listázásánál sorba haladjunk a hálózat egyik végétől a másikig! Kövessük a példa outputban bemutatott formátumot! Az egyes adatsorokhoz tartozó eredményeket, egy csillagokat tartalmazó sorral válasszuk el! A távolságokat két tizedes jegyre kerekítsük!

Példa:

INPUT.TXT

OUTPUT

6 5 19 55 28 38 101 28 62 111 84 43 116 5 11 27 84 99 142 81 88 30 95 38 3 132 73 49 86 72 111 0

********************************************************** Hálózat #1 A(z) (5,19) és (55,28) összekötéséhez szükséges kábel hossza: 66,80 láb. A(z) (55,28) és (28,62) összekötéséhez szükséges kábel hossza: 59,42 láb. A(z) (28,62) és (38,101) összekötéséhez szükséges kábel hossza: 56,26 láb. A(z) (38,101) és (43,116) összekötéséhez szükséges kábel hossza: 31,81 láb. A(z) (43,116) és (111,84) összekötéséhez szükséges kábel hossza: 91,15 láb. A szükséges kábel hossza: 305,45 láb. ********************************************************** Hálózat #2 A(z) (11,27) és (88,30) összekötéséhez szükséges kábel hossza: 93,06 láb. A(z) (88,30) és (95,38) összekötéséhez szükséges kábel hossza: 26,63 láb. A(z) (95,38) és (84,99) összekötéséhez szükséges kábel hossza: 77,98 láb. A(z) (84,99) és (142,81) összekötéséhez szükséges kábel hossza: 76,73 láb. A szükséges kábel hossza: 274,40 láb. ********************************************************** Hálózat #3 A(z) (132,73) és (72,111) összekötéséhez szükséges kábel hossza: 87,02 láb. A(z) (72,111) és (49,86) összekötéséhez szükséges kábel hossza: 49,97 láb. A szükséges kábel hossza: 136,99 láb.

(ACM döntő 1992)