Kristálytiszta

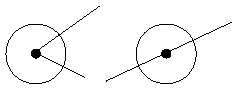
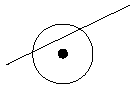
Egy csúcstechnológiával dolgozó cég előállított egy új anyagot, amelyet mint szigetelőt szeretne piacra dobni. Az anyag négyzetes rácsszerkezetben növekvő kristály. A rácsszerkezet cellái 1 centiméterenként helyezkednek el. Minden cella pontosan 1 centiméter átmérőjűre nő. Az anyag felhasználásához a kristályrács darabolása szükséges. A rács darabolása során jelentkező egyik probléma, hogy néhány cellába is belemetszünk. Ha egy cellát nem a közepénél vágunk el, elveszíti szigetelő tulajdonságát.

megmarad a szigetelőképesség	elvész a szigetelőképesség

A rácsszerkezet szigetelőképessége egyenesen arányos a szigetelő tulajdonságú kristályok (vagy kristályrészek) teljes területével. A következő ábra egy sokszög alakú rácsrészt mutat, amelyen árnyékoltan láthatók a szigetelő kristályok.

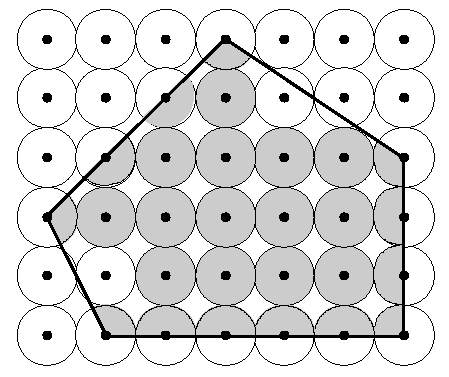
A feladatod, hogy határozd meg a szigetelőképességet a szürkével jelzett terület kiszámításával.

Bemenet:

A bemeneti állomány tartalmazza a sokszög leírását. Minden leírás egy n pozitív egésszel kezdődik (3 <= n <= 25), megadja a csúcsok számát. A következő n egész számpár a csúcsok x és y koordinátáját adja meg. (A koordinátarendszert úgy helyeztük el, hogy a cellák középpontjai egész koordinátájúak legyenek.) A csúcsok az óramutató járásának sorrendjében adottak. A sokszög konvex. A csúcspontok egyik koordinátája sem nagyobb abszolút értékű, mint 250. A bemeneti állományt a 0 érték zárja.

Kimenet:

A kimenetbe tesztesetenként az eset sorszámát kell írni, a következő sorba a szigetelő tulajdonságú terület méretét kell írni 3 tizedesjegy pontossággal.

Példa:

INPUT.TXT	OUTPUT.TXT
5 0 2 3 5 6 3 6 0 1 0 0	1. eset szigetelo terulet = 15.315 cm^2

(ACM döntő 1998)