A számítógépes szimulációt matematikai szempontból két oldalról kívánjuk megközelíteni. Egyrészt a determinisztikus gép „véletlen generálási” lehetőségeit, módjait vizsgáljuk, amivel a számítógép ezen önmagában véve paradoxnak tűnő „képessége” körül oszlatjuk el a ködöt. Másrészt megtanuljuk a számítógép adta véletlenszámok sorozatát természetutánzásra használni, miközben érthetővé válik, hogy milyen alapon várhatunk el a szimulációs modellünktől, egy véletlen irányította modelltől objektív, a modellezettről „igazakat” állító eredményeket.
A számítógép produkálta véletlenről – úgy gondoljuk – nem eshet szó addig, amíg a véletlen „természetét”, a véletlentől elvárt tulajdonságokat nem tisztáztuk.
A. A véletlenszerű kísérletektől elvárjuk, hogy minden lehetséges kimenetele előbb-utóbb bekövetkezzék.
B. Az eseményre vonatkozó kísérleteinket jellemezze az is, hogy addigi bekövetkezésekből (vagy be nem következésekből) ne következtethessünk a továbbiak kimeneteleire. (Azaz legyenek egymástól függetlenek.)
C. E két kvalitatív elvárásunkat pontosíthatjuk az alábbi kvantitatív állításunkkal: a szimulációnk akkor valósághű, ha a szimulált kísérletek kimeneteleinek relatív gyakorisága kifejezi a hozzátartozó valóságos események valószínűségeit. (Azaz a nem nulla valószínűségű esemény relatív gyakorisága nem nulla, pontosabban akkora, mint maga a valószínűség. Másrészt két vagy több kísérletünk kimeneteleinek együttes relatív gyakorisága egyezzék meg ezek együttes bekövetkezésének valószínűségével.)
(Számítógépről lévén szó azon semmi csodálkozni való nincs, hogy egy számalgoritmust keresünk, amely véletlen események gyanánt véletlenszámot eredményez.)
Kérdés tehát, hogy lehet-e olyan determinisztikus algoritmust konstruálni, amely a fentieket teljesíti? Az igenlő választ történetileg először Neumann János adta meg: a négyzetközép-nek elnevezett módszerével. A lényege a következő:
Induljunk ki egy 2*k jegyű számból! Emeljük négyzetre, majd az így keletkezett 4*k jegyű szám középső 2*k jegyét tekintsük az első véletlenszámnak (itt a véletlen esemény maga a szám kijötte)! Ebből a számból állítjuk elő a fenti módon a másodikat, és így tovább ...
A négyzetközép módszer egy variánsát – a szorzatközép módszert – az alábbi algoritmus valósítja meg! Állítsunk elő kétjegyű álvéletlenszámokat, a kiinduló értéket olvassa be a program! (A négyzetre emelés művelet szerepét töltse be az A*előző szám+B formula!)
Program:
Be: R0; A:=11; B:=53
Ciklus amíg szükséges
Ki: R0
R:=(R0*A+B) div 10 [R = a szorzat utolsó jegye nélkül]
R0:=R mod 100 [R0= a szorzat középső két jegye]
Ciklus vége
Program vége.
Ha R0-nak például a 32 kezdőértéket adjuk, az alábbi sorozatot kapjuk:
40, 49, 59, 70, 82, 95, 9, 15, 21, 28, 36, 44, 53, 63, 74, 86, 99, 14, 20, 27, 35, 43, 52, 62, 73, 85, 98, 13, 19, 26, 33, 41, 50, 60, 71, 83, 96, 10, 16, 22, 29, 37, 46, 55, 65, 76, 88, 2, 7, 13, ...
Célszerű több kezdőérték mellett (sőt más A és B esetére) is álvéletlenszám-sorozatokat generálni! Vegyük észre a módszer jellegzetességeit, hibáit!
1. Gyakoriak az olyan kezdőértékek (R0,A,B), amelyekre nagyon rosszul viselkedik: elfajul a sorozat. (Például állandóan ugyanazt az egy értéket szolgáltatja.)
2. Észrevehetően periodikus, ami a determinisztikusságból fakad. (Elvileg sem tudna 100-nál hosszabb periódusú sorozatokat produkálni, hiszen kétjegyű szám csak 100 van, ugyanabból a számból generálva másodszor is csak ugyanúgy folytathatja, azaz az ismétlődés garantált.)
3. A kapott álvéletlenszám-sorozatokat az alábbi szakaszokra lehet bontani:
[aperiodikus szakasz] [periodikus szakasz] [periodikus szakasz]
Ebből következik, hogy nem célszerű az aperiodikus szakasz hosszánál több véletlenszámot generálni!
4. Aprólékosabban elemezve a kapott sorozatot újabb kellemetlen sajátosságokat fedezhetünk föl. Például hosszabb, növekvő (méghozzá sajnálatosan elég szisztematikusan növekvő!) szakaszok ismétlődését tapasztalhatjuk.
A módszer mindezen, túlontúl „átlátszó” hibái az eljárás lényegéből fakadnak, mégis megemlítettük történeti érdekessége és egyszerű megvalósíthatósága miatt.
Állítás: Ha m=2k, a=4*x+1, (c,m)=1 (és m prímosztói a–1-nek is prímosztói) , akkor m lesz a periódushossz.
Megjósolhatóság kérdése:
A gyakorlatban használatos véletlenszám-generátorok többsége a lineáris kongruencia módszer speciális esete:
Adott k+1 db egész szám (a0,a1,...,ak), ezek a kongruencia együtthatói, és k db (R0,R1,...,Rk-1) kezdőérték. Az Rn+1-t az előzőkből az Rn+1≡a0*Rn+a1*Rn-1+ ... +ak-1*Rn-k+1+ak (mod M) formula alapján számoljuk.
Ennek kiszámolásáról csak annyit, hogy a következő véletlenszám a ≡-jel jobboldalán levő kifejezés értékének M-mel való osztási maradéka. Az M modulus és az együtthatók alkalmas választásával megközelíthető a periódus elvi korlátja (Mk).
Az egyes konkrét véletlenszám-generátorokhoz kiszámolható a periódus. Hogy némi fogalmunk legyen ennek nagyságrendjéről, közöljük, hogy például egy Rn+1≡(10a+1)*Rn+Rn-1 (mod 10b) formulával definiált véletlenszám-generátor periódushosszát az 1.5*10b képlettel határozhatjuk meg.
A véletlenszám-előállító algoritmusok további példájaként egy érdekes módszert említünk. A kongruencia módszerből M=2 és az első együttható=1 esetén kapjuk. A továbbiakban az együtthatók is, a véletlenszámok is a 0 vagy az 1 értékek valamelyikét vehetik föl. Úgy értelmezhetjük a módszert, mintha a számokat „bitenként” véletlenül generálná. Az érdekessége az, hogy meglepően jó a periodicitás szempontjából: 2k-1. (A k a következő bit előállításában résztvevő bitek száma.) Ha m bináris jegy alkotja a véletlenszámunkat, akkor a következőt az előző m-1 db, valamint az újonnan generált véletlen bit alkotja. Ily módon éppen 2k ilyen szám létezik, tehát csak eggyel több, mint a periódus hossza. (Melyik szám lehet az, amit nem generál?) Továbbiakban jelöljük P-vel a periódus hosszát!
Könnyen beláthatók a módszer és a P ismeretében az alábbi, a használhatóságot jelentő állítások.
1. Ha egy kezdő k bit-variációra P=2k-1 periódushosszú sorozatot ad, akkor tetszőlegesből indítva (kivéve a csupa 0-ból állót) a periódus hossza továbbra is ugyanazon P marad. (Hiszen a k db 0-t tartalmazó szakaszt kivéve az összes bit-k-ast generálja.)
2. Az aperiodikus szakasz hossza is P.
3. Az m (<k+1) bites bit-variációk száma 2k-m, a csak 0-t tartalmazó m-esek száma pedig eggyel kevesebb. Ennek következménye, hogy „majdnem” egyenletes eloszlást követ.
Persze ez utóbbi módszer ritka példája annak, hogy a véletlenszám generátornak elvileg határozhatjuk meg az egyes számvariációk „eloszlását”. S ezzel bizonyíthatjuk jóságát vagy éppen használhatatlanságát. A gyakorlatban nem ilyen kedvező az ellenőrizhetőség helyzete. Általában mintasorozatokat generálva készítenek statisztikákat, s mint egy valódi véletlenfolyam tulajdonságaira ily módon következtetnek.
Egy kis kitérő: Vajon melyek a „jóság” legfontosabb kritériumai?
Vegyünk egy vi (i=1,...) véletlenszám sorozatot!
Mivel minden K-ra nem tudjuk megnézni, más lehetőségeket kell választanunk:
Az utóbbi módszer elvi alapját Weyl-től származó alábbi tétel alkotja:
Annak, hogy az n-dimenziós kockában véletlenszerűen elhelyezett pontsorozat egyenletes eloszlású legyen, szükséges és elégséges feltétele, hogy bármely T tartomány esetén
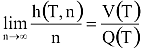
ahol Q(T) a teljes kocka térfogatát, H(T,n) a T-be esés relatív gyakoriságát, V(T) pedig a T térfogatát jelöli.
A K-számjegy-kombinációk gyakoriságát számláló algoritmus az alábbi! Gyak(i) -ben számláljuk az i. kombináció gyakoriságát, a Szám() vektorban tároljuk a következő K véletlen számjegyet.
Program:
Be: N,K [N>0: a kísérletek száma, K>0: számjegy kombinációk hossza]
L := ismétlés-kombináció(10,K)
Ciklus i=1-től N-ig
K_véletlen_számjegy(Szám)
[a következő K véletlen számjegy előállítása a Szám-ban]
j:=Kombináció_index(Szám)
[valamilyen, rögzített rendszer szerinti sorszáma a Szám kombinációnak]
Gyak(j):=Gyak(j)+1
Ciklus vége
Gyakoriságmegjelenítés(Gyak)
Program vége.
A program kifejtésébe most nem bonyolódunk. Az Olvasónak maradjon gyakorlásként a „specifikált” eljárások részletezése!
A véletlenszám-generátorok egyfajta javítási lehetőségével ismerkedünk meg a téma lezárásaként:
Adott két (esetleg több) P1, P2 (...) periódushosszú generátor. A két (több) generátor egy (valamilyen „topológiájú”) integrált rendszerben állítja elő a véletlenszámokat. Ennek topológiája szerint a következő felosztásban csoportosíthatjuk a véletlenszám-generátorokat:
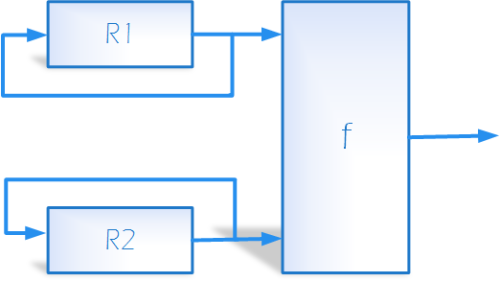 Két generátor párhuzamos kapcsolása.
Két generátor párhuzamos kapcsolása.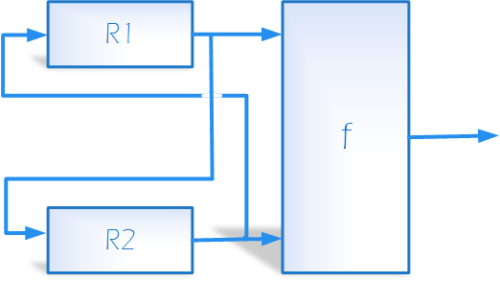 Két generátor visszacsatolásos kapcsolása.
Két generátor visszacsatolásos kapcsolása. Két generátor soros kapcsolása.
Két generátor soros kapcsolása.Sejthető, hogy ezen kombinált módszerrel kapott véletlen-sorozat általában kedvezőbb lesz periodicitási (periódushossz és stabilitás – kezdőértéktől való kisebb függés) és statisztikus szempontokból, de nem jár a megvalósító program lényeges bonyolításával. (Megjegyezzük, hogy a módszerrel óvatosan kell bánni, néha váratlanul rossz sorozatot eredményez.)
A szorzatközép módszerre megírt programot felhasználva adjuk meg két különböző A, B paraméterrel működő generátor „összefésülésének” algoritmusát!
Program:
Be: R0(1),R0(2) [a két generátor kezdőértékei]
A(1):=11; B(1):=53; A(2):=13; B(2):=51
[a generátorokat meghatározó paraméterek beállítása]
i:=1
[az „első” generátor adja az első véletlen értéket]
Ciklus amíg szükséges
A:=A(i); B:=B(i); R0:=R0(i)
Ki: R0[A,B= az aktuális generátor paraméterei]
R0:=Szorzat_közép(R0,A,B)
i:=3-i[i= a másik generátor indexe]
Ciklus vége
Program vége.
Szorzat_közép(R0,A,B):
R:=(R0*A+B) div 10 [R = a szorzat utolsó jegye nélkül]
Szorzat_közép:=R mod 100 [R0= a szorzat középső két jegye]
Függvény vége.
A véletlenszámokkal szemben támasztott „heurisztikus” követelményeink közül a másodikra (B) térjünk vissza még egy, talán meglepőnek tűnő gondolattal! Sokszor még az sem lényeges, hogy legalább „látszólag” megjósolhatatlanul kövessék egymást a véletlenszámok. Olyan esetekre kell gondolnunk, amelyeknél a szimulációs folyamat „egyszerű” struktúrájú. Ilyenkor bármely olyan számsorozat jó, amelyben minden szükséges variáció az elméletileg elvárt gyakorisággal fordul elő. Az előfordulásuk sorrendje lényegtelen! Akár növekvően rendezve is adhatók.
Célszerű persze a kísérletek számát a számsorozat hosszának többszörösére választani.
1. példa: ha 1 és 9 közötti véletlenszámokra van szükségünk (és a szimulált rendszer a fenti tulajdonságú), akkor a következő sorozat is megfelelő:
1 , 2 ,..., 9 , 1 , 1 , 1 , 2 , 1 , 3 ,..., 1 , 9 , 2 , 1 ,..
A folytatás – úgy gondoljuk – mindenki számára világos. Próbálja a fenti sorozatot program segítségével generálni! A sorozat felhasználásáról csak annyit, hogy abbahagyni „10k-1 felbontásánál” (valamely k-ra) szabad. (Ugyanis ekkor garantálható legalább a számjegyek azonos gyakorisága!).
2. példa: ha egy k dimenziós valószínűségi vektorváltozót használunk föl a szimuláció során, akkor k-ad rendig bezárólag kell egyenletesen szerepeltetni a variációkat, így:
1, 1,..., 1, 1, 1, 1,..., 2, 1, 9, 9,..., 9, 1,
1, 1,..., 1, 2, 1, 1,..., 2, 2, 9, 9,..., 9, 2,
... ... ...
1, 1,..., 1, 9, 1, 1,..., 2, 9, 9, 9,..., 9, 9.
A számítógépes szimuláció elvi „jóságának” indoklását a sztochasztikus folyamatokkal való kézenfekvő kapcsolata segítségével építjük föl.
A kapcsolat elvi alapjait négy aspektusból fogjuk áttekinteni.
A. A szimuláció és a szimulálandó elvi azonosságát, mint folyamatok azonosságát vizsgáljuk.
B. Látni fogjuk, hogy a szimulációs folyamatot a szimuláció közben „állóképek” sorozatából rakhatjuk össze. Csak ezen pillanatfelvételek jóságát kell biztosítanunk. Ehhez annak vizsgálata szükséges, hogy a folyamat adott, rögzített időpontbeli állapoteloszlását miként tudjuk valósághűen visszatükrözni.
C. Az elvi alapok taglalását a szimuláció „módszertani” alapjául szolgáló Glivenko-tétellel folytatjuk.
D. Végül egy a szimuláció praktikus vetülete felé átvezető problémát vetünk föl: meddig kell folytatnunk a kísérletet, hogy „megnyugtatónak” érezhessük az eredményeinket.
Az elméleti alapok ismertetése után rátérünk a számítógépes szimuláció gyakorlati kérdéseire (a 3.3. pontban). Itt a számítógép véges pontosságából adódó hiba vizsgálatával kezdjük a gyakorlati problémák sorát, majd számos programozástechnikai részlettel, fogással folytatjuk.
Írja le a szimulálandó folyamatot az X(t), a szimulációs folyamatot az Y(t) valószínűségi változó. A szimulációt akkor tekinthetjük jónak, ha a szimulálandó és a szimulációs folyamat (bármely t időpillanatában) egy tetszőlegesen választott állapotában azonos valószínűséggel tartózkodik.
Azaz, P(X(t)=s)=P(Y(t)=s), feltéve, hogy az „indulás” körülményei azonosak voltak: P(X(0)=r)=P(Y(0)=r), ahol r és s tetszőleges folyamatbeli állapot. Igaz a következő állítás:
A P(X(t)=s)=P(Y(t)=s) teljesülésének szükséges és elégséges feltétele, hogy a P(X(t)=s|∀u<t: X(u)∈Γ) = P(Y(t)=s|∀u<t: Y(u)∈Γ) ∀s állapotra. Itt a Γ a folyamat pályáját jelöli.
Az állítás jelentése a következő: sztochasztikus értelemben a szimulációs folyamat akkor és csak akkor ekvivalens a szimulálandóval, ha a szimuláció során az állapotváltozás valószínűségi szempontból azonos a szimulálandóéval, figyelembe véve a folyamat eddig befutott pályáját. Tehát a folyamat teljes ismerete helyett (hiszen általában ennek megismerése a cél) elegendő a kezdeti állapoteloszlás valamint az állapotváltozás módjának ismerete, ami a legrosszabb esetben is a teljes eddigi pálya figyelembe vételét jelenti. A konkrét esetekben látni fogjuk, hogy nagyon sokszor ennél jóval kevesebb információval is meghatározható a továbblépés eloszlása.
A matematikai analízisből vett példával élve hasonló a helyzet, mint amikor egy függvényt kell „rekonstruálni” a változás (derivált) függvény segítségével. Érdemes eltöprengeni az analógián!
Figyelmünket most a folyamat egy adott, rögzített időpontbeli „pillanatképére” fordítjuk. Induljunk ki abból a feltevésből, hogy rendelkezünk a szimulációhoz egy F eloszlást követő X valószínűségi változóval. Kérdés, hogyan állíthatunk elő ebből más eloszlású valószínűségi változókat? Erre egy direkt formulával válaszolunk, amely alkalmazására később számos példát látunk. Ha a G eloszlású Y valószínűségi változót kell szimulálnunk, akkor az X-et transzformálnunk kell, mégpedig a G-1(F(X)) formula segítségével. (Itt a G-1 a G inverzét jelöli!)
E transzformáció jogosságának belátására csak az eloszlás fogalmához kell visszanyúlnunk:
P(Y<x)=P(G-1(F(X))<x)=P(F(X)<G(x))=P(X<F-1(G(x)))=F(F-1(G(x)))=G(x).
E direkt formula használatára most csak két példát említünk.
Tegyük föl, hogy az X E[0,1) (azaz a [0,1) balról zárt jobbról nyílt intervallumban egyenletes) eloszlást követ, s szeretnénk az Y E[a,b)-belit segítségével előállítani. A direkt módszer szerint nincs más teendőnk, mint megkeresni a G(x)=P(Y<x) függvény inverzét. Tudva, hogy a G(x)=(x-a)/(b-a), az inverzére a G-1(x)=x*(b-a)+a adódik.
Ugyanis G-1(G(x))=G-1( (x-a)/(b-a) )=x , amit teljesítenie kellett.
Második példaként az előbbi X-ből „származtassunk” egy Y m-paraméterű exponenciális eloszlású valószínűségi változót!
Az Y eloszlásfüggvénye: G(x)=1-e-m*x.
Keressük azt a G-1 függvényt, amelyre igaz a G-1(G(x))=x ∀x-re, azaz G-1(1-e-m*x)=x.
Kérdés, hogy az 1-e-m*x-ből milyen transzformációval „hozható ki” az x?
Ránézésre adódik:
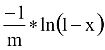
Mivel 1-x eloszlása ugyanaz, mint az x-é, ezért igaz az (egyszerűbb) formula:
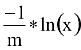
Ezen az ún. direkt módszeren kívül több más módszer is ismert. Egy-kettőre az alkalmazások során ki is térünk.
1.-ben a folyamatot „állóképekre” bontottuk úgy, hogy a következő képet a folyamat változása determinálja. A 2.-ban megmutatott módon e változást valószerűvé tudtuk tenni, bármilyen eloszlást is kövessen az. Most megmutatjuk, hogy a szimulációs eljárásunk „filozófiája” – ti. hogy adott eloszlás szerint egyedi véletlen eseményeket generálunk, s ezek együttesen alakítják ki a valóságos képet – helyes. Ha ugyanis az adott eloszlás szerint generált eseményeket számláljuk, és képezzük ezek relatív gyakoriságát (pontosabban az empírikus eloszlást), akkor a kísérletek (esemény-generálások) számát növelve egyre jobb az egyezés az empírikus és az elméleti eloszlás között (ezt fejezi ki a Glivenko-tétel).
A tétel súlyát és „kényszerítő erejét” lássuk be oly módon, hogy számoljuk ki rögzített ε (ε>0) esetén mi a valószínűsége a
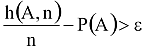
eseménynek egyre növekvő n-re. (Itt h(A,n) az A esemény gyakoriságát jelenti n kísérlet után, a P(A) az A valószínűsége.)
A szimuláció során nem kísérletezhetünk végtelenségig. Egyrészt időkorlát miatt, másrészt a számítógép véges pontossága miatt sincs értelme bizonyos határon túl a kísérletek számát növelni. Van-e arra vonatkozó információnk, hogy meddig érdemes a kísérleteket végezni? A válasz igenlő, de ahogy már megszoktuk, valószínűségi jellegű. Ugyanis szimulációnál csak valamilyen valószínűséggel tudunk bármit is „garantálni”. Az előírt pontosságú közelítéshez szükséges kísérletek számát legegyszerűbben a Csebisev tétel alapján konstruálhatjuk meg:
Meghatározandó a kísérletek azon száma (n), amelyre a pontosság, 1-p a megbízhatóság:
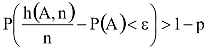
A Csebisev tételt alkalmazva kapjuk:
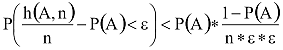
Innen a feltétel kielégíthető, ha
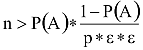
Tegyük föl, hogy addig kísérletezünk, ameddig a kedvező esetek száma eléri az m-t: h(A,n)=m, ekkor a
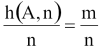
érdekel bennünket!
véletlenszám generátorunk – feltevésünk szerint – [0,1) egyenletes eloszlást követ. Pontosabban a számítógép véges pontossága miatt ezt helyesebb lenne „diszkrét egyenletes” eloszlásnak nevezni, hiszen ha a pontossága d, akkor a véletlenszámok a következők lesznek: 0, d, 2*d, ..., i*d,..., N*d, ahol N:=1/d-1. Feltesszük, hogy a generátorunk a fenti számokat egyenletesen, azaz azonos d valószínűséggel állítja elő. Továbbá feltesszük, hogy egyéb számolásokra és konstansokra is jellemző a pontosság fenti d értéke.
Pontosság alatt értjük: két megkülönböztethető normalizált szám különbségének abszolút értéke legalább d.
Azt a kérdést kell megválaszolnunk, hogy milyen alapon várunk el a számítógépes szimulációtól a valóságra utaló, a szimulációs folyamatra jellemző adatokat, információkat, illetve hogyan kell egyáltalán komplex jelenségeket szimulálni. Keressük előbb az első kérdésre a választ!
Tekintsük a véletlenszám-generátort valószínűségi változónak (R), amely a valós [0,1) intervallumon van értelmezve és a d[0,1):={i*d: i=0..N} az értékkészlete.
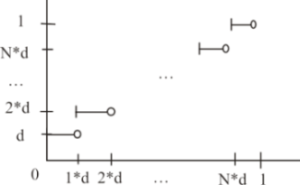 A véletlenszám-generátor, mint függvény, diagramja.
A véletlenszám-generátor, mint függvény, diagramja.Jelöljük R(i)-vel az i.-ként generált véletlenszámot. Ekkor az R(i) sorozat sztochasztikus folyamatot alkot.
Mekkora hibát követünk el akkor, ha eltekintünk a véletlenszám-generátor „diszkrét” voltától? A hibabecslés érdekében számítsuk ki e diszkrét egyenletes eloszlás várható értékét és szórását!
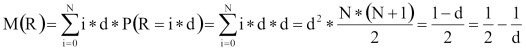
Közben felhasználtuk az N és a d közötti összefüggést, és a diszkrét egyenletességet: P(R = i * d) = d.
Azaz az egyenletestől való eltérés – a várható érték szempontjából – az ábrázolási pontosság felével egyenlő.
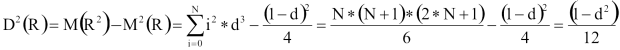
Hasonló következtetésre jutottunk a szórásnégyzetet illetően: a szórásnégyzet a pontosság négyzetének (!) 12-ed részével tér el a (folytonos) egyenletes eloszlású valószínűségi változó szórásnégyzetétől.
Tehát a levonható tanulság: Az eltérés a „valódi” egyenletes eloszlástól nem haladja meg az ábrázolási pontosság értékét, amiből látszik, hogy a bizonytalanság legfeljebb az utolsó jegyben mutatkozhat.
A komplex jelenségek szimulációjának „hogyanját” közelítsük meg a legegyszerűbb alapeset felől! Egy p valószínűségű A eseménnyel kapcsolatos kísérletet kell lejátszanunk. Definiáljunk egy valószínűségi változót, X(A)-t, amely akkor 1, ha az A bekövetkezett, és 0 egyébként (X(A) az A esemény indikátorváltozója). Ennek tehát értelmezési tartománya az {A,-A} halmaz, és értékkészlete a {0,1}.
-A az A esemény komplemensét (kiegészítőjét) jelöli.
Jelölje R (valószínűségi változó) a véletlenszám-generátor adta számsorozat egy elemét! Miként kapcsolhatjuk össze X(A)-t és R-t úgy, hogy azt állíthassuk, hogy e két valószínűségi változó ekvivalens valószínűségi értelemben? A kapcsolatot egy függvény segítségével építjük ki. Első lépésként az R és az X(A) eltérő értelmezési tartományát kell megvizsgálnunk. Osszuk Do(R) pontjait két osztályba, s feleltessük meg az egyik osztályt A-nak, a másikat -A-nak. Definiálunk egy R(A) függvényt úgy, hogy Do(R(A))=Ra(R), Ra(R(A))= {0,1} és R(A)(R(o)):=1, ha az o az A-hoz lett rendelve, és 0, ha az o -A-hoz tartozik.
A továbbiakban Do(f) jelőli az f függvény értelmezési tartományát (Domain), Ra(f) pedig az értékkészletét (Range).
A valóságban elvégzett kísérletsorozatot jellemezzük az A bekövetkezés relatív gyakoriságának várható értékével. Hasonlóan a szimulációbeli kísérletben. Ha P(X(A)=1)=P(R(A)=1), akkor elfogadjuk ekvivalenseknek.
Itt kell folytatni tovább az R(A) valószínűségi változó értelmezését, azaz a Do(R) osztályfelbontását úgy, hogy P(R(A)=1) = P(A) teljesüljön.
Legyen
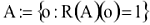
azaz Do(R) A-hoz rendelt osztálya!
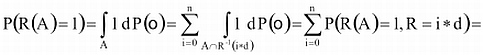
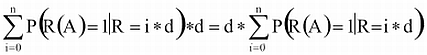
Felhasználtuk, hogy P(R=i*d)=d.
Mivel a véletlenszám-generátorunk d-finomságú, így a véletlenszámot egyértelműen meghatározza az őt tartalmazó [i*d,(i+1)*d) részintervallum. Tehát vagy az adott osztályba kell tartozzon a teljes részintervallum, vagy diszjunkt tőle. Következésképpen P(R(A)=1|R=i*d)=1 vagy 0.
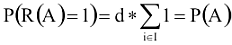
Itt az I azon indexek halmaza, amely részintervallumon a fenti valószínűség 1.
Vagyis olyan Do(R)-et kell kiválasztani, amely részintervallumainak száma:
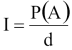
Érdemes észrevenni, hogy P(A)<d esetben (ami előfordulhatna, ha a számítás pontossága nagyobb a véletlenszám-generátorénál) az A eseményhez nem adható meg részintervallum.
Erre a legkézenfekvőbb a [0,P(A)) intervallumot kiválasztani (bár éppúgy megfelelő lenne az [1-P(A),1) választás is), hiszen részintervallumainak száma a fenti. (Megjegyezzük, hogy akár nem érintkező részintervallumok egyesítése által meghatározott halmaz is megfelelne, ha a fenti számú részintervallumból áll. Ez számítástechnikai szempontból azonban nem érdekes, hisz túl sok információt kell a halmazhoz tárolni.)
Összefoglalóan az R(A):[0,1){1,0},
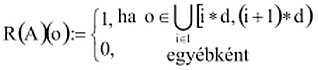
Nos, az R(A) valószínűségi változó már magától értetődően előáll az R segítségével, csak az R(A)=1 és R<P(A) események azonosságát kell észrevennünk. (Bevezetjük a p:=P(A) jelölést.)
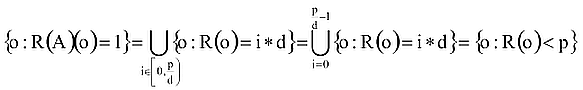
A. A és B diszjunkt események, együtt teljesen lefedik a biztos eseményt
Legyen az A esemény P, a B esemény pedig Q valószínűségű! Ha R<p, akkor az A eseményt bekövetkezettnek tekintjük, egyébként pedig a B-t.
Vegyük a [0,1) intervallumot, osszuk két részre:

Ha egy véletlenszám az első felébe esik, akkor az A esemény következik be, ha nem, akkor pedig a B.
...
Ha véletlenszám<P akkor A esemény különben B esemény
...
Ritkán kell ilyen egyszerű esetet szimulálni, de sokszor ehhez hasonló módon, elvében megegyezően építhető föl a program szimulációs magja. Néhány ilyen esetet tekintünk át.
B. A és B nem diszjunkt események, de együtt teljesen „lefedik” a biztos eseményt
Az AB=0 nem teljesül, ezért nem alkalmazható az 1. módszer. Azonban könnyen megteremthető a kapcsolat 1-gyel, ha az {A,B} helyett az {A’:=A-AB, C:=AB és B’:=B-AB} eseményrendszert tekintjük. Az {A’,C,B’} már teljes eseményrendszert alkot.
Tehát
Mivel A+B=Ω (Ω a biztosan bekövetkező esemény), így P(A)+P(B)-P(AB)=1 egyenlőségnek igaznak kell lennie, következésképpen P(AB)=P(A)+P(B)-1.
Ezen eredményekből már könnyen származtathatók az alábbiak.
A,B: AB≠0, A+B=Ω események szimulálása:
Jelölje P az A, Q pedig a B esemény valószínűségét! A fentiek szerint a [0,1) intervallumot az alábbiak szerint osztjuk három részre:

...
x:=véletlenszám
Ha x<P akkor A esemény
Ha x≥1-Q akkor B esemény
...
C. A és B diszjunktak, de nem adják ki a biztos eseményt
Az A+B=Ω feltétel nem teljesülése miatt megint nem alkalmazható az 1. Kiegészítve az {A,B} rendszert egy fiktív C (=Ω-A-B) eseménnyel: már készen vagyunk.
A,B: AB=0, A+B≠ Ω események szimulációja:
Jelölje P az A, Q pedig a B esemény valószínűségét! A fentiek szerint a [0,1) intervallumot az alábbiak szerint osztjuk három részre:

...
x:=véletlenszám
Ha x<P akkor A esemény
különben ha x<P+Q akkor B esemény
...
D. Az A, B és C eseményekről a következőket tudjuk:
A⊆B+C, és B, C események diszjunktak, és ismert a P(B), P(C) és P(AB). Ekkor elemi úton megkapható a P(A), a P(BA) és a P(B-A), ahol a -A az A komplemensét jelöli:
Ekkor
Az eddigi eseteket egyszerűségük és alapvető voltuk miatt nevezhetjük a szimuláció elemi eseteinek. A most következők már összetettebbek, de mindegyikük magától értetődően adódik az elemiekből.
E. n eseményből álló teljes eseményrendszer, azonos valószínűséggel
N eseményünk van, kizáróak, rajtuk kívül más nem lehet, egyenlő valószínűségűek. Ekkor minden esemény pontosan 1/N valószínűségű.
Ekkor az esemény indexe könnyebben meghatározható. Legyen P:=P(Ak)=1/n ∀k-ra!
Mivel
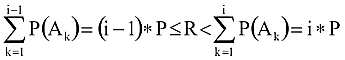
azaz
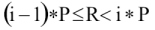
Az egyenlőtlenséget n-nel szorozva kapjuk, hogy
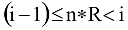
esetén kell bekövetkeznie az Ai eseménynek. Tehát az esemény sorszáma így határozható meg: i:=[n*R+1].
...
V:=egészrész(N*véletlenszám+1)
...
F. n eseményből álló teljes eseményrendszer
A továbbiakban felhasználjuk a tárgyalt alapeset azon fontos eredményét, hogy a szimulálni kívánt eseményhez (ott az A-hoz, illetve a -A-hoz) a [0,1) intervallum megfelelő felosztását kell csak megkeresni.
Az A1,...,An események teljes eseményrendszer volta azt jelenti, hogy
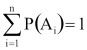
és i≠k esetén
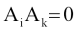
Tehát minden esetben pontosan (!) 1 esemény következik be.
Ebből szemre is látszik, hogy olyan Ii részintervallum-felosztások között lelhető meg a keresett, amelyekre teljesülnek az alábbi feltételek:
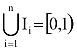
és i≠k esetén
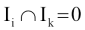
Azzal, hogy a [0,1) felosztását eleve folytonos részintervallum-partíciókra szűkítettük le, adódik, hogy Ii csak [ai,bi) alakú lehet. Az általánosság megszorítása nélkül feltehetjük, hogy az [ai,bi) intervallumok sorrendjét az ai-k sorrendjével rögzítjük. (Ez legfeljebb az intervallumok más sorrendben való felsorolását jelenti!)
Tehát az első feltétel a bi≥ai+1-t kívánja meg, másrészt a második a bi≤ai+1-t vonja maga után, amik csak a bi=ai+1 esetben elégíthetők ki egyszerre.
Ez a részintervallum-partícionálás még csak a fenti két feltételt veszi figyelembe, semmi köze sincs az események valószínűségeihez. Az ai-k megadása úgy kell történjen, hogy az [ai,bi) intervallum hossza P(Ai) legyen – ahogy ezt korábban beláttuk –, azaz bi-ai=P(Ai), s a teljesség miatt nyílván a0=0, valamint bn=1.
Következésképpen
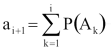
Vegyük észre, hogy tulajdonképpen most is a korábban említett direkt módszert alkalmaztuk, csak épp egy „diszkrét függvény” inverzét kellett képeznünk! Nevezetesen az
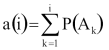
függvényét.
Ahhoz, hogy a szimuláció eredményét helyesnek tarthassuk, az eseményeknek eleget kell tenniük az alábbi két követelménynek:
Az n-elemű teljes eseményrendszer szimulációja történhet így: a szimuláció során az A esemény következett be, ha
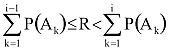
Utaljunk ennek „praktikus” (=program) megvalósítására is! A megfelelő esemény kiválasztásakor nem célszerű az eseményazonosítás minden egyes alkalmával a feltételben szereplő két szummát újra meg újra kiszámolni, hanem járjunk el így:
Véletlenesemény(i):
h:=P(1); i:=1; x:=véletlenszám
Ciklus amíg x≥h[az i. eseményig nem találtuk meg a keresettet]
i:=i+1; h:=h+P(i)
Ciklus vége
Eljárás vége.
Az algoritmusbeli P vektor az Ai események valószínűségeit tartalmazza.
G. Végtelen sok esemény
Végtelen sok eseményünk van, kizáróak, rajtuk kívül más nem lehet, különböző (Pi) valószínűségűek. Ekkor adott tetszőleges ε>0 számhoz legyen m a legnagyobb index, amire Pm>ε!
...
v:=1; h:=P(v); x:=véletlenszám
Ciklus amíg x≥h és v≤m
v:=v+1; h:=h+P(v)
Ciklus vége
...
H. Binomiális eloszlás
Az n független kísérlet során az A esemény bekövetkezésének gyakoriságait {h(A,n)=k} tekintsük elemi eseményeknek! Állítsuk elő ezeket az elemi eseményeket! (A p:=P(A) és n paraméterű binomiális eloszlás generálása.)
Ekkor az A esemény bekövetkezéseinek gyakorisága határozza meg az elemi események halmazát: Ai:={h(A,n)=i}.
A hozzájuk tartozó valószínűségek:
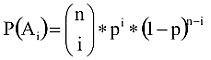
Az Ai teljes eseményrendszer, így az F.-re való hivatkozással elintézettnek is tekinthetjük. Mégis, mielőtt lezárnánk e kérdést vegyük szemügyre az F. alatt szereplő megjegyzéseket!
Az első eset programozásához a következőket érdemes észrevenni:
Binomiális eloszlású véletlenszám előállítható a definíció szó szerinti alkalmazásával is – hányszor következik be egy p valószínűségű esemény n kísérletből:
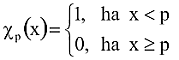
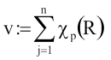
...
v:=0
Ciklus j=1-től n-ig
Ha véletlenszám<p akkor v:=v+1
Ciklus vége
...
I. Geometriai eloszlás
Egy p valószínűségű esemény első bekövetkezésének sorszámára vagyunk kíváncsiak:
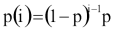
Láthatólag alkalmazható a G. eset, van végtelen sok, egymást kizáró, különböző valószínűségű eseményünk.
Itt is egyszerűbb azonban a definíció szó szerinti alkalmazása:
...
v:=1
Ciklus amíg véletlenszám≥p
v:=v+1
Ciklus vége
...
Belátható,hogy egy véletlenszámra a
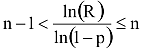
összefüggés éppen p(n) valószínűséggel igaz, azaz
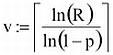
J. n állapotú rendszer szimulációja
Legyen az R rendszer állapotainak halmaza az S véges halmaz. A rendszer adott si∈S állapotból valamely sk∈S állapotba pik valószínűséggel halad. Írjuk meg a rendszer állapotát szimuláló program magját!
Kézenfekvőnek látszik ezt is visszavezetni az A. esetre. Ez könnyen megvalósítható, ha az ott szereplő vektor helyett most mátrixot alkalmazunk az alábbi értelmezéssel: P:=[pik], pik:=P(k. állapot|i. állapot). A mátrix i. sora így egy adott állapotból való átmenetekhez rendeli a valószínűségeket.
Az n állapotú rendszer szimulációja történhet így, ha
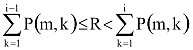
akkor a szimuláció során a rendszer az i. állapotba került (feltéve, hogy ezt megelőzően az m.-ben volt).
Egy kis „elméleti” jellegű kitérő, gyakorlati következményekkel:
Gyakran előfordul, hogy a modellezettről még sztochasztikusan sem áll rendelkezésünkre elegendő információ. Néha ilyenkor is kínál megoldást a szimulációs megközelítés. Ha bizonyos feltételek teljesülése garantálható, akkor két ismert típusú eloszlásra vezethető vissza a probléma.
K. Poisson-folyamatként írható le a jelenség, ha
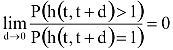
A feltételeket teljesítő jelenségek Poisson-eloszlással írhatók le (k=0,1,...,):
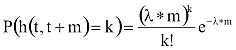
ahol λ a jelenségre jellemző pozitív valós szám.
A Poisson-eloszlás nagy jelentőségű voltát bizonyítja az is, hogy bizonyos feltételek mellett a binomiális eloszlás határértékeként is megkapható! Ez a tény annál is fontosabb, mivel – különösen nagy n-ek-re – a binomiális eloszlású valószínűségi változó szimulálása gyakorlati akadályokba (végrehajtási idő-, vagy helyproblémába) ütközik. Ilyenkor komoly gyakorlati haszonnal jár a Poisson-eloszlásra való át-térés lehetősége.
Állítás: rögzített k-ra, ha n→+∞ és n*p→λ>0, akkor
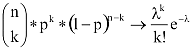
Hogyan lehet Poisson-eloszlású valószínűségi változót szimulálni?
Ahogy korábban láttuk, a megoldáshoz úgy is eljuthatunk – kiindulva az E[0,1) eloszlású véletlenszám-generátorból –, hogy képezzük a Poisson-eloszlás „inverz-függvényét”. A teljes eseményrendszernél alkalmazott ötletből kiindulva azt az n egész értéket kell megtalálnunk, amelyre igaz
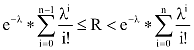
A Poisson-eloszlású véletlenszámokat generáló függvény megírásánál az alábbi rekurzív képletből lehet kiindulni:
T(n):=T(n-1)*λ/n; S(n):=S(n-1)+T(n)
…
T(0):=1; S(0):=T(0); v:=1
x:=véletlenszám*exp(λ)
Ciklus amíg x≥S(v-1)
T(v):=T(v-1)*λ/v
S(v):=S(v-1)+T(v)
v:=v+1
Ciklus vége
…
L. Gauss-folyamathoz való konvergencia
Független valószínűségi változók összege normális (Gauss-) eloszlást követ, ha a tagok száma minden határon túl növekszik. A pontosabb határeloszlás-tétel a következő:
Ha X1,… Xn valószínűségi változók függetlenek és egyforma eloszlásúak, létező m várható értékkel és s szórással, akkor az
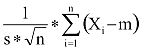
összeg aszimptotikusan standard normális eloszlású, vagyis
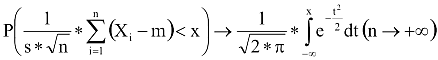
A véletlenszám-generátorunk esetén – mint láttuk – m=1/2 és s=1/gyök(12). Most már minden ismeret birtokunkban van ahhoz, hogy megadjuk azt az algoritmust, amellyel közelítőleg N(μ,σ) eloszlású véletlenszámot generálhatunk.
Egy G N(μ,σ) normális eloszlású véletlenszám előállítása:
...
S:=0 [n a közelítésben résztvevő [0,1)- véletlenszámok száma]
Ciklus i=1-től n-ig
S:=S+véletlenszám
Ciklus vége
...
Most rendelkezünk egy közelítőleg
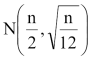
eloszlású véletlenszámmal, már csak a kérdéses normális eloszlásúvá transzformálása maradt hátra:
G:=(σ*gyök(12))/gyök(n)*(S-n/2)+μ
Ha n=12*m2, akkor:
G:=σ/m*(S-n/2)+μ
Igazolható, hogy viszonylag kicsi n esetére (n<10) is elég jó a közelítés. A pontosság az összeadandók számának növelésével tovább javítható, persze a műveletigény rovására. Speciális módszerekkel az n növelése nélkül is elérhető javulás.
Ahogy a Poisson-eloszlásnál örülni lehetett annak, hogy helyettesíteni – pontosabban: közelíteni – tudtuk vele a binomiális eloszlást, úgy ez az öröm még teljesebb lehet a normális eloszlású véletlenszám szimulálására adott fenti egyszerű algoritmus és az alábbi tétel ismeretében.
Moivre-Laplace tétel:
Rögzített z0 és z1 valós számok esetén, ha n→+∞, akkor
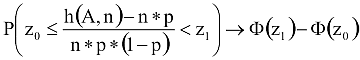
E tétel gyakorlati haszna akkor nyilvánvaló, ha a binomiális eloszlás realizálása számolásigényessége miatt nem kivitelezhető, az egyszerűen megvalósítható normális eloszlásúval való közelítéssel szemben.
 |
 |
 |
| Készült az "Országos koordinációval a pedagógusképzés megújításáért” című TÁMOP-4.1.2.B.2-13/1-2013-0007 pályázat keretében. (ISBN 978-963-284-631-6) | ||
A tananyag az ELTESCORM keretrendszerrel készült