Import List


module Sets.Recursive where

open import Sets.Enumerated using (Bool; true; false)

The effect of this open import declaration is the same as if we copied the definition of Bool type here. Note that we enumerated the constructors of Bool too.

More about import declarations come later.

Peano representation

We are looking for a representation natural numbers. The simplest choice is the Peano representation which corresponds to the unary numeral system:

term interpretation in decimal form
zero 0
suc zero 1
suc (suc zero) 2
suc (suc (suc zero)) 3
... ...

Definition of ℕ

In Agda the definition


data ℕ : Set where
  zero :     ℕ
  suc  : ℕ → ℕ

yields the infinite set of judgements

ℕ : Set
zero : ℕ
suc zero : ℕ
suc (suc zero) : ℕ
suc (suc (suc zero)) : ℕ
...

Type-checking of expressions

With the Emacs command C-c C-d one can get Agda to type-check a given expression (d stands for 'deduce').

Example: Hit C-c C-d and enter suc (suc zero).

Exercise: Try to type-check the following expressions:

Binary representation of ℕ


data ℕ⁺ : Set where
  one      :      ℕ⁺
  double   : ℕ⁺ → ℕ⁺
  double+1 : ℕ⁺ → ℕ⁺

yields (without ordering)

ℕ⁺ : Set
one : ℕ⁺
double one : ℕ⁺
double+1 one : ℕ⁺
double (double one) : ℕ⁺
double+1 (double one) : ℕ⁺
double (double+1 one) : ℕ⁺
double+1 (double+1 one) : ℕ⁺
double (double (double one)) : ℕ⁺
...

And


data ℕ₂ : Set where
  zero :      ℕ₂
  id   : ℕ⁺ → ℕ₂

yields

ℕ₂ : Set
zero : ℕ₂
id one : ℕ₂
id (double one) : ℕ₂
id (double+1 one) : ℕ₂
id (double (double one)) : ℕ₂
id (double+1 (double one)) : ℕ₂
...

Soon we will prove in Agda that ℕ and ℕ₂ are isomorphic with the following relation:

ℕ ℕ₂
zero zero
suc zero id one
suc (suc zero) id (double one)
suc (suc (suc zero)) id (double+1 one)
... ...

Exercise: How 9 is represented in ℕ₂? Type-check the expression!

Question: why didn't we use one data definition with 4 constructors zero, one, double, double+1?

Rationale behind different representations

Each representation has its merit.

Exercise: Guess which representation (ℕ or ℕ₂) is better for the following tasks!

A good strategy is to choose the right representation for each task and convert values between different representations.

Exercise

(Several solutions are possible.)

Binary trees


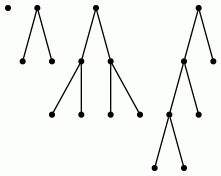
data BinTree : Set where
  leaf : BinTree
  node : BinTree → BinTree → BinTree

yields

BinTree : Set
leaf : BinTree
node leaf leaf : BinTree
node (node leaf leaf) leaf : BinTree
node leaf (node leaf leaf) : BinTree
node (node leaf leaf) (node leaf leaf) : BinTree
...

BinTree elements are good for representing binary trees (just the shapes without data).

Exercise: define binary trees according to the following shapes!

Binary tree shapes

Binary tree shapes

Exercises