Direkt címzés (Direct addressing)

A hasító táblák legegyszerűbb megvalósítása a direkt címzés. Ezt akkor használhatjuk, ha a kulcshalmaz nem túl nagy. Egy $m$ méretű $T$ tömbben (hasítótáblában) tároljuk a rekordokra mutató pointereket úgy, hogy a tömb $k$ indexű tagja, a $k$ kulcsú rekordra mutat. Ha nincs $k$ kulcsú rekord, akkor $T[k]$ nullpointer.

$T:D^*[m]$, ahol a $T$ egy $m$ méretű tömb (hasítótábla), amely $D$ típusú pointereket tárol.

$D$

$+ \space k : U$
$+ \space ...$

Gyakran még az sem szükséges, hogy az objektum kulcsmezőjét tároljuk, hiszen ha megvan egy elem tömbbeli indexe, akkor megvan a kulcsa is, ugyanis egy $k$ kulcsú elem a $k$-adik résben tárolódik.

$init(T : D^*[m])$

	$i := 0 \space to \space m-1$
	$T[i] := \emptyset$

$find(T : D^*[]; k:U) : D^*$

$\text{return} \space T[k]$

$insert(T : D^*[]; p:D^*) : \mathbb{B}$

$T[p \rightarrow k] = \emptyset$
$T[p \rightarrow k] := p$		$\text{return} \space false$
$\text{return} \space true$

$remove(T : D^*[]; k:U) : D^*$

$p:=T[k]$
$T[k] := \emptyset$
$\text{return} \space p$

Direkt címzés hátrányai:

Ha a kulcshalmaz nagy, akkor egy nagy méretű $T$ tömböt kell tárolni, ami a gépek memóriájának korlátozott mérete miatt nem célszerű vagy egyenesen lehetetlen. Továbbá lehetséges, hogy a $T$ által elfoglalt hely legnagyobb része kihasználatlan. Ezért a direkt címzés nem alkalmazható nagy méretű kulcshalmaz esetén.

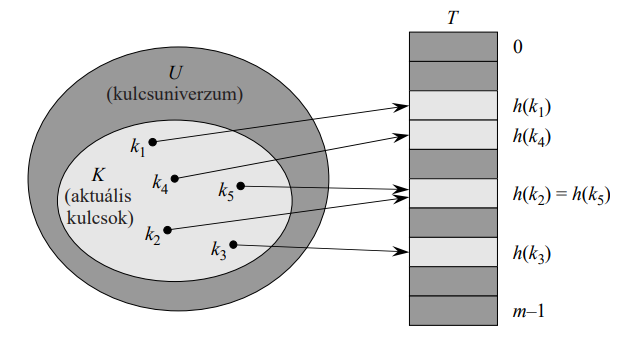
Megtörténhet, hogy két kulcs is ugyanarra a résre képződik le. Ezt a helyzetet ütközésnek nevezzük. Az ütközések nyomán keletkező konfliktusokat fel kell oldani, viszont ezt a direkt címzés nem tudja kezelni. A kulcsütközés feloldása jellemzően két módon történik: láncolt hasheléssel vagy nyílt címzéses hasheléssel.

Műveletigény:

$T_{init}(m) \in \Theta(m)$
A másik három művelet futási ideje $\Theta (1)$