Ha a direkt címzés nem alkalmazható, vagy nem gazdaságos, hasító függvényt
alkalmazunk. Ez esetben az elem a $h(k)$ helyre kerül, vagyis egy $h$ hasító függvényt használunk
arra,
hogy a rést a $k$ kulcsból meghatározzuk.
A láncolásnál az ugyanarra a résre leképződő elemeket összefogjuk egy láncolt
listába. $m$ darab S1L listában tároljuk az adatrekordokat. Az $i$-edik rés egy pointert
tartalmaz,
mely az $i$ címre leképződő elemek listájának fejére mutat. Ha nincs ilyen elem, akkor a $i$-edik
rés
nullpointert tartalmaz.
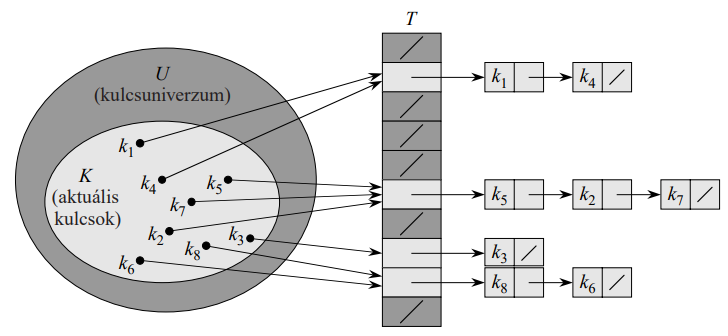
Beszúráskor a megfelelő lista elejére szúrjuk be az új elemet azért, hogy a
beszúrás
minél egyszerűbb legyen. A beszúrás előtt ellenőrizzük a megfelelő listát, a duplikált kulcsok
elkerülése céljából.
$T:E1^*[m]$, ahol a $T$ egy $m$ méretű tömb (hasítótábla), amely $E1$ típusú
pointereket tárol.
| $E1^*$ |
$+ \space key : U$
$+ \space next : E1^*$
$+ \space ...$ |
| $+ \space E1() \{ next := \emptyset \}$ |
|
$i := 0 \space to \space m-1$ |
| $T[i] := \emptyset$ |
| $k := p \rightarrow key$ |
| $s := h(k)$ |
$searchS1L(T[s], k) = \emptyset$
|
| $p
\rightarrow next := T[s]$ |
$\text{return} \space false$ |
| $T[s] := p$
|
| $\text{return} \space true$ |
| $\text{return} \space searchS1L(T[h(k)], k)$
|
|
$q \neq \emptyset \land q \rightarrow key \neq
k$ |
| $q := q \rightarrow next$ |
| $\text{return} \space q$ |
| $s := h(k)$ |
| $p := \emptyset$ |
| $q := T[s]$ |
|
$q \neq \emptyset \land q \rightarrow key \neq
k$ |
| $p := q$ |
| $q := q \rightarrow next$ |
$q \neq \emptyset$
|
$p = \emptyset$
|
$\text{SKIP}$ |
| $T[s] := q
\rightarrow next$ |
$p
\rightarrow next := q \rightarrow next$ |
| $q \rightarrow next := \emptyset$ |
| $\text{return} \space q$ |
Műveletigény:
- $T_{init}(m) \in \Theta(m)$
- A másik három művelet futási ideje $mT(n) \in \Theta (1)$, $MT(n) \in \Theta (n)$, $AT(n, m) \in
\Theta (1 + \alpha)$
