A naiv módszer fix hosszú kódot használt. Ezzel általában nem érhetjük el a megfelelő tömörítést. Viszont betűnkénti kódolás esetén a változó hosszúságú kód alkalmazása tekintélyes megtakarítást eredményez, ha gyakori karaktereknek rövid, ritkán előforduló karaktereknek hosszabb kódszavakat feleltetünk meg. A Huffman-kódolás egy betűnkénti optimális kódolás, azaz az ilyen kódolások között a lehető legrövidebb prefixmentes kód érhető el vele adott adat esetén.

A Huffman-kód változó hosszúságú kódot ad, mégis egyértelműen dekódolható. Ez azért lehetséges, mert prefixmentes kód (vagy prefix-kód). Ez azt jelenti, hogy egyetlen karakter kódja sem prefixe semelyik másik karakter kódjának sem. Másképp a kódszavakra igaz, hogy egyik sem kezdőszelete egy másiknak. Pl.: $\{101, 011, 1010\}$ nem prefixmentes kód, mert az $101$ az $1010$ kezdőszelete, azaz prefixe.

Kódolás működése:

Olvassuk végig a szöveget és határozzuk meg az egyes karakterekhez tartozó gyakoriságokat. Hozzunk létre minden karakterhez egy csúcsot és helyezzük el egy minimum prioritásos sorban a gyakoriságok szerint. Vegyünk ki két csúcsot a prioritásos sorból és hozzunk létre számukra egy szülő csúcsot. A szülő-gyerek éleket címkézzük, nullával és eggyel. Általában a bal oldali lesz a $0$ és a jobb oldali az $1$, de ez tetszőleges. Eljárhatunk úgy is, hogy a kisebb gyakoriságú gyerekhez vezető él legyen a $0$ és a nagyobbikhoz vezető él az $1$. Helyezzük el a szülő csúcsot a prioritásos sorba gyerekei gyakoriságának összegét használva kulcsként. Ismételjük meg az előzőeket, ha több mint egy csúcs szerepel a sorban. Olvassuk ki a karakterekhez tartozó kódszavakat a kódfából. Olvassuk végig újra a bemenetet és kódoljuk azt karakterenként.

Példa:

Tömörítsük az $ABRAKADABRA$ szöveget. Először számoljuk meg a karakterek gyakoriságát és ezt helyezzük el egy minimum prioritásos sorban.

$<(D /1), (K/1), (B/2), (R/2), (A/5)>$

Majd vegyük ki a kettő legkisebbet és vonjuk össze őket addig, amíg egy csúcs nem marad.

$<(DK /2), (B/2), (R/2), (A/5)>$

$<(R /2), (DKB/4), (A/5)>$

$<(A /5), (DKBR/6)>$

$<(DKBRA /11)>$

Ezek alapján felépíthetjük a fát. Balra nullát írunk jobbra egyet.

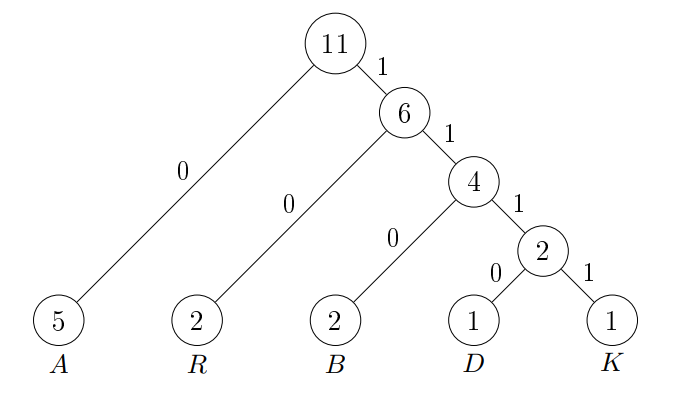
A kódfából megkaphatjuk a karakterek kódjait, ha a fa gyökerétől kezdve haladunk lefelé a levelekig.

Karakter	Kód
$A$	$0$
$B$	$110$
$D$	$1110$
$K$	$1111$
$R$	$10$

Az $ABRAKADABRA$ szöveg Huffman-kódja: $01101001111011100110100$.

Huffmann-kódolás tulajdonságai:

A Huffman-kódolás folyamata általában nem-determinisztikus, azaz több megoldása is lehet. Egyrészt, ha több azonos gyakoriság van, akkor bármelyiket választva Huffman-kódolást kapunk. Másrészt a $0$ és $1$ szerepe felcserélhető a kódfában.

• A tömörítendő fájlt, illetve szöveget kétszer olvassa végig.
• A kódfa szigorúan bináris fa.
• A tömörített fájl a kódfát vagy a kódtáblát is tartalmazza.
• A tömörített kód hossza nem függ a nem-determinisztikus viselkedés feloldásától.
• A Huffman-kódolás optimális a betűnkénti, prefixmentes kódolások között, azaz nem létezik olyan betűnkénti, prefixmentes kódolás, ami rövidebb kódot eredményezne, mint a Huffman-kódolás.

Kódoláshoz szükséges bitek száma:

A kódoláshoz szükséges bitek száma a következő képlettel számolható ki. Legyen $c$ egy karakter a $\Sigma$ abc-ben.

$\sum_{c \in \Sigma}$ $c$ előfordulása $\cdot$ $c$ kódjának hossza

Dekódolás működése:

A dekódoláshoz ismernünk kell a kódolt adatot és a kódfát. Ezek ismeretében a dekódolás is meglehetősen egyszerű prefixmentes kód esetén, mivel nincs olyan kódszó, amely kezdőszelete lenne egy másiknak, így egyértelmű, hogy a kódolt állomány melyik kódszóval kezdődik.

A kitömörítést is karakterenként végezzük. Mindegyik karakter kinyeréséhez a kódfa gyökerétől indulunk, majd a tömörített kód sorban olvasott bitjeinek hatására $0$ esetén balra, $1$ esetén jobbra lépünk lefelé a fában (de ez nem-determinisztikus), mígnem levélcsúcshoz érünk. Ekkor kiírjuk a levelet címkéző karaktert, majd a Huffman-kódban a következő bittől, a kódfában újra a gyökerétől folytatjuk a kitömörítést, amíg a tömörített kódon végig nem érünk.

Gyakorlati alkalmazása:

A Huffman-kódolást felhasználják szövegek küldésénél, illetve hagyományos tömörítési formátumoknál, mint például a GZIP.