Quicksearch

Ez az algoritmus a Boyer-Moore mintaillesztés több változata körül az, amelyiknek a Quick Search nevet adta a szerzője (Horspool).

Ennél az algoritmusnál általában egynél nagyobb lépésekben növeljük a $P[0..m)$ minta eltolását a $T[0..n)$ szöveghez képest úgy, hogy biztosan ne ugorjunk át egyetlen érvényes eltolást sem. A tényleges mintaillesztés előtt egy előkészítő fázist hajt végre, ami nem függ a szövegtől, csak a mintától.

Az alapötlet az, hogy ha elromlik az illeszkedés, akkor nézzük a szövegben a minta utáni karaktert, és úgy toljuk el a mintát, hogy illeszkedjen a szöveg ezen karakteréhez. Ha a mintában nem szerepel ez a karakter, akkor átugorjuk a mintával. Az új vizsgálatot mindig a minta elejéről nézzük . A mintával való ugrás végrehajtásához bevezetjük a $shift$ függvényt.

Működési elve:

A $shift$ függvény az ABC minden betűjére megadja az ugrás nagyságát, amelyet akkor tehetünk, ha az illeszkedés elromlása esetén az illető betű lenne a szöveg minta utáni első karaktere.

Ha a szöveg minta utáni első karaktere nem fordul elő a mintában, akkor bármely olyan illesztés sikertelen lenne, ahol a szöveg fedésben lenne a mintával. Tehát ezt a pozíciót átugorhatjuk a mintával, és a minta elejétől kezdhetjük újra az illeszkedés vizsgálatát.

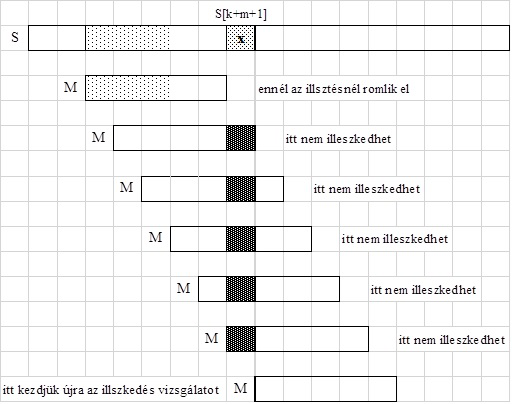
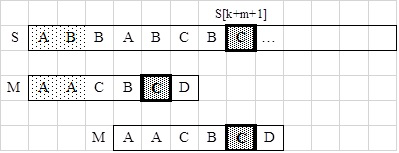
Ha a szöveg minta utáni első karaktere előfordul a mintában, akkor vegyük a mintabeli előfordulások közül jobbról az elsőt és annyi pozícióval léptessük jobbra a mintát, hogy ez a mintabeli karakter fedésbe kerüljön a szöveg karakterével. Majd a minta elejétől kezdve vizsgáljuk meg újra az illeszkedést.

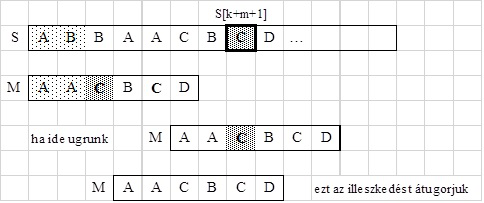
Azért kell jobbról az első mintabeli előfordulását tekinteni, mert ha létezik egy ettől balra lévő előfordulás is, és amennyiben azt választanánk, akkor esetleg átlépnénk egy jó illeszkedést.

Működése:

Az algoritmus a $shift$ függvény értékeinek kiszámításával kezdődik, amihez felhasználja a mintát. Majd megpróbáljuk illeszteni a mintát. Amennyiben az illeszkedés elromlik, akkor a $shift$ függvénynek megfelelően változtatjuk az eltolás mértékét és ismételten megpróbáljuk illeszteni a mintát. Ez a folyamat addig tart, amíg végig nem értünk a szövegen a mintával.

Műveletigény:

$MT(n,m) \in \Theta((n-m+2) \cdot m)$, ha $T = AA . . . A$ és $P=A...A$.
$mT(n,m) \in \Theta(\frac{n}{m+1} + m)$, ha a szöveg és a minta diszjunktak.

Gyakorlati alkalmazása:

Mintaillesztő algoritmusokat használnak a plágium keresők, böngésző keresőmotorjai. Használják továbbá spamek kiszűréséhez, szöveg szerkesztő programokban a helyesírásunk ellenőrzéséhez, illetve a bioinformatikában DNS láncokban egy-egy szakasz megtalálásához is.

Animáció

Struktogram

$QuickSearch(T: \sum [n]; P: \sum [m]; S : \mathbb{N} \{\})$

$initShift(P)$
$S := \{\}$
$s := 0$
	$s + m \leq n$
	$match(T, P, s)$
	$S:=S \cup \{s\}$	$\text{SKIP}$
	$s+m < n$
	$s += shift(T[s+m])$	$\text{break}$

$initShift(P: \sum [m])$

	$\forall \sigma \in \sum$
	$shift(\sigma) := m + 1$
	$j := 0 \space to \space m - 1$
	$shift(P[j]) := m-j$

Animáció

Struktogram

$QuickSearch(T: \sum [n]; P: \sum [m]; S : \mathbb{N} \{\})$

$initShift(P)$
$S := \{\}$
$s := 0$
	$s + m \leq n$
	$match(T, P, s)$
	$S:=S \cup \{s\}$	$\text{SKIP}$
	$s+m < n$
	$s += shift(T[s+m])$	$\text{break}$

$initShift(P: \sum [m])$

	$\forall \sigma \in \sum$
	$shift(\sigma) := m + 1$
	$j := 0 \space to \space m - 1$
	$shift(P[j]) := m-j$

Feladatok

Az alábbi feladatok a gyakorlatokon elvégzendő kötelező, illetve gyakorló feladatok.