Kétváltozós függvények ábrázolása
1 Bevezetés
Feladat egy kétváltozós valós függvény kirajzolása különféle megjelenítési módszerekkel. Például:
· szintvonalakkal,
· pontfelhővel,
· téglalapokkal,
· folytonos szakaszokkal,
· …
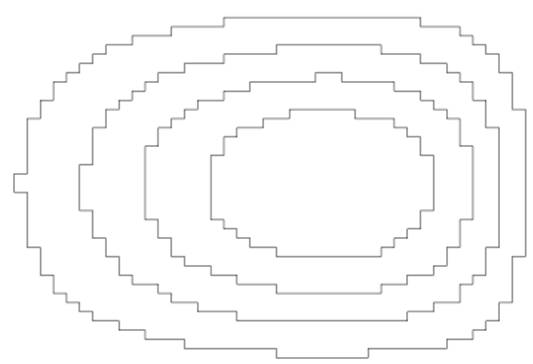
Az elvárásokat legjobban az alábbi, futás során keletkezett ábrasor fejezi ki,
|
|
|
1.
ábra. Egy futási kép – szintvonalas ábrázolás (2-irányú vonalakkal) |
|
|
|
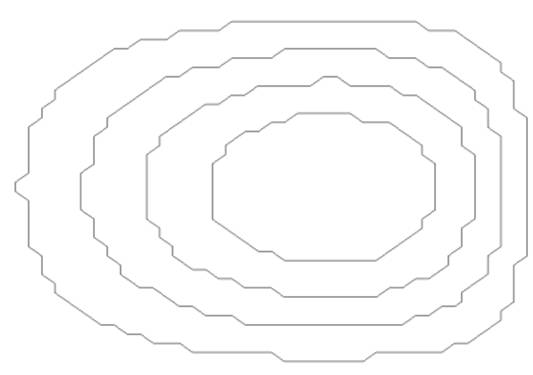
2.
ábra. Egy futási kép – szintvonalas ábrázolás (4-irányú vonalakkal) |
|
|
|
3.
ábra. Egy futási kép – pontfelhővel |
|
|
|
4.
ábra. Egy futási kép – téglalapokkal |
valamint egy próba: Fv2Mo.exe.
2 Útban a megoldás felé
2.1 Jelölések
Alapadatok:
· f – függvénykapcsolat; f: Df ® Rf,
· Df – értelmezési tartomány = [1..MaxN]´[1..MaxN]ÌN´N
· Rf – értékkészlet = [0..yMax] ÌR
3 Módszerek – algoritmusok
Algoritmikus adatok és egyéb kellékek:
Függvény f(Konstans
i,j:Egész):Valós
…
Konstans MaxN
: Egész(50)
SzvDb: Egész(5)
Típus TFvTábla = Tömb(1..MaxN,1..MaxN:Valós)
TSzintVonalak = Tömb(1..SzvDb:Valós)
Konstans szv :
TSzintVonalak(0.2,0.4,0.6,0.8,1.0)
Változó fvt:TFvTábla [egy
fv. gráfjának pontjai]
sDb,oDb:Egész [rajzolandó sorok, oszlopok száma]
sk,ok:Egész [rácsháló sor-, oszlopköz mérete]
yMax,ny:Valós [fv. maximuma, nyújtási tényező]
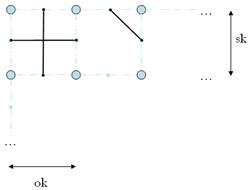
3.1
Rajzolás merőleges szintvonalakkal
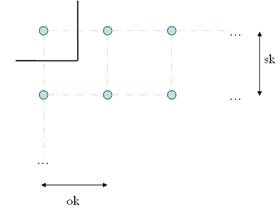
A lényeg: minden (?!?) pont és jobb oldali szomszédja közé meghúzzuk a felező merőlegest, ha közöttük megy (legalább egy) szintvonal. Ugyanígy teszünk a pont és alatta levő szomszédjával is. (Így nem járhatunk el a jobb szélső oszlop és a legalsó sor pontjaival. Ezeket „egyedileg” kezeljük.)
|
|
|
5.
ábra. Megengedett 2 szintvonal. |
Eljárás SzintVonalasRajzolás1:
Változó
i,j:Egész
sk:=MaxY Div sDb; ok:=MaxX Div oDb;
Ciklus i=1-től sDb-1-ig
Ciklus
j=1-től oDb-1-ig
Ha
szintvonal(fvt(i,j),fvt(i,j+1)) akkor
Függőleges(i,j)
Ha
szintvonal(fvt(i,j),fvt(i+1,j)) akkor
Vízszintes(i,j)
Ciklus vége
Ciklus vége
Ciklus
j=1-től oDb-1-ig
Ha
szintvonal(fvt(sDb,j),fvt(sDb,j+1)) akkor
Függőleges(sDb,j)
Ciklus vége
Ciklus
i=1-től sDb-1-ig
Ha
szintvonal(fvt(i,oDb),fvt(i+1,oDb)) akkor
Vízszintes(i,oDb)
Ciklus vége
Eljárás vége.
Függvény Szintvonal(Konstans y1,y2:Valós):Logikai
Változó
k:Egész
x:Valós
x:=szv(1)*yMax; k:=1
Ciklus
amíg (x<y1) és (x<y2) [eldöntés tétel kiválasztás szerűen]
k:+1; x:=szv(k)*yMax
Ciklus
vége
Szintvonal:=(x<y1) vagy (x<y2)
Függvény vége.
Eljárás Függőleges(Konstans i,j:Egész):
Szakasz(j*ok,MaxY-i*sk,j*ok,MaxY-i*sk+sk)[1]
Eljárás vége.
Eljárás Vízszintes(Konstans i,j:Egész):
Szakasz(j*ok,MaxY-i*sk,j*ok-ok,MaxY-i*sk)
Eljárás vége.
3.2
Rajzolás 4-irányú szintvonalakkal
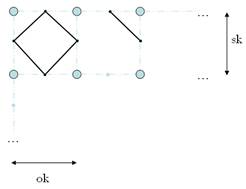
A túl szögletes vonalakon úgy segítünk, hogy 45 fokos egyeneseket is megengedünk. Ekkor az adott pont és 3 szomszédját vesszük figyelembe. Világos, hogy a négy szomszédos pont közötti szakaszfelező pontok száma: 0, 2 vagy 4 lehet. A 4 esete sajnálatos módon kétféle szintvonal összekötést is jelenthet: egy keresztre, ill. egy rombuszra emlékeztető. Ráadásul a négy adat alapján nem is eldönthető, hogy melyik.
|
|
|
|
6.
ábra. Megengedett szintvonalak – 2 változat. |
|
Típus
TSzintPontok=Tömb(1..4:Rekord(sor,oszlop:Egész))
Eljárás SzintVonalasRajzolás2:
Változó
x:Valós;
db,i,j,k:Egész;
szint:TSzintPontok
sk:=MaxY Div sDb; ok:=MaxX Div oDb
Cilus
i=1-től sDb-1-ig
Cilus j=1-től oDb-1-ig
db:=0 [kiválogatás, cikluskibontással!]
Ha szintvonal(fvt(i,j),fvt(i,j+1)) akkor
db:+1
szint(db).sor:=i*2; szint(db).oszlop:=j*2+1
Elágazás vége
Ha szintvonal(fvt(i,j),fvt(i+1,j)) akkor
db:+1
szint(db).sor:=i*2+1; szint(db).oszlop:=j*2
Elágazás vége
Ha szintvonal(fvt(i+1,j),fvt(i+1,j+1)) akkor
db:+1
szint(db).sor:=i*2+2; szint(db).oszlop:=j*2+1
Elágazás vége
Ha szintvonal(fvt(i,j+1),fvt(i+1,j+1)) akkor
db:+1
szint(db).sor:=i*2+1; szint(db).oszlop:=j*2+2
Elágazás vége
Elágazás
db=2 esetén Egyenes(szint)
db=4 esetén Kereszt(szint) [2]
Elágazás vége
Ciklus vége
Ciklus vége
Eljárás vége.
Eljárás Egyenes(Konstans
szint:TSzintPontok):
Szakasz(szint(1).oszlop*ok Div 2, MaxY-szint(1)*sk Div 2,
szint(2).oszlop*ok Div 2, MaxY-szint(2).sor*sk Div 2)
Eljárás vége.
Eljárás Kereszt(Konstans
szint:TSzintPontok):
Változó
s1,o1,s2,o2:Egész
s1:=MaxY-szint(1).sor*sk Div 2; o1:=szint(1).oszlop*ok Div 2
s2:=MaxY-szint(2).sor*sk Div 2; o2:=szint(2).oszlop*ok Div 2
s3:=MaxY-szint(3).sor*sk Div 2; o3:=szint(3).oszlop*ok Div 2
s4:=MaxY-szint(4).sor*sk Div 2; o4:=szint(4).oszlop*ok Div 2
Szakasz(o1,s1,o3,s3); Szakasz(o2,s2,o4,s4)
Eljárás vége.
3.3
Pontfelhős rajzolás
A lényeg: minden y-értékhez a nagyságával arányos sűrűségű „felhődarabot” generálunk. A felhődarab sk*ok pixelméretű. E pixelek közül kell megfelelő számút kigyújtani.
Kétféle elképzelés lehet erre.
1) fvt(i,j)/(Max(ii,jj) fvt(ii,jj))*sk*ok darab kigyújtott pont legyen; vagy
2) az sk*ok pixel mindegyike fvt(i,j)/(Max(ii,jj) fvt(ii,jj)) valószínűséggel legyen kigyújtva.
Az első pontos tud lenni, ha ügyelünk a pontkiválasztás egyértelműségére, de a telítéshez közel túl sok ismétlődést kíván. A második csak „várhatólag” ad jó eredményt, de konstans idejű.
Az alábbi algoritmus az első egy variációja, amely nem ügyel a pontkiválasztás egyediségére, de azzal minimalizálja problémát, hogy 50%-ban maximálja a kitöltést. (Az 50% tartozik a maximális függvényértékhez.)
Eljárás PontFelhősRajzolás:
Változó
db,i,j,ii,jj,k:Egész
sk:=MaxY Div sDb; ok:=MaxX
Div oDb
Ciklus i=1-től sDb-ig
Ciklus j=1-től oDb-ig
db:=Kerekít(sqr(fvt(i,j)/yMax)*sk*ok) Div 2
Ciklus
k=1-től db-ig
ii:=Random(sk); jj:=Random(ok)
Pont(j*ok+jj,MaxY-i*sk+ii,1)
Ciklus
vége
Ciklus vége
Ciklus vége
Eljárás vége.
3.4
Téglalapos rajzolás
Lényege: a felület minden pontjának megfeleltetünk egy színezett oszlopot, amelynek magassága a pont „magassága” lesz. A térbeliséget a téglalapok axonometrikus elhelyezésével érjük el. Vagyis az (i,j) indexű fvt(i,j) magasságú ponthoz egy (o,s0) „talppontú”, fvt(i,j) magasságú oszlopot rendelünk. Ahol
o
o:=i*sk+j*ok
o
s:=Kerekít(MaxY-i*sk-fvt(i,j)*ny)
o s0:=Kerekít(MaxY-i*sk)
Mivel az axonometrikus ábrázolás esetén az egyes oszlopok takarhatják egymást, a kirajzolást hátulról kezdve végezzük. Annak érdekében, hogy az egyes oszlopok ne olvadjanak össze, árnyékkal operálunk: ax,ay jelentse az „árnyék kilógását” az oszlop alól balra, ill. felfelé. Hogy a megjelenítést ki lehessen próbálni a különféle árnyékkal, az eljárást velük paraméterezzük. Az oszlopok magasságának maximumát jelöljük MaxMag-gal, amit ismertnek veszünk.
Eljárás TéglásRajzolás(ax,ay:
Egész):
Változó
i,j,o,s,s0:Egész
sk:=(MaxY-MaxMag) Div sDb; ok:=MaxX Div
(sDb+oDb+1)
Ciklus
i=sDb-től 1-ig visszafelé
Ciklus
j=oDb-tól 1-ig visszafelé
o:=i*sk+j*ok; s:=Kerekít(MaxY-i*sk-fvt[i,j]*ny)
s0:=Kerekít(MaxY-i*sk)
OszlopSzin(Fekete)[3];
Oszlop(o+ax-ok,s-ay,o+ax,s0-ay)
OszlopSzin(Kék); Oszlop(o-ok,s,o,s0)
Ciklus vége
Ciklus vége
Eljárás vége.
4 A keretprogram
Lásd Fv2Ker.htm, Fv2Ker.pas.