amelyben Lóti Futi & Co. osztódik,
sőt még telefont is kap.
(Függöny föl!)
Katonai célú feladatok gyakran vezetnek hatalmas adatmennyiségen (mátrixokon) elvégzendő bonyolult számításokra. Persze nem kell okvetlenül hadi példát keresni, ahhoz hogy ilyen feladatot magunk is el tudjunk képzelni. Gondoljunk egy civil, meteorológiai pl. légköráramlási feladatra, amelyhez egy parciális differenciál egyenletrendszert kell megoldani (nagyméretű mátrixokon történő operációt jelent)!
Már az előző felvonásban is felvetődött annak lehetősége, hogy több Lóti Futi jusson szerephez. Nézzük meg ennek vonzatait! A parallel végrehajtás erejét és nehézségeit ízlelgessük egy mindenki által követhető példán, egy aritmetikai kifejezés párhuzamosítása ürügyén:
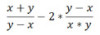
Első lépésünk az, hogy – ismerve a kiértékelés sorrendjét – megrajzoljuk a végrehajtási fáját, melyről – reményünk szerint – sokkal egyértelműbben leolvashatók a dolgok:
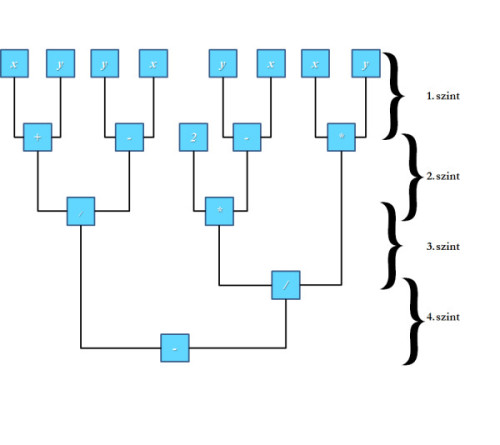 Végrehajtási fa
Végrehajtási faA gráf alapján ránézésre megmondható, mik azok, amik párhuzamosan elvégezhetők:
Így összesen 4 lépésben, maximum 4 processzort használva oldottuk meg az eredetileg 8 lépésben megoldható kiértékelést.
Térjünk vissza az alap, lóti-futis problémára! Hogyan kell „koreografálni” a tisztelt társulatot, melynek több „dudása is lehet ugyanabban a csárdában”. Kézenfekvőnek tűnik, hogy egy mátrixra vezető feladat megoldása esetén kihasználjuk azt számítási sajátosságot, hogy sok azonos számítással juthatunk el a végeredményhez. Ezért nagyszámú, azonos számítási képességű lótis társulást bízzunk meg ennek megoldásával! Valahogy úgy, hogy a mátrixot több partícióra szétvágva, külön-külön Lótihoz rendeljük a rá vonatkozó műveletsort, amiket most már egymástól függetlenül, s főleg párhuzamosan végezhetnek el.
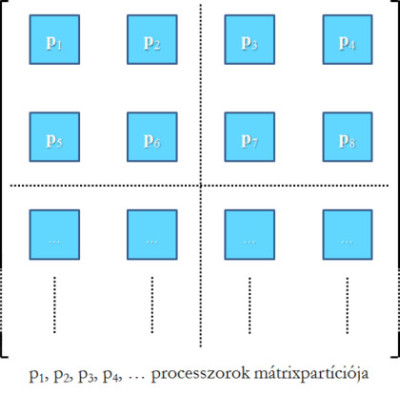 Processzorok mátrixa
Processzorok mátrixaLehet egy másik elképzelésünk a másik feladattípus esetére. Bár a lényeg megint a párhuzamos végrehajthatóság: Lótik mint futószalag mentén elhelyezkedő intelligens betanított munkások dolgoznak ugyanazon a feladaton. Ez a kalákaszerű munkaszervezés persze csak akkor hatékony, ha nagy mennyiségű adatra ugyanazt a bonyolult metódust kell alkalmazni. Ha egy képpel kell megvilágítani ezt a módszert, akkor egy olyan intelligens csövet kell magunk elé képzelni, amelyen helyenként kidudorodások vannak; a cső száján beöntve az adatokat, a cső dudorain átjutva és átalakulva a másik végén csöpög (vagy éppen hömpölyög) ki az eredményesszencia (illetve -folyam). (A Lóti Futik és háztartásuk egyébként hasonlónak mondhatók az eddig megismertekhez. Ami bonyolultabb az egyik és a másik esetben is: az összhang megteremtése, a kommunikációjuk megszervezése.)
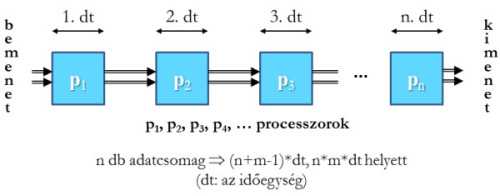 Processzorok futószalag mentén
Processzorok futószalag menténVégül egy harmadik elképzelés is adódik, ami talán a legkevésbé tűnik újszerűnek: több, önálló Lóti & Co. kapcsolatba hozása pl. közönséges telefonvonalon keresztül. Ekkor viszont a kommunikáció – amit az előbb eléggé kifejtetlenül hagytunk, az most – komoly problémává duzzadt, hiszen köztudomásúan zajosak és megbízhatatlanok a telefonvonalak. Gondoskodni kell az információ hibátlan, magabiztos célba jutásáról. Ehhez néhány, jól körülhatárolt feladatú szereplőre van szükség (aki a Lóti Futiék számjegyes [digitális] jeleit a telefonvonalakon szokásos folytonos [frekvenciamodulált, analóg] jelekké alakítja, majd vissza), és olyan kódolási módszerre, ami önmagában garantálja a hiba érzékelését, sőt javíthatóságát. Ez igen egyszerűen megvalósítható úgy, hogy pusztán ellenőrzési céllal plusz információkkal „hígítjuk föl” az átviendő anyagot. Például legkézenfekvőbb elképzelés: mindent kétszer küldeni. Ahol nem ugyanaz ismétlődött, ott hibának kell lennie...
Így tehát érzékelhető legalább a hiba (?). Ennél a gyanúsan kézenfekvő módszernél kitalálhatunk jobbat is, ami nemcsak az esetleges hiba tényét jelezheti, hanem azt is, hogy hol a hiba helye (hibák helyei), sőt miből torzult el az átvitel során. Alapgondolatul csak ennyit: kódolásra felhasználandó kódszámokat leszűkítjük; az így fölszabadultak csak rendellenes körülmények között képződhetnek. Ez teszi fölismerhetővé a hibát. A visszaállíthatóság érdekében, ezeknek a „kódlukaknak” az elhelyezkedését úgy választjuk meg, hogy a szokásos torzulások lehetőleg valamelyik nem megengedett kódhoz vezessenek. Ezzel reménykedhetünk abban, hogy nemcsak egyszeres hibákra, hanem kettő-, vagy többszörösre is rábukkanhatunk. Ára persze: a kód nagy redundanciája, azaz a hasznos és a tényleges kódszélesség arányának eltolódása. [CGDPKA]
A dolognak még csak az elején tartunk, hiszen az információáramlásnak csak a legalacsonyabb, fizikai szintjével foglalkoztunk. Hátra van még az abból a tényből fakadó problémák megoldása, hogy több, szuverén lótis társaság együttműködését kell megszerveznünk. Ilyen kérdésekre kell választ adnunk:
Ezért a fenti információkódolási módszert célszerű felfejleszteni egy speciális, kommunikációs célú nyelvvé, amelyben a kapcsolatfelvétel és -elbontás, az üzenetcímzés és az ismétléskérés mellett sok, az élet felvetette problémához van szókincse. Ezt a sajátos nyelvet (protokollt) – természetesen – egy külön e célra „teremtett” Teli Foni fogja ismerni, és beszélni. A dolog külön érdekessége az, hogy miként kapcsoljuk ún. hálózatba ezeket az individuális lótis háztartásokat. Valamilyen hierarchiába, vagy teljesen egyenrangúakként; mindenkit mindenkivel, vagy gyűrűsen csak a szomszédosakat összekötve (ez esetben is megvan a lehetőség a távolabbi szomszédokkal való kapcsolatteremtésre, így persze nem „első kézből” kapja az üzenetet).
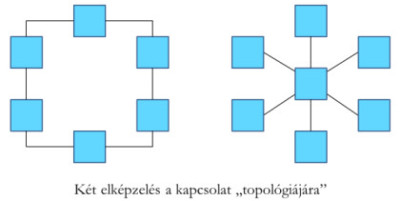 Hálózatban
HálózatbanSzót érdemel a hálózatban rejlő előnyök taglalása. Fölsorolunk néhányat – különösebb magyarázat nélkül – gondolatébresztőként:
A felvonásközi elmélkedés következik. A „tanulságok”:
1. A következő aritmetikai formuláknak felrajzolva a végrehajtási fáját elemezzük a párhuzamos kiszámítás szempontjából!
(A) 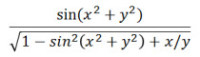
(B) A következőben a két kifejezés párhuzamosan számítandó ki!
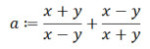
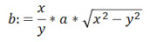
Figyelem: a (2)-ben az (1)-beli 'a' változó szerepel! Érdemes kiszámolni az effektív időnyereséget abból a feltevésből kiindulva, hogy pl. a +,– műveletek egy egységnyi idejűek, a *,/ három, a . ² (ti. négyzetre emelés) öt, az √ és a sin tíz, valamint az := (ti. az értékadás) három egységnyiek.
2. Érdemes elmélyedni a következő problémán. Nem ejtettünk ugyan külön szót arról, hogy a számítógép ókor-ókor hibázni is képes, de mindenki számára ez hihető. Adott egy olyan nagy horderejű feladat, amely megoldásánál nem tűrhető el az esetleges tévedés. (Közismert példákra utalva: repülőgép robotpilótáját megtestesítő számítógép, bankhálózat nyilván tartórendszere, vagy nukleáris erőmű vezérlőrendszere stb.) Készítsünk olyan lótis epizódot, amelynek kiinduló ötlete az, hogy a többprocesszoros rendszerben ugyanazt a programot ugyanazon adatokon párhuzamosan mindegyik processzor elvégzi a biztonság kedvéért, és egy ellenőrző mechanizmus dönt a fölmerülő vitás helyzetekben! (Ezek az ún. hibatűrő rendszerek.)
  |
 |
 |
A tananyag az ELTESCORM keretrendszerrel készült