Ebben a szimulációs tananyagban a szimuláció természettudományokban, illetve ezen tudományok oktatásában való alkalmazásával foglalkozunk. Ez a lecke általános ismereteket tartalmaz. Foglalkozunk benne:
Az oktatásban és a kutatásban nagyon sok jó tapasztalat gyűlt össze a kísérletezés, a személyes élmény megszerzésének hasznosságáról. Sok olyan terület van azonban, ahol ez nem lehetséges, a kísérlet nem végezhető el, mert:
Ezekben az esetekben tud segítséget nyújtani a számítógép (főleg az ún. személyi számítógép), mint univerzális kísérleti eszköz. Segítségével visszaadható a kísérletezés izgalmassága, élménye, nagy mértékben gyorsítható az adott jelenség megértése.
Az ezeken a területeken való hiánypótláson túlmutató lehetőség, hogy a számítógépet intelligens kísérlettervező eszköznek használjuk, segítségével gyorsan és hatékonyan megválaszthatók az elvégzendő kísérletek érdekesnek tűnő paraméterei, s ezek értékei. Nagyon fontos szerepe van így a számítógépnek az önálló alkotó munkára nevelésben, a kreativitás kifejlesztésében.
A számítógép ilyen célú felhasználásának más „haszna” is van, megmutatja azt, hogy a számítástechnika eredményei nagyon sokféle területen használhatók, a számítástechnika alkalmazását az alapműveltség részévé teheti.
A modell rendszerint bonyolult, részleteiben nem ismert fizikai, kémiai, biológiai stb. rendszerek működésének megismerésére készített sematikus elképzelés, amelyből új összefüggésekre lehet következtetni, vagy amely alkalmas arra, hogy a rendszer jelenségei matematikailag leírhatók legyenek. A modell a valódi rendszereknek többnyire csak főbb tulajdonságait tükrözi, egyszerűsített formában. Az, hogy melyek ezek a tulajdonságok, mindig attól függ, hogy miért van szükségünk a modellre.
A következőkben használjuk a modellezés és a szimuláció fogalmát, mindig aszerint, hogy milyen szempontból beszélünk a modellekről.
MODELLEZÉS: A modell elkészítésének folyamata.
SZIMULÁCIÓ: A modell használatának folyamata.
Általános szempontokból feladatmegoldó tevékenységünket három részre bonthatjuk, ezek:
A folyamatot egy feladat megoldásán keresztül mutatjuk be, a megoldást a szövegből kiemeljük:
Ez nagyon fontos tevékenység. Ez az, amely meghatározza további tevékenységeink célját, illetve döntően befolyásolja azoknak eredményességét, hatékonyságát. Meg kell adni azt a rendszert, amelynek vizsgálatával foglalkozunk, azokat a szempontokat, amelyeket fontosnak tartunk (paramétereket, illetve ezek értékhalmazait), és a várható eredményeket (hipotéziseinket a rendszer működéséről).
Várható eredmények: az eredményekről pontos elképzeléseink persze csak bizonyos konkrét paraméterek esetén vannak (ezek megfigyeléseinkből származnak), így minimális elvárásunk, hogy ezen paraméterek esetén a modell is szolgáltassa ezeket az értékeket.
A fejezeteken keresztül egy konkrét feladatot is vizsgálunk, az erre vonatkozókat dőlten szedjük.
Probléma: hogyan töltik ki a molekulák a rendelkezésre álló teret, ha mozgásukat semmi sem korlátozza?
Kísérlet: Adott két egymás mellé helyezett doboz, közöttük ajtóval. Használni fogunk egy átlátszatlan gázt és levegőt. Kinyitjuk a két doboz közötti ajtót, és figyeljük a gázok eloszlását (pl. átlátszóságot vagy tömeget mérünk).
Eredmény: Azt várjuk, hogy a gáz a két dobozt – a kezdőeloszlástól függetlenül – egyenletesen fogja kitölteni.
Feladatok megoldásának, a valóság megismerésének többféle módszerét ismerjük, először ezeket tekintsük át!
1. Megfigyelés → Törvény- (szabály-) alkotás
Ez a legősibb megismerési stratégia, melyet már az ősember is „alkalmazott”, lényege abban áll, hogy azt fogadjuk el szabálynak, ami már „sokszor bekövetkezett”. (Ilyen volt „A Nap minden nap felkel.” szabály.) Ez a törvényalkotás ma is elfogadottnak tekinthető, sok megfigyelési eredményből indukció útján hozunk létre új törvényeket.
2. Megfigyelés → Hipotéziskészítés → Megfigyelés → Törvény- (szabály-) alkotás
A megismerési folyamat itt azzal bővült, hogy kezdeti megfigyeléseink alapján a valós rendszer viselkedésére, állapotára stb. vonatkozó hipotéziseket állítunk fel, majd úgy végzünk további megfigyeléseket, hogy ezt a hipotézist elfogadni vagy elvetni tudjuk (felbukkan a valóság megismerhetőségének fogalma, a célirányos vizsgálódás lehetősége). A hipotézisalkotás két fontos gondolaton alapul, az egyik a természetre vonatkozó kérdések és a kérdésre adandó válaszok önálló megjelenése (a görög tudomány eredménye, kb. az i.e. VI. század körül – a matematika és a természettudományok [fizika] összekapcsolása, a fizika kvantitatív tárgyalásmódja), a másik az absztrakció tudatos alkalmazása. Az absztrakció a jelenség olyan leegyszerűsítése, amely a jelenség alapvető jellegét nem változtatja meg, csupán elvonatkoztat tőle, az egyedi jellemzőket hagyja el, és ezen kívül kvantitatív tárgyalásra alkalmas.
3. Megfigyelés → Hipotéziskészítés → Kísérletek → Törvény- (szabály-) alkotás
Itt az újdonság a valós rendszerhez való aktív hozzáfordulás. Már nem hagyatkozunk a valós rendszerben esetlegesen végbemenő jelenségek megfigyelésére, hanem előidézzük azokat a körülményeket, amelyek esetén a valós rendszer viselkedéséből következtethetünk hipotéziseink igazságára. Az elv nagyon régi, megint visszamehetnénk az ősemberig, illetve az ókori tudományokig; széleskörű tudatos, tudományos alkalmazásáról azonban csak a XVII. századtól beszélhetünk (Galilei tevékenységét emelhetjük ki példaként). Ugyancsak a XVII. század vívmánya az elméletek valósághoz való kötése szükségességének felismerése. Ez azt jelenti, hogy a törvények megalkotásánál a valóságból kell kiindulni, a megalkotott törvényeknek pedig alkalmazhatónak kell lenniük a valóságra. A XX. század újdonsága ezzel kapcsolatban az, hogy az elméletnek, a törvényeknek gyakorlati haszonnal is kell járnia.
4. Megfigyelés → Hipotéziskészítés → Modellkészítés (ha még nem létezik) → Kísérletek a modellel (szimuláció) → Törvény- (szabály-) alkotás
E megismerési módszer szerint a valós rendszer helyett annak csak mindig egy mását, hozzá valamennyire hasonló rendszert vizsgálunk, és ennek viselkedéséből következtetünk az eredeti rendszer viselkedésére. Modellek készítése szintén nem új „találmány”, minden bizonnyal az ősember is készített modellt, itt azonban a modell nemcsak a valóság szótlan mása volt, hanem valamilyen visszahatást is feltételeztek a modellből a természetre; neves fizikusunk szavaival élve „az absztrakt nyíllal megölt absztrakt bölény elősegíti az igazi bölény igazi nyíllal való elejtését”. Az ókori görögök is használtak modelleket, sőt ezt a használatot elég gyakran „túlzásba is vitték”, melynek csúcsa volt talán a Püthagoraszi számmisztika vagy Zénón híres apóriája (paradoxona) a teknősről, amelyet a leggyorsabb futó (Akhilleusz) sem tud utolérni. A modellek ilyen vizsgálatában az volt a hiba, hogy a modellből kapott eredményeket nem, vagy nagyon hiányosan vetették össze a tapasztalattal (ha egyáltalán hajlandóak voltak a tapasztalat talajára leereszkedni), sőt a modelleket a valóságtól szinte függetlenül hozták létre. Arkhimédész a maga alkalmazott tudományával szinte kivételnek számított, egyébként általában „vigyáztak” nehogy eredményeiknek gyakorlati alkalmazása legyen, a modellt, a hozzá kapcsolódó logikát tekintették elsődlegesnek.
Megemlíthető érdekességként, hogy a modell megelőzheti a tapasztalatot (egy modellkísérletből származik például az elemi részecskék kvark-modellje). Erre akkor van lehetőség, ha a modell segítségével a valóság magyarázható, de természetesen a modell ilyenkor lehet hamis is (az, hogy magyarázható vele a valóság, még nem a jóság bizonyítéka; ha nem magyarázható, akkor viszont biztosan hibás).
A modern „modellmódszer” azonban nagyon szorosan kapcsolódik a valósághoz, ezzel a kapcsolattal a továbbiakban még foglalkozunk. Az első használható és sikeres modelleket a fizikában alkották meg, ilyen volt az ideális gáz, a tökéletes folyadék, a kiterjedés nélküli tömegpont, a matematikai inga, az atommodellek stb. A fizikát csak sokkal később követte a kémia, a biológia, a földtudományok.
5. Tapasztalatok gyűjtése megfigyelésekkel Modell alkotása tapasztalataink megértéséhez Jóslás a modell segítségével még nem ismert jelenségeket A jóslás helyességét kísérlettel ellenőrizzük, közben megállapítjuk a modell érvényességi határát Gyakorlati feladatok megoldása a modell segítségével az érvényességi határon belül Az érvényességi határon túli jelenségek magyarázatához a modell továbbfejlesztése, módosítása, esetleg teljesen új modell kidolgozása
Nézzük meg részletesebben az utolsó megismerési módszert!
Tevékenységünket a következő, objektumokból és rajtuk végzett műveletekből, tevékenységekből álló folyamat jellemzi:
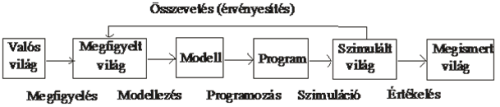A modellezés folyamata.Általános értelemben szokták ezt az egész folyamatot is szimulációnak nevezni.
Tevékenységünk minden lépésében meg kell győződnünk, hogy az éppen létrehozott objektum tulajdonságai megfelelnek-e annak, amelyből készítettük (így pl. a program rendelkezik-e azokkal a tulajdonságokkal, amelyeket a modelltől elvártunk), illetve az egyes objektumok önmagukban való helyességükről. A végső döntést az összevetés (vagy érvényesítés) során hozzuk, ekkor tudjuk egész tevékenységünket értékelni. Amennyiben a szimuláció eredményei megfelelnek várakozásainknak, akkor célunkat elértük; ha nem, akkor meg kell vizsgálni, hogy tevékenységünk melyik lépésében hibáztunk, majd ezt kijavítva, és a javítást a későbbi tevékenységekben is elvégezve, újra elkészítjük a fenti objektumokat.
Mielőtt részletesebben megvizsgálnánk az ábra egyes tevékenységeit, tekintsük át a modellek lehetséges osztályozásait!
A modelleket sokféle szempont szerint csoportosíthatjuk, itt néhányat (a fontosabbakat) bemutatunk ezek közül [SzE]:
1. A modell használatának célja:
Nekünk elsősorban a második és a harmadik cél fontos.
2. A modellezett jellege:
Itt a csoportosítás arra vonatkozik, amit modellezünk.
3. A modell jellege:
Itt a csoportosítás arra vonatkozik, amivel modellezünk.
4. A modellezési szempont:
Vagyis miben hasonló a modell a modellezetthez, mi az, ami a modellezés alapjául szolgál?
5. A modell változói szerinti osztályozása:
Rendszerelmélet szerinti közelítésben a rendszer háromféle rendszerelemet tartalmazhat: bemenő változót (paraméter), állapotváltozót és kimenő változót. Ezek alapján három csoportosítási szempont szokásos:
A: Emlékezet nélküli modell: nincs állapotváltozója, nincs amiben „nyomot hagyhatna” a ráhatás.
Emlékezettel bíró modell: van állapotváltozója.
B: Autonóm modell: nincs bemenő változója, független a külvilágtól, nem hatnak rá annak változásai.
Nem autonóm modell: van bemenő változója.
C: Zárt rendszer modell: csak állapotváltozója van.
Nyílt rendszer modell: van vagy bemenő, vagy kimenő változója, vagy mindkettő.
A csoportosítást végezhetjük a változók értékkészlete alapján:
A: Diszkrét állapotú modell: minden változója csak diszkrét értéket vehet fel.
B: Folytonos állapotú modell: változói csak folytonos értékeket vehetnek fel.
C: Kevert állapotú modell: van mind diszkrét, mind folytonos értéket felvevő változója is.
A csoportosítást végezhetjük a változók időfüggése alapján:
A: Időfüggő modell: legalább egy változó értéke függ az aktuális időtől, a modell jellemzője, hogy az egyes eseményei nem ismételhetők meg. (Például gyümölcsfák virágzása csak tavasszal történhet meg.)
B: Időfüggetlen modell (stacionárius): a T=0 időpont tetszőlegesen megválasztható, eseményei általában megismételhetők.
Két fajtája különböztethető meg:
B1: Statikus modell: az idő nem szerepel a modellben, nincs változás (azaz az eredményt egyszer, s mindenkorra meghatározza).
B2: Dinamikus modell: a modellben változások lépnek fel, az időnek szerepe van.
6. A szimuláció időkezelése szerinti osztályozás:
A: Diszkrét idejű modell: a változói diszkrét időközönként változnak.
B: Folytonos idejű modell: a változói folyamatosan változnak (számítógépek esetén ezt diszkrét változással közelítjük).
7. Az eredményváltozók függősége szerinti osztályozás:
A csoportosítást végezhetjük a modell determináltsága alapján:
A: Determinisztikus modell: a bemenete és a kezdőállapota egyértelműen meghatározza az eredményt.
B: Sztochasztikus modell: a bemenete és a kezdőállapota csupán az eredmény lehetséges értékeinek eloszlását határozza meg (sőt van olyan, ami csak annyit közöl, hogy milyen értékeket vehet föl egy-egy rögzített bemenet, illetve kezdőállapot esetén, de ennek eloszlását már nem).
További csoportosítás szempontja lehet, hogy a modell viselkedése függ-e a jövőtől:
A: Nem előrelátó modell: változása nem függ a jövőtől.
B: Viselkedésében előrelátó modell: bizonyos állapotaiban nagy valószínűséggel előreláthatók következő állapotai vagy bemenetei (és ezt fel is használja).
További csoportosítás szempontja lehet, hogy a modell viselkedése a jelenben függ-e a múlttól:
A: Emlékezet nélküli modell: a modell viselkedése csak a külső hatásoktól függ, azonos hatásra mindig ugyanúgy reagál.
B: Utóhatás mentes modell: a modell viselkedése az utolsó állapottól és a külső hatásoktól függ, vagyis mindegy, hogy hogyan jutott az adott (belső) állapotba.
C: Teljesen függő modell: a modell viselkedése a teljes múlttól függ: a következő állapotának meghatározásában az összes múltbeli „emlék” szerepet játszik.
A következőkben részletesen megvizsgáljuk a szimulációs folyamat egyes tevékenységeit.
Az információszerzés egyik lehetséges módszere a megfigyelés. Ilyenkor a lejátszódó folyamatról akarunk ismeretet szerezni. Mit figyelhetünk meg? Megfigyelhetjük a természetben lejátszódó folyamatokat, mint pl. a madarak vándorlási irányait, a tengeráramlatok hatását az időjárásra, a légkör szennyezettségét stb. Ezek nagyon hasznos ismereteket szolgáltathatnak, de közvetlen módon általában nem befolyásolhatjuk őket, vagy nagyon hosszú időnek kell ahhoz eltelnie, hogy a beavatkozás hatását érdemben észleljük. Azért ilyenre is van már több példa, ilyenek a jégrakéták, amik a jégverés megakadályozását szolgálják. Ennek megkonstruálását a jégesőfelhők tulajdonságainak megfigyelése tette lehetővé. De megfigyelhetünk egy gyártási folyamatot is. Elvárásaink szerint játszódik-e le a folyamat: a gyártmányok milyen paraméterűek, megfelelnek-e az előírtaknak stb. A megfigyelés természetesen mérésekben realizálódik. Ezen mérések feldolgozása – méréskiértékelés – teszi lehetővé a lejátszódó folyamat mind pontosabb megismerését, a beavatkozás módját.
A megfigyelés lényege tehát a valós rendszerből azon adatok megszerzése, összefüggések felismerése, amelyek a rendszerre a vizsgálat szempontjából jellemzőek. A „megfigyelt világ”-on a hagyományosan adatnak nevezett objektumokat értjük, és a közöttük fennálló összefüggéseket is (tulajdonképpen a valós rendszerről való összes lényegesnek tartott tudásunkat).
Csoportosítsuk aszerint a megfigyeléseinket, hogy a nyert adatokat mire használhatjuk!
Ezek segítségével pontosabban írhatjuk le környezetünket. Gondoljunk csak a relativitás, mint fogalom megszületésére! Mérhetetlenül sok és aprólékosan gyűjtött, ellenőrzött adat kellett ennek megfogalmazásához, és az erre épülő relativisztikus mechanika kidolgozásához. A megfigyelések sokasága vezetett annak a téveszmének módosításához is, amely szerint a Föld a mindenség központja, azaz a geocentrikus világkép megdöntéséhez. (Bár körmönfont módosításokkal – hiperciklusok bevezetésével – a geocentrikus modellt igazítani lehetett a megfigyelésekhez, a természet azonban az egyszerűbbet részesítette előnyben, rácáfolva az embercentrikus felfogásra.)
Gondoljunk pl. egy gyógyszergyárra ahol állandóan mérni kell a gyógyszerek összetételét az esetleges hibák – „elmérések”, gondatlanság – elkerülésének érdekében. Vagy gondoljunk pl. egy olyan üzemre, ahol meghatározott méretű alkatrészeket kell gyártani. A selejtet csökkentendő, bizonyos időközönként mintát veszünk a kész darabokból, ellenőrizzük azokat és szükség esetén átállítjuk a szerszámokat, esetleg újra cseréljük azokat. Ezek tehát mind mintavételen alapulnak. Ezen minták kiértékelése után avatkozhatunk csak közvetlenül a folyamatba.
Egy fejlettebb változata a mérések kiértékelésének az az esete, amikor közvetlen vezérlésre használjuk a szerzett adatokat. Példának vegyük a távfűtés vagy mondjuk a melegvíz-szolgáltatás esetét. Ha a víz hőmérséklete egy adott érték fölé emelkedik, automatikusan kikapcsoltathatjuk a kazánt. Tekintsük a közlekedésirányítás azon fejlettebb módszerét, amikor a közlekedési lámpák a forgalomtól függően irányítják a forgalmat. Ezt nyilván úgy végzik, hogy valamilyen módon regisztrálják az időegységenként áthaladó járművek számát. A riasztóberendezések szintén hasonló elven működnek. Fontos motiváló tényezője a vezérlésnek a baleset-megelőzés. Az első példánál maradva, ha a kazán túlmelegedne, a robbanás megelőzése érdekében szintén leállíttatjuk.
Ahhoz, hogy megfigyeléseket (méréseket) végezhessünk, már ismerni kell sok mindent a valós rendszerről, ismerni kell az alapvető törvényeket, el kell dönteni, hogy mit és hogyan mérjünk stb. A megfigyelés hatása messzire terjed, ugyanis a megfigyeléseket megváltoztatva, a valóságnak egészen más modelljét kaphatjuk, így más következtetéseket vonhatunk le az eredményekből. A legfontosabb kérdés a megfigyelésekkel kapcsolatban az, hogy
„Mit figyeljünk meg?”
Ezzel kapcsolatban első feladatunk a rendszer belső szerkezetének megismerése (természetesen csak azon szempontok alapján, amelyek fontosak a feladat szempontjából). A modell létrehozásakor ebből indulunk ki. Itt meg kell ismerni a rendszer egyes összetevőit, ezek kapcsolatát, a rendszerben létező hatásokat és azok súlyát. Azonosítani kell a külső hatóerőket, melyeket a továbbiakban a rendszer változóinak, paramétereinek tekintünk. Súlyos probléma, hogy ezek a paraméterek általában nem függetlenek egymástól és így nem választható kísérleti paraméternek tetszőleges kombinációjuk. Ez később, az eredmények értékelése során is gondot okozhat. Például a kapott regressziós együtthatók nem fejezik ki a valódi függést (a megfelelő egyenletrendszer ugyanis nem oldható meg egyértelműen), a korrelációs együtthatók sorrendbe állításával nem választhatók ki a legfontosabb hatóerők (ugyanis ugyanazt többször is beszámíthatjuk szándékunk – és tudomásunk – ellenére) stb. A változók hatásait ezért független, hipotetikus változókba (ún. faktorokba) sűrítjük, melyek száma általában lényegesen kisebb az eredeti változók számánál. Erre a feladatra a faktoranalízis módszerei szolgálnak. Ezután el kell dönteni, hogy
„A rendszerből mennyi paramétert figyeljünk meg?” és
„Melyek legyenek ezek?”
Ez nagyon nehéz probléma, ugyanis minél több paramétert veszünk figyelembe, annál pontosabb lesz a valóságról alkotott képünk, viszont annál nehezebb lesz az összefüggések felismerése, illetve jelentősen növekedhet a szükséges, elvégzendő kísérletek száma. A legegyszerűbb esetben két paramétert figyelünk meg, az egyik állapotából következtetünk a másikra (általában a második valamilyen függvénye az elsőnek és mi ezt a függvénykapcsolatot szeretnénk megismerni). Bonyolódik a feladat, ha az ismert változók száma nagyobb: ekkor már többváltozós függvények felismeréséről van szó. Ilyen esetben legtöbbször az egyetlen jó hatékonyságú (absztrakt, matematikai) módszer a szimuláció. Ekkor sem célszerű nagyon sok paramétert használni, nehéz jó felső határt mondani a számukra, de általában ötnél csak akkor használjunk többet, ha hatásuk részben ismert, vagy tudjuk, hogy valamilyen egyszerű kapcsolatban vannak. El kell dönteni, hogy
„Az összes lehetséges paraméter közül melyeket fogjuk vizsgálni?”
Első megállapításunk az lehet, hogy azokat, amelyek a feladat szempontjából fontosak. Ezt a fontosságot tudhatjuk a feladat kitűzéséből, korábbi ismereteinkből, ha azonban ezt nem tudjuk (vagy nem biztosan tudjuk), akkor valamilyen módszert kell keresni a paraméterek rangsorának megállapítására. Erre a célra használható a változók (illetve a már független faktorok) az eredménnyel való korrelációs együtthatók szerinti sorba rendezése. Ez a módszer használható egyben a figyelembe veendő paraméterek számának meghatározására is, lényege az, hogy a változókat ott választjuk szét két csoportra, ahol a sorba rendezett korrelációs együtthatók között nagy csökkenést tapasztalunk.
Már a feladat kitűzésekor eldöntöttük, hogy a gáz eloszlását fogjuk megfigyelni az ajtó kinyitása után. Ekkor egyszerű esetekben itt más dolgunk nincs.
A másik fontos probléma az, hogy
„Az összes lehetséges megfigyelésből melyeket végezzük el?”
Melyik megfigyelések kerüljenek a mintába (az elvégzett megfigyelések közé)? Ehhez tekintsük át a mintavétel lehetséges módszereit!
Az egyes megfigyeléseknek függetleneknek kell lenniük egymástól. Vigyázni kell, hogy az egyes mérési eredmények ne befolyásolják a következőket! (A következőkben egyszerű, feltűnően rossz példákat mutatunk be, amelyekkel a mintavétel hibalehetőségeire szeretnénk felhívni a figyelmet.)
Nagyon rossz módszer egy populáció megfigyelésére az, ha mindig ugyanazt az egy egyedet figyeljük meg.
A megfigyeléseket úgy kell végezni, hogy azok lehetőleg ne befolyásolják a vizsgált rendszert!
Nagyon rossz módszer egy vadon élő állat viselkedésének megfigyelésére az, ha az állatot egy ketrecbe zárjuk, és ott végezzük el a megfigyelést (hacsak nem ez a megfigyelés célja).
Biztosítani kell továbbá az azonos körülményeket a figyelembe nem vett hatóerőkre, illetve a figyelembe vettekre is, ha fontos a mintaelemek azonos eloszlása! A figyelembe nem vett hatóerők (lehetőség szerint) ne befolyásolják megfigyeléseinket!
Nagyon rossz módszer egy virág színének megfigyelésére az, ha a megfigyeléseket mindig sötétben végezzük el.
Hibás dolog azonban olyan következtetéseket levonni belőlük, amelyekre a megfigyelések nem vonatkoznak.
Az éjszakai bogarakról nem beszélhetünk nappali megfigyelések alapján, de úgy sem hogy a megfigyelést mindig ugyanabban az időpontban végezzük, például éjfélkor (hacsak nem ez a kérdés).
Mintavételi módszereinket két csoportra oszthatjuk (mindkettő a matematikai statisztika általános módszereit tartalmazza):
Ha a megfigyelt rendszernek véges sok állapota van, akkor úgy kell mintát választani belőle, hogy mindegyik állapot azonos valószínűséggel kerüljön bele a mintába!
Adott N db lehetséges elem (állapot, egyed stb.). Ezekből véletlenszerűen válasszunk ki M darabot! Itt csupán azzal kell törődni, hogy az egyes elemek egyenlő valószínűséggel kerüljenek a mintába. A módszer nagy problémája az, hogy előre nagyon ritkán tudjuk megmondani, hogy hány megfigyelésre van szükségünk. A tapasztalat azt mutatja, hogy gyakran sokkal több mintaelemet választunk, mint amennyire ténylegesen szükségünk lenne. A minta szükséges elemszámát matematikai módszerekkel becsülhetjük.
Adott N db. lehetséges elem, ezekből véletlenszerűen válasszunk ki M1 darabot! Ha ebből kielégítő eredményt kapunk (a modellünket el tudjuk készíteni és használata során a valóságnak megfelelő, magyarázható eredményeket kapunk), akkor készen vagyunk; ha nem, akkor válasszunk ki további M2 darabot, s az így kapott M1+M2 elemű mintát használjuk a továbbiakban!
Ez a módszer kiküszöböli a fent említett hibát, sokszor azonban nem gazdaságos. Ha a megfigyelések megkezdése előtt például nagyon költséges, vagy bonyolult, hosszú előkészületeket igényel, akkor az előbbi módszer jobb, bár esetleg több megfigyelést kell elvégezni.
Adott N db. lehetséges elem, addig vegyünk egyesével új mintaelemeket, amíg nem kapunk kielégítő eredményt!
Kielégítő eredmény: a mintából számított tapasztalati szórásnégyzet, konfidencia intervallum stb. kicsi.
Látható, hogy ez a módszer az előbbi gondolat (több mintavétel) szélsőséges esete, így ennek segítségével lehet a legkisebb elemszámú mintát kiválasztani, és ha egy megfigyelés költséges, akkor ez valóban nagyon gazdaságos módszer. Előnye továbbá, hogy előre nem kell meghatározni, hogy milyen elemszámú legyen a mintánk. A gyakorlatban ezt a módszert mégis úgy érdemes használni, hogy lépésenként 6-8 megfigyelést végzünk.
A mintavétel megbízhatóságának növelése érdekében, szóráscsökkentés céljából ún. rétegezést végezhetünk. A rétegezés lényege az, hogy a vizsgálat szempontjából sokféle rendszerállapotot egymáshoz hasonló állapotok osztályaiba csoportosítjuk. Ezek után mindegyikben elvégzünk egy egyszerű mintavételt. Fel kell használnunk ezen rétegek súlyát a rendszerben (ez lényeges többletinformációt feltételez), a megfigyelt értékek súlyozott összege (halmaza) lesz jellemző az egész rendszerre. Ezzel a módszerrel elkerülhetjük azt a lehetőséget, hogy egy kis elemszámú, de szignifikánsan (jelentősen) eltérő jellemzőjű halmazból nem veszünk mintaelemeket, illetve nem a rendszerbeli arányának megfelelő mennyiségűt veszünk. Magától értetődően a kulcsproblémát az jelenti a módszernél, hogy hol húzzuk meg a réteghatárokat. Sokszor előfordulhat, hogy a mintavétel előtt nem tudjuk, hogy egy elem melyik rétegbe tartozhat. A mintavétel utáni rétegezés ebben az esetben is előnyös lehet a rétegek súlyának ismeretében.
Rétegek súlya: a rétegbe tartozó elemek száma osztva a teljes rendszer elemeinek számával.
A csoportos mintavétel lényege, hogy a megfigyelt rendszerünkből először nem mintaelemeket választunk, hanem mintacsoportokat. Ezután vagy a kiválasztott mintacsoportok összes elemét mintaelemnek tekintjük, vagy a mintacsoportokból újabb választással mintaelemeket határozunk meg.
Akkor alkalmazható, ha a megfigyelt rendszer részrendszerekből áll. Lehetséges esetei (első esetben a részrendszerek azonos eloszlásúak, a másodikban pedig azonos típusú elemekből állnak):
Egylépéses mintavétel
Kiválasztunk véletlenszerűen egy vagy több csoportot, majd ezek minden elemét belevesszük a mintába. Ezt a módszert gyakran használják minőségellenőrzésnél, pl. egy almaszállítmánynál felbontanak néhány ládát, és a bennük levő almák minőségéből következtetnek az egész minőségére. Annak megválasztását, hogy hány csoportot kell végignézni ahhoz, hogy az egészről „meggyőzően” mondhassunk valamit, matematikai statisztikai módszerekkel végezhetjük.
Kétlépéses mintavétel
Kiválasztunk véletlenszerűen egy vagy több csoportot, vagy esetleg az összeset, majd mindegyik csoportból választunk véletlenszerűen egy vagy több elemet. A csoportokból való választásoknak egymástól függetleneknek kell lenniük.
Abban az esetben használjuk őket, ha a megfigyelt rendszernek végtelen sok állapota van, végtelen sok lehetséges megfigyelésből kell kiválasztani egy mintát. A módszerek közös tulajdonsága az, hogy az n-dimenziós megfigyelési térre egy n-dimenziós (véges) rácsot fektetünk, majd a rácspontokból választunk mintaelemeket (ezek már véges sokan vannak). Lehetséges módszer az összes rácspont kiválasztása, rácspontok véletlenszerű kiválasztása, bizonyos rácspontok által határolt hiperkockák (n-dimenziós kockák) további felosztása újabb rácsokkal stb.
N-dimenziós megfigyelési tér: N db változót (paramétert, jellemzőt stb.) tartalmaz.
Az eddigi mintavételi módoknál betartottuk azt a szabályt, hogy mintaelemeket egyenlő valószínűséggel választottunk a lehetséges mintaelemek közül. Végezhetünk ún. fontosság szerinti mintavételt is, ilyenkor azonban a mintavétel okozta torzítások megszüntetéséről gondoskodni kell.
Rendszerünk véges, de rendkívül nagyszámú állapota van (az első dobozban 0, 1, 2, gázmolekula található), így a rácsmódszerekhez folyamodunk. Mivel egyetlen paramétert kell megfigyelnünk, ezért egydimenziós rácsot használunk, a sok lehetséges értékből kiválasztunk néhány jellemzőt.
Kezdőeloszlások:
Következtetés: Úgy tűnik, hogy a kezdőeloszlástól függetlenül, egy idő után a gázmolekulák nagyjából egyenletesen oszlanak el a két dobozban.
Az előbb vázoltak fontos jellemzője volt, hogy ismertük a lejátszódó folyamatot. Információigényünk szinte csak arra korlátozódott, hogy a folyamatot „kordában” tartsuk, megfelelően módosíthassuk, amennyiben az szükségessé válik.
Ha csupán a „passzív” megfigyelések nem szolgáltatnak elég ismeretet, akkor ezt kísérletekkel kell „kicsikarnunk” a vizsgált rendszerből. A kísérleteket – a cél szempontjából – két nagy osztályba sorolhatjuk.
Ha nem ismerjük a lejátszódó folyamat összefüggéseit, akkor kísérleteket végzünk és megpróbálunk következtetni a folyamat modelljére, összefüggéseire. Ezek nem feltétlenül célirányúak. Ezeket ne is nevezzük kísérleteknek, nevezzük inkább „felfedezésnek”. Gondoljunk Arkhimédészre, aki – a legenda szerint – fürdés közben jött rá híres törvényére, vagy Newtonra, akinek „a fejére esett az alma”, vagy a kukta föltalálójára, akit idegesített, hogy főzés közben a gőz emelgeti a födőt, ezért lekötözte azt, s így – mellesleg – hamarabb lett kész az étel. Viszont nyilvánvalóan célirányúak voltak az űrrepülést előkészítő földi kísérletek, vagy a belsőégésű motorok feltalálását előkészítő kísérletek, vagy gondoljunk a C-vitamin előállítását megelőző nagyon fontos kísérletekre stb. Ezek a roppant nagy jelentőségű találmányok természetesen egy-egy kiemelkedő elme gyakorlati tapasztalatainak és elméleti tudásának köszönhetően születhettek meg. Ezeknél persze vannak sokkal „prózaibb”, a mindennapi élethez tartozó kísérletek is, így pl. a kutató-, fejlesztő-laboratóriumokban újabb és újabb hatékony gyógyszerek kifejlesztésén dolgoznak, kísérleteket végeznek az ólommentes benzin minél olcsóbb előállítására, az elektromos autó minél hosszabb idejű üzemben tartásra, a kártevőknek és a szárazságnak fokozottan ellenálló haszonnövények nemesítésére, minél jobb paraméterű – tejhozam, tojáshozam növelése – haszonállatok kitenyésztésére stb. Ezek a kísérletek persze sokszor zsákutcába is vezethetnek, de így is hasznosak lehetnek, mivel az ilyen eseteket kizárhatjuk az elkövetkezendő vizsgálataink sorából.
A lejátszódó folyamat összefüggéseit ismerjük ugyan, de más és más környezetben vizsgáljuk. Gondoljunk például a nehézségi gyorsulásra. Ismeretes, hogy ennek értéke más a sarkokon és más az egyenlítőnél. Kísérleteket végezhetünk ennek minél pontosabb meghatározására. Vagy ismerjük egy guruló test lejtőn való mozgásának energiaviszonyait. Vizsgálhatjuk a veszteség függését a mozgás különböző paramétereitől. Mivel a folyamatokat leíró matematikai modellek általában idealizáltak – pl. eltekintenek a közegellenállástól, nem veszik figyelembe a gördülő súrlódást stb. – ezért ezek a mérések igen fontos szerepet játszanak a gyakorlati, technológiai módszerek kidolgozásában.
Modellezéskor a megfigyelt adatok felhasználásával olyan – általában matematikai – módszerekkel írjuk le a rendszert, melyek segítségével a valós rendszer tulajdonságaira következtethetünk, annak viselkedését előre láthatjuk. Ilyen formalizmusra számos példa létezik (közönséges differenciálegyenletek, parciális differenciálegyenletek, differenciaegyenletek, véges állapotú automaták, Markov-láncok, folyamat kölcsönhatáson alapuló módszerek, formális rendszerek – Lindenmayer, sejtautomaták stb.); ezek azonban bonyolult matematikai apparátust igényelnek, így használatuktól mi általában eltekintünk. Formalizmusunkban egy funkcionális (működés megadáson alapuló, algoritmikus) leírási forma (amit programozási célokra is használunk) használatát fogjuk követni, amely során néha matematikai (főként valószínűségszámítási) megfontolásokat is kell tennünk.
A modell önmagában sohasem lehet a modellezés célja, hanem mindig a modellezett vizsgálatára kell, hogy alkalmas legyen, ezért a modellnek mindig „működőképesnek” kell lennie. Mielőtt a következő tevékenységbe kezdenénk, meg kell győződni arról, hogy a modell megfelel céljainknak. Ha valamilyen matematikai módszert használtunk, akkor a feladat matematikai megoldását, esetleg részmegoldását elvégezve meg kell vizsgálnunk, hogy a várt eredményt kapjuk-e (ezért volt fontos a feladat kitűzésekor az elvárható eredmények megadása).
Ha a modellünk szemléltetési céllal készül, akkor a szemléltetés érdekében megengedhetők a modell belső felépítésére olyan kapcsolatok, amelyek a valódi jelenségben esetleg ilyen formán biztosan nincsenek, mert ilyenkor csak az eredmény a fontos! (Természetesen e kapcsolatok nem érinthetik a modell működésének lényegi mechanizmusát, azaz rossz képzeteket nem sugallhatnak.) Ha a modellünk célja valamilyen elemzés, akkor a modellt a valós rendszerre vonatkozó feltevéseink alapján kell elkészíteni, és ilyenkor óvakodni kell a „káros analógiáktól” (így született többek között a horror vacui fogalma: amely szerint a testek az űrtől való idegenkedés miatt esnek mindig lefelé)!
A modell megalkotása előtt megfigyelésekkel ismereteket szereztünk, hipotéziseket állítottunk fel a modellezett rendszerben létező objektumokról, ezek kapcsolatairól, állapotairól, változásairól, a külső hatóerőkről, a modellezett rendszer állapotairól.
A szokásos matematikai modellek megalkotása ebben a helyzetben a rendszer paraméterei, állapotváltozói közötti matematikai összefüggés meghatározását jelenti, a konstruktív módszereknél azonban más – könnyebb – úton is járhatunk.
A modellalkotás első lépésében meg kell határozni a modellben szereplő – absztrakt – objektumokat, amelyeket meg kell feleltetni a valós rendszer objektumainak (illetve objektumai egy-egy osztályának). Ez a megfeleltetés általában állapotaik megfeleltetését jelenti. Ahhoz ugyanis, hogy objektumokról külön-külön beszélhessünk (ahogyan a valós rendszerben), szükség van individuális létezésükre, amelyet állapotaik megadásával helyettesítünk. Ezután következő feladat a rendszer állapotváltozását (az objektumok számának változását, állapotainak változását) leíró algoritmus elkészítése.
A matematikai modellek készítésével szembeni lényeges különbség abban van, hogy így nem a már úgyis komoly absztrakciós tevékenység során nyert – matematikai – változók között kell valamilyen matematikai kapcsolatot találni (amely újabb absztrakciós lépés eredménye), hanem a sokkal könnyebben megfogható valós rendszerbeli valódi kapcsolatok „lemásolása” a feladat. További különbség, hogy a modell így megőrzi a valós rendszer dinamikus struktúráját, eseményeit, természetességét. Útmutatónk az eredeti jelenség lesz, módszerünk pedig a jelenség valósághű lejátszása.
Modellkészítéskor nagyon sokszor felmerülő probléma megfigyeléseink hiányossága, pontatlansága, sokszor nem kellő céltudatossága. Ez minden esetben elkerülhetetlen akadályt jelent, így egy kicsit foglalkoznunk kell vele. Ha ezekről a hiányosságokról, pontatlanságokról nem veszünk tudomást, azzal nagy kárt okozhatunk magunknak, s ha a modellel nem csak szemléltetési céljaink vannak, akkor másoknak is. Gondoljunk például kényes egyensúlyú ökológiai rendszerekre; kicsit erős hasonlattal élve: egy ilyen hiba például a Balaton teljes élővilágának kipusztulásához is vezethetne.
Ha egy hatóerőről semmit nem tudunk, akkor nem sok reményünk van arra, hogy a modellünkben figyelembe vehessük; a gyakorlatban azonban legtöbbször nem ilyennel van dolgunk. Általában ismerjük az egyes hatások átlagos értékét, szórását, eloszlását és ennek alapján több reményünk van a modell helyes elkészítésére. Ilyenkor sztochasztikus modellt fogunk kapni, s nagyon sok modellkísérlet elvégzésével sokkal megbízhatóbb képet szerezhetünk a valós rendszer viselkedéséről, stabilitásáról. Sztochasztikus modellek alkotása még abban az – egyébként nagyon ritka – esetben is előnyös lehet, ha a hatóerőket pontosan ismerjük (elég nagy pontossággal egy stabil rendszerben), amennyiben ezek a hatóerők nagyon sokan vannak. Tehát a valós rendszert az Y=F(X1,...,Xm) függvény helyett az Y=G(X1,...,Xk,P1,...,Pn) függvénnyel írjuk le, ahol k << m és a Pi értékeket véletlenszám-generátorral állítjuk elő. Ebben az esetben természetesen tudnunk kell valamit a közelítés jóságáról (jogosságáról). A módszer lényege az, hogy a változók egy részét csak hatásuk eredőjének egy statisztikus mennyiségével helyettesítjük. Sok hatás együttes vizsgálata megnehezíti a modellkészítést, a modellt túlságosan bonyolulttá, a vele való kísérletezést lassúvá teszi. Ilyenkor járható út a kevésbé fontos hatóerők eredőjének valamilyen statisztikus becslése, amellyel a figyelembe vehető változók számát lényegesen csökkenthetjük. Mindezek alapján mi a továbbiakban sztochasztikus modelleket fogunk készíteni. Természetesen mindegyikben fog szerepelni valamennyi determinisztikus elem is, illetve szélsőséges esetekben ezek fogják jelenteni a modell meghatározó részét.
Az algoritmus akkor írja le jól a valós rendszer működését, ha:
A valós rendszer objektumai: az egyes molekulák.
Állapotjelzőjük: az 1. , vagy a 2. dobozban vannak-e.
A modell objektumai:
N - a molekulák száma,
D(N) - az egyes molekulák „állapotai”
A - az 1. dobozban levő molekulák száma
Megfeleltetés:
D(i)=1, ha az i. molekula az 1. dobozban, D(i)=2, ha a 2.-ban van.
A változást leíró algoritmus: (a lényege)
Eljárás: i:=Véletlen(N) [1 és N közötti véletlen egész] Ha D(i)=1 akkor D(i):=2; A:=A-1 különben D(i):=1; A:=A+1 Eljárás vége.
A modell-modellezett kapcsolat hasonlóság, a modell mindig csak valamilyen szempontból hasonló a modellezetthez. Nagyon fontos ennek a hasonlóságnak a létezése, ez biztosítja ugyanis, hogy a modell állapotának ismeretében a modellezett állapotát meg tudjuk határozni (biztosan vagy nagy valószínűséggel – statisztikus modellek). „Teljes modell”, azaz olyan, amely minden szempontból hasonló a modellezetthez, csak egy van, maga a modellezett, így a hasonlósághoz mindig meg kell adni, hogy milyen tulajdonságokról van szó, milyen szempontból legyen a modell hasonló a modellezetthez. Előfordulhat azonban, hogy a modellezés csak nagyon durva közelítéssel valósítható meg, ami teljesen bizonytalanná teheti az eredmény használhatóságát, ilyenkor a modellezés csak akkor végezhető el, ha az eredmény helyességét más módon is tudjuk bizonyítani. Fontos tulajdonság, hogy a fenti hasonlóság – matematikai nyelven – ekvivalencia reláció. Ebből következik, hogy a modell modellje a modellezettnek is modellje, ha azonos elvekkel készítettük, és így egy hosszú elvonatkoztatási folyamatnál is garantálni tudjuk, hogy a valóságról beszélünk. Másik elvárt tulajdonság, hogy a modellezett a saját modelljének modellje, a modell érvényességét igazolhatjuk, ha belátjuk, hogy a modellbeli események a valós rendszerben is bekövetkezhetnének.
Ezek után nézzük meg, hogy milyen tulajdonságokat várunk el modelljeinktől:
1. Elfogadhatóság
Egy modellt elfogadhatónak nevezünk, ha a létrehozásához megvizsgált eseményeket reprodukálni lehet vele. Ez alapvető követelmény, ha ez sem teljesül, akkor a modellben komoly hiba van.
2. Alkalmazhatóság
Egy modellt alkalmazhatónak nevezünk, ha használatából következtethetünk olyan, a valós rendszerben lezajló eseményekre, amelyeket korábbi megfigyeléseinkkel nem tapasztaltunk (de természetesen ott is bekövetkezhetnének, mivel magyarázhatók a valós rendszer keretei között).
3. Használhatóság
Egy modellt – jól – használhatónak nevezünk, ha a szimuláció paramétereit a természetes jelenség mérhető jellemzőiből kevés és egyszerű transzformáció segítségével kaphatjuk, illetve eredményeiből közvetlenül – vagy szintén elemi átalakítások útján – következtethetünk a jelenség valós jellemzőire.
4. Teljesség
A modell – mivel a valós rendszerből bizonyos körülmények, környezeti hatások elhagyásával keletkezett – csak a „lehetséges világ” egy megadott tartományában használható. Teljességnek nevezzük ezen tartomány valamilyen mértékét (bár nem állítjuk, hogy ez mindig számszerűsíthető). A teljesség megfogalmazható egyszerű esetben a figyelembe vehető paraméterek számával és értelmezési tartományával.
A programozás jelen esetben az ún. számítógépes modell létrehozását jelenti. Míg a modelltől azt vártuk, hogy objektumai és azok kapcsolatai megfeleljenek a valós rendszernek, addig a számítógépes modellel szemben egészen más elvárásaink is vannak.
Az első probléma, amit figyelembe kell venni: a számítógép memória-kapacitásának véges volta. Ez nagyobb szimulációs programoknál komoly nehézséget okozhat. A programírást úgy kell végezni, hogy amíg a hely nem okoz problémát, addig a lehető legegyszerűbb kódolási stratégiát válasszuk (ezzel elérjük, hogy szimulációs programjaink gyorsan elkészüljenek és könnyen felismerhető legyen bennük a modell struktúrája), amikor pedig a számítógép kicsinek bizonyul, akkor foglalkozzunk csak memóriatakarékos módszerekkel! Mit lehet ilyen esetekben tenni? A helyfoglalás csökkentését két úton érhetjük el, két dologra kell figyelnünk:
Az első esetben a programon memóriaigényt csökkentő transzformációkat kell végezni! Ehhez ismerni kell egyrészt az adott programozási nyelv jellemzőit, másrészt pedig a program struktúráját. Lehetőségeink:
A globális hatékonyság eléréséhez a modellen kell transzformációkat végeznünk, pontosabban a modell objektumain. Modelljeinkben általában egyedi objektumokat vizsgálunk, hiszen az adott jelenségből ezeket ismerjük, s így a modellkészítés ezek alapján a legkönnyebb. Sokszor előfordul azonban, hogy ezen objektumok közül bármelyik kettő nem különböztethető meg egymástól, azonos tulajdonságú objektumok osztályaiba sorolhatók. Ebben az esetben a tudásunk az osztályok reprezentáns elemeire vonatkozik. Ekkor az objektumok helyett foglalkozzunk az objektumosztályokkal; az objektumok közötti kapcsolatokat, a rajtuk végzett műveleteket helyettesítsük az osztályok közötti kapcsolatokkal, műveletekkel; így modellünk globális helyfoglalását lényegesen csökkenthetjük.
A második, problémát okozó tényező, a számítógép sebessége. A szimulációs programnak véges, kivárható időn belül eredményt kell produkálnia, így amikor egy szimulációs program lassúnak bizonyul, akkor meg kell vizsgálnunk gyorsításának lehetőségeit! Hatékonyságról is két szempont szerint beszélhetünk:
A lokális hatékonyság eléréséhez újra a programozási nyelv és a programszerkezet ismerete szükséges, például a következőket tehetjük:
A globális hatékonyság növeléséhez a modellt kell átalakítanunk. A legtöbb esetben egyedi események szimulációjával foglalkozunk, pedig az események – úgy, mint az objektumok – általában osztályokba sorolhatók. A megoldás így az eseményosztályok szimulációja lehet.
A harmadik tényező a számítógép pontossága lehet. Ez különösen analitikus megfogalmazású modelleknél okozhat gondot. Amennyiben szimulációs programoknál ilyen előfordul, úgy vagy nagy pontosságú aritmetikai műveletekre van szükségünk, vagy pedig korrekciós műveleteket kell bevezetnünk. Például ha valahány kiszámítandó érték összegét pontosan ismerjük, akkor lehetőségünk van a várt és a tényleges összeg különbségét szétosztani a tagok között; vagy pedig az utolsó tagot a megadott módszer helyett a várt összeg és az előző tagok összegének különbségével számolni.
A számítógépes modell megalkotása, a számítógépes szimuláció alkalmazhatósága lehetővé teszi egy „új, tapasztalati matematika” kialakítását. A feladatok megoldásának egy új módját teszi lehetővé, mely a jelenségek közvetlen utánzására és nagypontosságú megfigyelések elvégzésére épít, lehetővé teszi elemi események nagyon sokszori végrehajtását.
Amennyiben rendelkezésünkre áll a számítógépes program, elkezdhetjük a vele való kísérletezést, nem mindegy azonban, hogy ezt hogyan végezzük.
A kísérletezést meg kell tervezni! (A programot itt más módszerekkel próbáljuk ki, mint azt a tesztelésnél tettük.)
A legegyszerűbb esetben a szimuláció eredménye(i) egy paramétertől függ(enek). Ekkor, ha pl. lineáris kapcsolatot keresnénk az eredmény és a paraméter között, akkor (matematikai ismereteink szerint) elég lenne két kísérletet végezni, mivel két pont mindig egyértelműen meghatároz egy egyenest. Ez az állítás azonban hibás, a valós rendszert soha nem tudjuk pontosan megfigyelni, megfigyelt adatainkban mindig van hiba (ez időnként jelentős lehet). Ezért annyi kísérletet kell elvégezni, amely már statisztikai módszerekkel értékelhető. Ha ismerjük a paraméterek kritikus értékeit (amelyek körül a rendszer viselkedésében jelentős változás áll be), akkor ezek körüli értékekkel is el kell végezni a szimulációt (sőt nagyobb „gondossággal”, finomabb felosztással).
Ha több paraméteres modellt készítettünk, akkor bonyolultabb a helyzet. Követendő módszer lehet az, hogy az egyik paraméter értékét rögzítve, a másik paraméter hatását vizsgáljuk (két paraméter esetén). Ezután az első paramétert más értéken rögzítve újra végrehajtjuk a fenti tevékenységet. Ha így elég információt szereztünk, akkor megpróbálhatjuk a két paraméter szerepét felcserélni. Kettőnél több paraméter esetén ez az eljárás már bonyolult lehet, nem is szólva arról, hogy nagyon kevés információt adhat (általános esetben) az egész rendszer viselkedéséről. Lehet még próbálkozni olyan módszerrel, hogy két paramétert változtatunk úgy, hogy az egyik a másiknak valamilyen függvénye legyen, így egy kicsit általánosabb képet nyerhetünk a rendszerről, de a bonyolultság lényegesen növekszik.
Más módszert is lehet találni kísérletek tervezésére, ha tudunk valamit a paraméterek és eredmények várható kapcsolatáról. Legegyszerűbb ilyenkor az az eset, amikor nem a konkrét függvényre van szükségünk, hanem csak a jellegére („ha ezt a paramétert növelem, akkor az eredmény is növekedni fog” típusú állításokat akarunk belátni). Ilyenkor olyan kísérleti tervet kell elkészíteni, amely teljes (tartalmazza a paraméterértékek összes jellemző kombinációját), ugyanakkor pedig nem tartalmaz felesleges kísérleteket (olyanokat, amelyeknek eredményére már következtetni lehet a többi kísérlet eredményéből). Az első követelmény annak érdekében fontos, hogy a valóságról minél pontosabb képet kapjunk; a második pedig a szimuláció hatékonyságával kapcsolatos (gyakran előfordul, hogy 20-30 kísérletet is elvégzünk olyankor, amikor elég lett volna esetleg 4-5 is).
Különböző módszerekkel a kezdetben bevezetett változóink helyett független faktorokat vezettünk be. A faktorok általában egy bizonyos tartományon belül különböző értékeket vehetnek fel; a folytonos értékkészletű faktorokról is gyakran feltételezzük ezt. A legegyszerűbb esetben minden faktor pontosan két értéket vehet fel, s egy kísérletet ezek egy lehetséges kombinációja határoz meg. Ha a rendszert matematikailag egy lineáris függvény írja le, akkor elsőrendű, ha egy másodfokú polinom, akkor másodrendű kísérleti tervet készítünk.
Magasabb rendű feladatokkal nem foglalkozunk, gyakran használható azonban két egyszerű transzformáció:
Ha a keresett kapcsolat y=f(g(x)) alakú (ahol g lineáris függvény), akkor a z=f-1(y)=g(x) összefüggés vizsgálatával foglalkozunk, ha pedig y=g(h(x)) alakú (ahol g lineáris függvény), akkor az y=g(w) és a w=h(x) összefüggéseket vizsgáljuk.
Az eddigiekben ún. előredeterminált kísérletsorozatokat javasoltunk, van azonban más lehetőség is. Egy adaptív kísérletsorozatban az egyes kísérletek, vagy a kísérletsorozat részsorozatai választásánál felhasználjuk az előző kísérletek eredményeit (itt nem érvényes a megfigyelésekhez megállapított szabály). Ez a módszer akkor is hasznos, amikor ún. érkezési kísérleteket hajtunk végre, azaz egy adott célhoz (eredmény) keresünk bemenő paramétereket (ilyenkor nem érdekes maga az összefüggés sem).
Az összevetés célja annak megállapítása, hogy a modellünk (modell, program, szimulált adatok) megfelel-e a megfigyelt adatoknak. Ez biztosítja ugyanis, hogy jogunk van a szimulált adatokból következtetni a valós rendszer működésére. (Természetesen, ha már a megfigyeléseink is hibásak voltak, akkor ez nem áll fenn, de azok helyességét így nem ellenőrizhetjük.) Itt egy látszólagos ellentmondás található: ha a szimulált eredményeknek azonosaknak kell lenniük a (már ismert!) megfigyelt eredményekkel, akkor miért van szükség erre a bonyolult folyamatra, mi újat tud ez adni? Az ellentmondás valóban látszólagos, a megoldás a kezdeti problémánkból adódik, ahol megfogalmaztuk, hogy a valódi kísérleteket miért kell számítógéppel pótolni. Módszerünk az, hogy a kísérletet elvégezzük néhányszor a valós rendszerben, azzal a céllal, hogy a modellt létre tudjuk hozni, illetve helyességét be tudjuk látni; majd a valós rendszerrel kapcsolatos kérdéseinkre a számítógépes modellel kapcsolatos kísérletekből keresünk választ.
Hogyan tudjuk eldönteni, hogy a modellünk megfelel-e a valóságnak? Ez nagyon nehéz probléma, nézzünk meg néhány lehetséges módszert (fogjuk fel a valós rendszer és a szimulált rendszer működését egy-egy – általában sztochasztikus – folyamatnak):
Hasznos lehet a modellel olyan szélsőséges esetekben is kísérleteket végezni, amelyek a valóságban nem, vagy nagyon kicsi valószínűséggel fordulnak elő, ebben az esetben a kapott eredményeknek a valós rendszer keretei között is magyarázható eredményt kell adniuk.
Ha az összevetésből azt az eredményt kapjuk, hogy a modell nem felel meg a valóságnak, annak három oka lehet:
Gyakran vezet hibás értelmezésre két tényező, ha nem vesszük figyelembe:
Az első tényezőből fakadó hibák kiküszöbölésére néha jó lehet az a módszer, ha „elég hosszú” futási időt vizsgálunk, de ez nem megoldás abban az esetben, ha a kezdőállapot-választásnak lényeges szerepe van a rendszerben (pl. az ún. nem visszatérő folyamatok esetében), illetve nagyon nehéz megmondani, hogy mennyi az az „elég hosszú” idő.
A második tényezőből fakadó hibák kiküszöbölésére jó módszer sok kísérlet elvégzése azonos körülmények között, és a kapott eredmények átlagának felhasználása (kivéve, ha az így kapott hiba szisztematikusan mindig egy irányban hamisítja az eredményeinket).
Hasonlítsuk össze a kapott eredményeket:
Az első esetben mindkétszer a fokozatos kiegyenlítődést kaptuk eredményül. A másodikban az átlagos érték azonos maradt, ... azaz a modell megfelel elvárásainknak.
Mielőtt rátérnénk a konkrét módszerekre, nézzük meg, hogy általában miért végzünk el egy kísérletet (kísérletsorozatot), miért végzünk megfigyeléseket (megfigyelés sorozatokat), mi az, amit tudni akarunk a jelenségről. Ehhez kapcsolódóan nézzük meg azt is, mi az, amit eredményként adhatunk, kiszámolhatunk.
Gyakoriak az olyan kísérletek, amelyek egy-egy termék, termény bizonyos paramétereinek javítását tűzik ki célul. Legyen az a feladata egy kutatóintézetnek, hogy minél magasabb fehérjetartalmú búzát nemesítsen! Kíváncsiak arra, hogy az így nyert búzaszemeknek mekkora a várható fehérjetartalma, mennyire egyformák (fehérjetartalom szempontjából).
Ezért a learatott búzából mintát vesznek, meghatározzák a búzaszemek fehérjetartalmát, majd ezek alapján megbecsülik ennek várható értékét. Ez azonban kevés lehet annak eldöntéséhez, hogy mennyire „megbízhatóan” jó az adott búza. Szükség van a várható érték körüli szórásra is. A kettő együtt használhatóbb eredményt ad a további munka megtervezéséhez.
Az előbbi példánál maradva még több információ áll rendelkezésünkre, ha meg tudjuk adni azt az intervallumot, amibe nagy valószínűséggel beleesik a várható érték. Minél kisebb az intervallum hossza – megfelelő rögzített valószínűség mellett – annál jobban bízhatunk a búzaszemek egyformaságában, azonos minőségében. Az így meghatározott intervallumot konfidencia intervallumnak nevezzük.
Tegyük fel, hogy az ország két különböző helyén, az így nemesített vetőmagot azonos időben elvetették, majd azonos időben learatták. Kíváncsiak vagyunk arra, hogy a két termésbeli fehérjetartalmak mennyire egyformák, mennyire függnek egymástól. Minél szorosabb a kapcsolat köztük, annál jobban bízhatunk a búza stabil minőségében, annál kevésbé fontosak más tényezők (pl. talajminőség, időjárás stb.).
Fontos lehet a búzaszemek fehérjetartalmának eloszlása is. Ehhez a lehetséges értékeket megfelelő számú – nem túl sok – intervallumra osztjuk, majd meghatározzuk az egyes intervallumba eső búzaszemek számát. Ezzel egy diszkrét eloszlást definiálunk, amit az egyes intervallumok feletti téglalapokkal ábrázolva – ezt nevezzük hisztogramnak – egy diszkrét eloszlásfüggvényt kapunk.
Vizsgálhatjuk azt is, hogy mennyire függ a talaj minőségétől a terméseredmény. Ilyenkor a talaj minőségének függvényeként kívánjuk megbecsülni a búza fehérjetartalmát. Ezért az azonos minőségű vetőmagot, több különböző minőségű talajba vetik. Betakarítás után a fehérjetartalmakat megmérve, összefüggést keresnek a talajminőség, mint független változó, és a fehérjetartalom, mint függő változó között. A kapott függvény görbéjét nevezzük regressziós görbének.
Adott egy N elemű minta. A mért jellemző értékei egy Jel tömbben vannak! Határozzuk meg a jellemző tapasztalati várható értékét, szórásnégyzetét! A későbbiek során szükségünk lesz a korrigált szórásnégyzetre is, ezért azt is számoljuk ki! A következő képletek alapján számolunk:
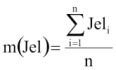
Várható_érték(N,Jel):
v:=0
Ciklus i=1-től N-ig
v:=v+Jel(i)
Ciklus vége
Várható_érték:=v/N
Függvény vége.
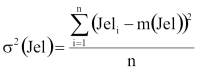
Szórásnégyzet(N,Jel):
szn:=0; v:=Várható_érték(N,Jel)
Ciklus i=1-től N-ig
s:=Jel(i)-v; szn:=szn+S*S
Ciklus vége
Szórásnégyzet:=szn/N
Függvény vége.
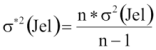
Korrigált_szórásnégyzet(N,Jel):
Korrigált_szórásnégyzet:=N*Szórásnégyzet(N,Jel)/(N-1)
Függvény vége.
Adott egy N (N≥5) elemű minta. Azt feltételezzük – joggal –, hogy az N elemű minta valamilyen (m, σ) normális eloszlású. A mért jellemző értékei egy Jel tömbben vannak! Határozzuk meg P (90≤P≤99.9) százalékos megbízhatósággal az elméleti várható értéket tartalmazó intervallumot! Az intervallum végpontjai a VK, illetve a VV változókban lesznek! Ennek meghatározásához szükségünk lesz egy táblázatra, amely különböző megbízhatósági szintekhez és különböző mintaelem-számokhoz tartozó konstansokat tartalmaz, melyek az intervallum meghatározásához kellenek. Természetesen nem az összes lehetségeset adjuk meg, csak az általunk legfontosabbaknak tartottakat. Ha az adatok nem a táblázat értékeinek megfelelőek, lineáris közelítéssel határozzuk meg a megfelelő konstans értékét.
P \ N | 5 | 20 | 40 | 60 | 120 | >120 |
|---|---|---|---|---|---|---|
90% | 2.132 | 1.729 | 1.684 | 1.671 | 1.658 | 1.645 |
95% | 2.776 | 2.093 | 2.021 | 2.000 | 1.980 | 1.960 |
99% | 4.604 | 2.861 | 2.774 | 2.660 | 2.617 | 2.576 |
99.9% | 6.859 | 3.850 | 3.551 | 3.460 | 3.373 | 3.291 |
Az intervallum kezdő-, illetve végpontja a következő formulákból adódik:
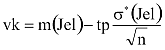
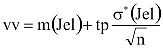
ahol tp a p megbízhatósági szinttől és az N mintaelem-számtól függő konstans.
Az ST(4,6) tömb 0. sorában a mintaelem-számok, a nulladik oszlopában a megbízhatósági szintek lesznek.
Konfidencia intervallum meghatározása(N,Jel,P,VK,VV):
Az ST tömb feltöltése; VK:=0; VV:=0
Konstans meghatározása(P,ST,L0,L1)
[L0 : Van-e a táblázatban N elemű minta,
L1 : Van-e a táblázatban P megbízhatósági szint]
Elágazás
L0 és L1 esetén TP:=ST(I,J)
L0 és nem L1 esetén TP:=M_szint_köz(I,J,ST(,))
nem L0 és L1 esetén TP:=M_elem_köz(I,J,ST(,))
nem L0 és nem L1 esetén TP:=Kereszt_köz(I,J,ST(,))
Elágazás vége
VE:=Várható_érték(N,Jel)
SZNK:=Korrigált_szórásnégyzet(N,Jel)
VK:=TP*SQR(SZNK/N); VV:=VE+VK: VK:=VE-VK
Eljárás vége.
Konstans meghatározása(P,ST(,),L0,L1):
P0:=(100-P)/100; j:=0
Ciklus
j:=j+1; L0:=(ST(0,j)>N)
amíg L0
Ciklus vége
i:=0
Ciklus
i:=i+1; L1:=(abs(ST(i,0)-P0)>0.0001)
amíg L1
Ciklus vége
Eljárás vége.
M_szint_köz(i,j,ST(,)):
TP:=(ST(i,j)-ST(i-1,j))/(ST(i,0)-ST(i-1,0))
M_szint_köz:=TP*(P-ST(i-1,0))+ST(i-1,j)
Függvény vége.
M_elem_köz(i,j,ST(,)):
TP:=(ST(i,j)-ST(i,j-1))/(ST(0,j)-ST(0,j-1))
M_elem_köz:=(TP*(N-ST(0,j-1))+ST(i,j-1)
Függvény vége.
Kereszt_köz(i,j,ST(,)):
TP0:=M_szint_köz(i,j-1); TP1:=M_szint_köz(i,j)
TP:=(TP1-TP0)/(ST(0,j)-ST(0,j-1))
Kereszt_köz:=TP*(N-ST(0,j-1))+TP0
Függvény vége.
Adott két N elemű minta. A mért jellemzők az X, illetve az Y tömbökben vannak. Határozzuk meg a köztük levő függőségi viszony mértékét! Egy számértéket fogunk meghatározni, amelynek abszolút értéke 1-nél nem nagyobb. Minél jobban függnek egymástól, abszolút értékben, annál közelebb kerülünk az 1-hez. Ha a két változó között a kapcsolat lineáris, azaz y=a+bx, akkor b>0 esetén e számérték 1, ha b<0, akkor pedig -1. Ha függetlenek egymástól, akkor ez az érték 0 lesz. Fordítva ez nem igaz: ha 0 korrelációjúak, azaz korrelálatlanok, abból nem következik a függetlenségük! Eredményül az K-ban kapjuk a korrelációs együttható értékét.
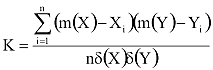
Korrelációs_együttható(N,X,Y):
vX:=Várható_érték(N,X); vY:=Várható_érték(N,Y)
s:=0
Ciklus i=1-től N-ig
s:=s+(X(i)-vX)*(Y(i)-vY)
Ciklus vége
sznX:=Szórásnégyzet(N,X); sznY:=Szórásnégyzet(N,Y)
Korrelációs_együttható:=s/gyök(sznX*sznY)/N
Függvény vége.
 |
 |
 |
| Készült az "Országos koordinációval a pedagógusképzés megújításáért” című TÁMOP-4.1.2.B.2-13/1-2013-0007 pályázat keretében. (ISBN 978-963-284-631-6) | ||
A tananyag az ELTESCORM keretrendszerrel készült