Modellezés és szimuláció

4. Keretmodellek

Ebben a fejezetben általános keretet szeretnénk adni konkrét fizikai, kémiai, biológiai modellek vizsgálatához. Olyan általános modelleket vizsgálunk, melyek segítségével a fenti területeken könnyebb lesz új modelleket készíteni.

Elöljáróban hangsúlyoznunk kell, hogy feltesszük: a valóság jelenségei megismerhető részjelenségekre bonthatók, s ezek a részjelenségek egyetlen időpontban megadott jellemzők (állapot, paraméter) segítségével csatolhatók a valóság többi részéhez, és a fenti peremfeltételek akárhányszor újra megvalósíthatók („csodákkal nem foglalkozunk”).

A modelleket két nagy osztályba soroljuk. Az egyikben a teljes jövőt előre kiszámítjuk (a kezdőállapotból), s azután csak a kiszámított jövő megjelenítése a feladat. A másikban az aktuális állapotból csak a következő időegységbeli állapotot határozzuk meg, majd abból számítjuk a következőt ...

Mi a szimulációs sorozatunkban elsősorban az utóbbi típusú modellekkel foglalkozunk.

A valós rendszerek, amelyeket modellezni szeretnénk, olyanok lesznek, hogy a rendszer elemei osztályokba sorolhatók, a rendszer állapotát ezen osztályok elemszáma fogja meghatározni, illetve egyes esetekben ezen osztályok térbeli eloszlása, mintázata.

Egyszerűbb esetekben csak egy osztályt vizsgálunk, s minden elemet ebbe sorolunk be, máskor minden osztályban csupán egy elem lesz. A legegyszerűbb pedig az az eset, amikor egy osztály létezik egy elemmel. Ekkor tulajdonképpen egy (néhány) képletet kell folyamatosan számolnunk, mint az alábbi példából is látható:

Példa

Egy 0 tömegű, D rugalmassági együtthatójú, „ideális” rugóra helyezett M tömegű test rezgésének szimulációja. Ismert az s₀ kezdeti kitérés, a nehézségi gyorsulás, a k közegellenállási együttható.

A szimuláció alapelve – kicsiny dT időintervallumokat választva, s azzal feltételezéssel élve, hogy dT idő alatt a paraméterek változásai elhanyagolhatóak, a fontos állapothatározók egyszerűen számíthatók, majd ezekből pl. állapotdiagram rajzolható:

Az F erő: F=Fr+Fk+G, Fr=D*s (rugóerő), Fk=k*v (közegellenállás), G=M*g

Az a gyorsulás: a=F/M

A v sebesség: v=a*dT

s kitérés: s=v*dT, s₀ kezdeti kitérés: s₀=M*g/D M*g=s₀*D

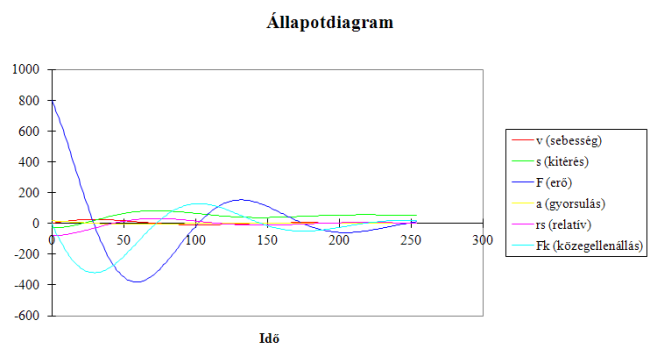Rugó állapotdiagram.

A rendszer egyes elemei véges sok állapotban lehetnek (diszkrét állapotú modell), s a rendszer elemszáma is mindig véges lesz. Minden egyes elem jövőbeni (következő időpillanat) állapotát csak a rendszer elemeinek adott időpillanatban meglevő állapota és a rendszer paraméterei határozzák meg (utóhatás mentesség – Markov tulajdonság). Most olyan feladatokkal fogunk foglalkozni, melyekben egy populációt vizsgálunk, s ezt mindig valamilyen egyedek összességének fogjuk fel (pl. atom, molekula, sejt, élőlény, társadalom stb.). Programjainkban ezért az egyes egyedekről kell valamilyen információt tárolnunk. Erre a célra táblázatokat használunk:

Ha az egyedek térbeli elhelyezkedésére nincs szükségünk, akkor egy vektort használunk, amelyben az egyes egyedek szimuláció szempontjából fontos jellemzői írjuk le.

Ha fontos az egyedek közötti szomszédság megállapítása – mozgás vagy kapcsolat szempontjából –, akkor két lehetőségünk van. Az egyszerűbb esetben a szimulációs teret ábrázoljuk, amelynek minden helyén vagy egy egyed szerepel, vagy pedig üres. A szimulációs tér ábrázolására kézenfekvő egy kétdimenziós táblázat (mátrix).

Ebben az esetben a fontos kérdés: kit tekintünk egy adott hely szomszédjának? A kérdésre kétféle válasz lehet: vagy a négyzetrácsbeli 4 oldalszomszédot választjuk szomszédnak, vagy pedig a 4 sarokszomszédot is.

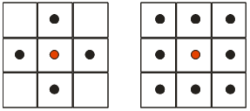Négyzetrácsos tér 4, illetve 8 szomszéddal.

Mindkét esetben geometriai problémák lépnek fel, ha megpróbálunk középső pontból eljutni valamelyik sarokszomszédba:

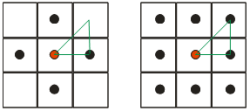A sarokszomszéd távolsága 4, illetve 8 szomszédos esetben.

A 4 szomszédos esetben a sarokszomszédba jutás 2 időegységbe kerül, azaz mintha az ábrán látható zöld derékszögű háromszög átfogó hosszúsága a két befogó hosszúságának összege lenne. A 8 szomszédos esetben a sarokszomszédba jutás 1 időegységet igényel, azaz olyan derékszögű háromszöget tételez fel, aminek mindhárom oldala azonos hosszúságú. Nyilvánvalóan mindkettő képtelenség.

Geometriából tudhatjuk, hogy a sík háromféle szabályos sokszöggel fedhető le, az általunk használt négyzetek mellett háromszögekkel és hatszögekkel is. A hatszöges lefedésben három szimmetriatengely fedezhető fel, nevezzük ezeket i-, j-, illetve k-tengelynek!

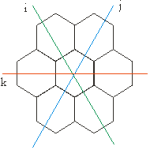Hatszögrács.

A i-tengely mentén i értéke állandó, tőle jobbra növekszik, balra pedig csökken. A j-tengely mentén j állandó, ettől balra növekszik, jobbra pedig csökken. A k-tengelytől felfelé csökken k értéke, lefelé pedig növekszik.

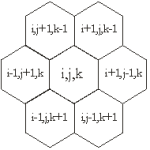Hatszögrács szomszédokkal.

Ilyen szabályszerűségek esetén a szomszédok kezelése algoritmizálható. Hatszögrács alakú programozási struktúrák azonban nincsenek.

Megfigyelhető azonban, hogy így a három index összege mindig ugyanaz – az (i,j,k) indexű hely bármely szomszédjánál az egyik index változatlan, a másik eggyel csökken, a harmadik eggyel nő – lehet például minden helyre i+j+k=0. Emiatt k értéke i-ből és j-ből mindig számítható, azaz ábrázolásban elég egy hagyományos mátrix, csupán a szomszédság meghatározásához kell a három index.

Könnyen belátható ugyanakkor, hogy a „hamis” geometriájú tér a jelenségek jellegét általában nem befolyásolja, csak a számított jellemzők pontos értékét. Ha erre nincs szükségünk, akkor maradhatunk a négyzetrácsos síklefedés mellett.

Elképzelhető ebben az esetben is az egyedek ábrázolása egy vektorban, ekkor azonban a vektornak tartalmaznia kell az egyes egyedek térbeli elhelyezkedését leíró adatokat – pl. a koordinátákat.

Ebben – és a következő – fejezetben az általánosabb esetet követjük, mindig NxM-es táblázatokat – eseménytér – használunk, melyben N és M értékét (azért, hogy statisztikailag értékelhető eredményt kapjunk) legalább 100-nak választjuk.

Két alapvető keretmodellt fogunk létrehozni, a következő elvek alapján:

• Az előforduló eseményeket folyamatosan figyeljük, egy időpillanatban 1 (esetleg több) esemény következhet be. A modell idejének nincsen szoros kapcsolata a valós rendszer idejével. (Folytonos keretmodell)
• Az előforduló eseményeket diszkrét időközönként figyeljük. Egy időpontban a rendszer minden elemével „történik valami”. A diszkrét időközök megfelelnek a valós rendszer idejének valamilyen rögzíthető időtartamainak. (Diszkrét vagy generációs keretmodell)

A két keretmodell közös része:

Itt egy általános feladat megoldási elvet használtunk, amely egy feladat többszöri megoldására szólít fel.

Mindkét keretmodell esetén még egy felbontást készítünk, valamilyen változást szeretnénk nyomon követni, amely lehet:

• állapotváltozás,
• hely- (helyzet-) változás.

Az utóbbit az állapotváltozás speciális esetének foghatjuk fel, csupán a későbbi hivatkozások érdekében vizsgáljuk különállóan.

Adott egy NxM-es táblázat, amelyen eseményeket figyelhetünk meg. A táblázat egy eleme egy egyedet (atom, molekula, sejt, élőlény, társadalom stb.) jelent, amelynek két fajtáját (populációt) fogjuk ábrázolni. A táblázatot valamilyen kezdeti – megadott – eloszlás alapján – általában véletlenszerűen – kitöltjük. Ezután kezdődhetnek a változások, az „események”, amit „A feladat konkrét megoldása” eljárás fog elvégezni.

4.1. Folytonos keretmodell

A változtatást úgy valósítjuk meg, hogy kiválasztjuk – valamilyen szabály – szerint a táblázat egy (vagy több) elemét, majd az ott levő egyed felhasználásával módosítjuk a táblázatot.

Olyan ciklust, mint amelyet ebben a programban használtunk, akkor írunk, amikor a ciklus befejeződésének előidézését a program majdani használójára akarjuk bízni, mivel azt, hogy a szimulációt mennyi ideig érdemes követni, a használó szubjektív véleménye alapján döntheti el.

Folytonos diffúziós modell

A módosítás folyamata itt másképpen történik: kiválasztunk egy elemet a táblázatból, majd megcseréljük környezetének egy véletlenszerűen kiválasztott elemével. A változás itt mozgást jelent!

Vissza a tartalomjegyzékhez

4.2. Diszkrét (generációs) keretmodell

Egy új táblázatot kell készíteni úgy, hogy az első táblázat valamennyi elemét módosítjuk valamilyen szabály szerint és a továbbiakban csak az új táblázattal (új generáció) foglalkozunk.

Diszkrét diffúziós modell

A módosítás folyamata itt úgy történik, hogy a táblázat összes elemével végzünk valamilyen mozgást.

Vissza a tartalomjegyzékhez

4.3. Sejtautomata-elvű keretmodell

A mozgást szemléltető modellek alapvető problémája a szimulációs program sebessége lesz. A megfigyelt térrész növelésekor a megoldást kivárhatatlanul hosszú idő alatt kapjuk csak meg. Ez a probléma sokkal élesebben vetődik fel akkor, amikor a mozgás, az „áramlás” bonyolultabb szabályok szerint megy végbe. Erre a problémára adnak választ a sejtautomata-elvű modellek.

Osszuk fel a vizsgált térrészt azonos méretű cellákra (sejtekre)! Minden egyes sejtre meg fogjuk adni az állapotát (pl. adott időpillanatban mennyi molekulát, energiát, egyéb elemi objektumot tartalmaz). A diszkrét keretmodellre építhetjük a sejtautomata típusú modelleket, az összes sejt párhuzamos (azonos időbeli) állapotváltozását fogjuk megadni. Minden egyes sejt következő időpillanatbeli állapota függ egyrészt a saját állapotától, másrészt pedig szomszédai, valamilyen környezete állapotától (de a távolhatást nem engedjük meg). Ezt az állapotváltozást írja le az ún. állapotátmenet-függvény.

A szomszédság kérdése: a választott időegységtől függően többnyire 4 vagy 8 szomszédot veszünk figyelembe. v*Δt << a esetén a 4 a jó közelítés, ahol v: az áramlás sebessége, Δt: az időegység, a: a sejt-„kocka” oldalhossza.

Meggondolandó: hogyan kapjuk a diffúzió véletlenszerű mozgásából az állapotátmenet függvényt? Erre a kérdésre a választ úgy kaphatjuk meg, ha – feltételezve, hogy minden cellán belül egyenletes az eloszlás (a sebességeloszlás is) – meghatározzuk, hogy a cellában levő molekulák hány százaléka képes egy időegység alatt elhagyni a cellát (ez a diffúziós sebesség).

Tartalmazza a sejttér régi állapotát az R(N,M) mátrix, az újat pedig az U(N,M). A modellben nemnegatív (valós) számok fogják azonosítani az egyes sejtek állapotait, illetve -1 fogja jelölni azokat a sejteket, amelyek mintegy falat határoznak meg a sejttérben, azaz nem változhatnak, s rajtuk keresztül a mozgás sem történhet. Célszerű lesz kezdetben az a feltételezés, hogy sejtterünk szélein ilyen fal típusú sejtek találhatóak.

Ez a modell homogén és izotróp teret feltételez (a diffúzió sebessége helytől és iránytól független). Az általános algoritmusban a szimulációs lépés a következő elemi lépésekből áll:

A változás azt jelenti, hogy a sejttér adott pontjára a környezetből anyag (energia) áramlik. Megadhatjuk az állapotátmenet függvényt, vagy pedig azt az algoritmust, amellyel ezt az átmenetet megvalósítjuk. Ez utóbbi:

Minden egyes sejtből a teljes anyagmennyiség D-szerese fog kiáramlani 4 szomszédja közül mindegyikbe (D<<1/4):

Vissza a tartalomjegyzékhez