Szükséges előismeret: Függvények aszimptotikus viselkedése, Jelölések
B+ fa (B+ tree)
B+ fa:
Ábrázolásai:
Invariánsok:
- Minden levélben legfeljebb $d-1$ kulcs, és ugyanennyi adatrekordra hivatkozó mutató található.
- A gyökértől mindegyik levél ugyanolyan távol található, vagyis minden levél azonos mélységben, a legalsó szinten van. (tökéletesen kiegyensúlyozott keresőfa)
- Minden belső csúcsban eggyel több mutató van, mint kulcs, ahol $d$ a felső határ a mutatók számára.
- Minden $N$ belső csúcsra (ahol $k$ az $N$ csúcsban a kulcsok száma):
- az első gyerekhez tartozó részfában minden kulcs kisebb, mint az $N$ első kulcsa
- az $i$-edik gyerekhez tartozó részfában $(2 \le i \le k)$ lévő tetszőleges $r$ kulcsra $\text{N.kulcs}[i-1] \le r \lt \text{N.kulcs}[i]$.
- az utolsó gyerekhez tartozó részfában minden kulcs nagyobb-egyenlő, mint az $N$ utolsó kulcsa
- A gyökércsúcsnak legalább két gyereke van, kivéve, ha ez a fa egyetlen csúcsa.
- Minden, a gyökértől különböző belső csúcsnak legalább $\lfloor d / 2 \rfloor$ gyereke van.
- Minden levél legalább $\lfloor d / 2 \rfloor$ kulcsot tartalmaz, kivéve, ha a fának egyetlen csúcsa van.
- A B+ fa által reprezentált adathalmaz minden kulcsa megjelenik valamelyik levélben, balról jobbra szigorúan monoton növekvő sorrendben.
Fokszáma:
- a kulcs méretétől,
- a mutató méretétől,
- a blokk méretétől.
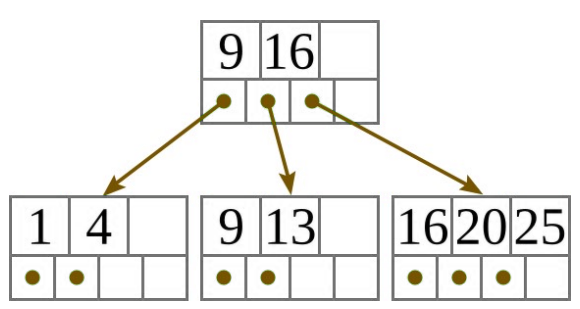
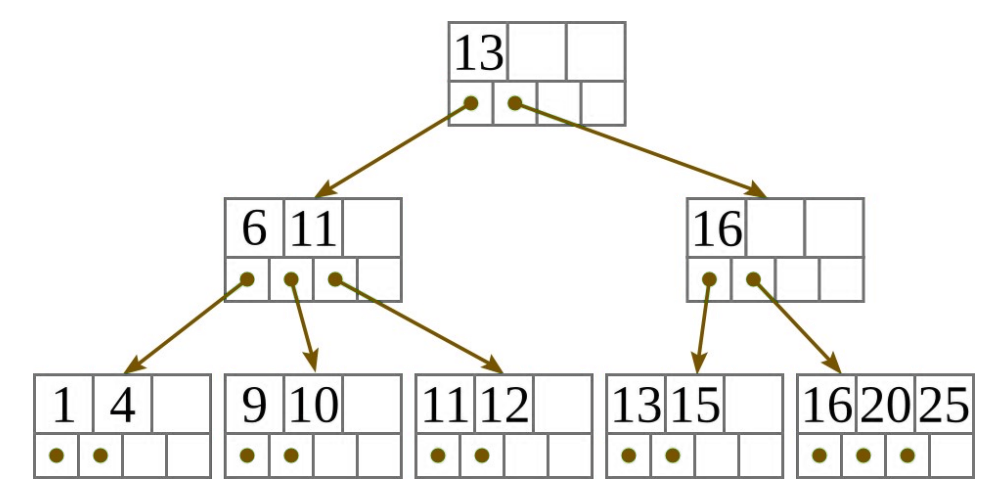
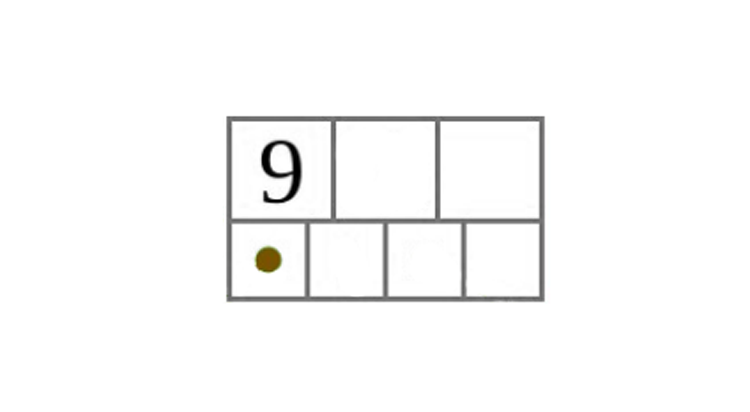
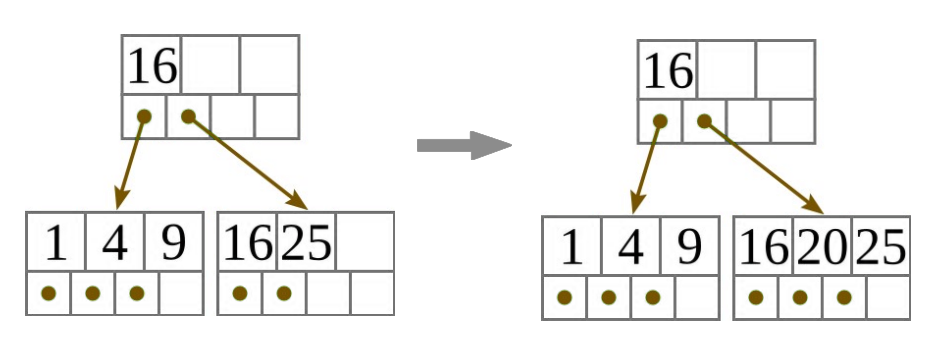
Példa:
A műveletigényről
Beszúrás:
- Ha a levélben márszerepel a kulcs, a beszúrás sikertelen.
- Különben szúrjuk be a kulcs/mutató párt a levélbe.
Beszúrás a levélbe:
- Ha a csúcsban van üres hely, szúrjuk be a megfelelő kulcs/mutató párt kulcs szerint rendezetten ebbe a csúcsba!
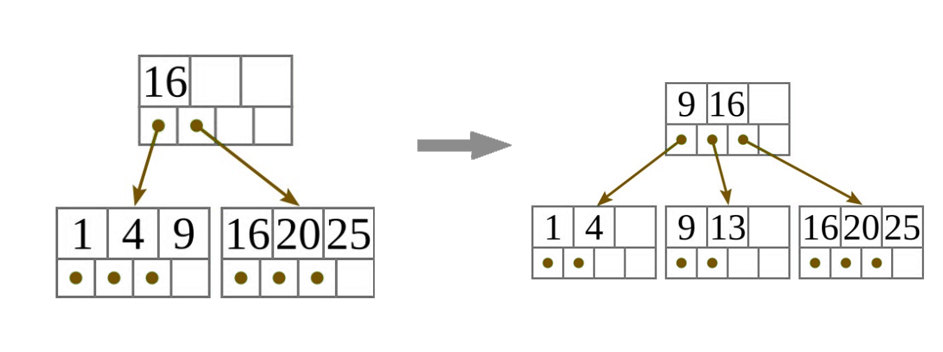
- Ha a csúcs már tele van, vágjuk szét két csúccsá, és osszuk el a $d$ darab kulcsot egyenlően a két csúcs között!
Szétvágás:
- Ha a csúcs egy levél, vegyük a második csúcs legkisebb értékének másolatát, és ismételjük meg ezt a beszúró algoritmust, hogy beszúrjuk azt a szülő csúcsba!
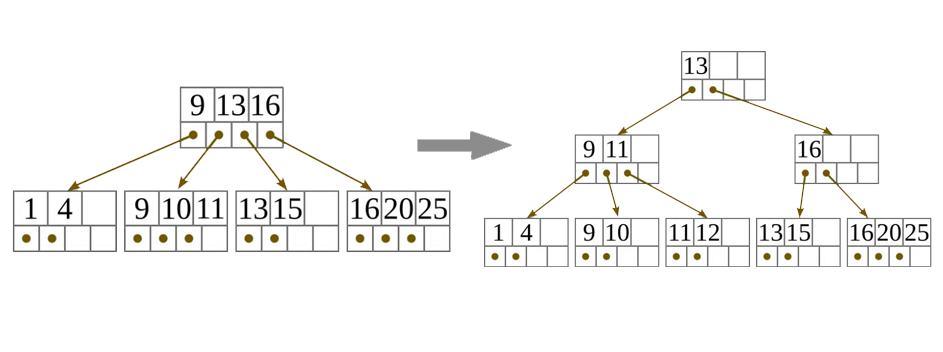
- Ha a csúcs nem levél, vegyük ki a középső értéket a kulcsok elosztása során, és ismételjük meg ezt a beszúró algoritmust, hogy beszúrjuk ezt a középső értéket a szülő csúcsba!
Törlés:
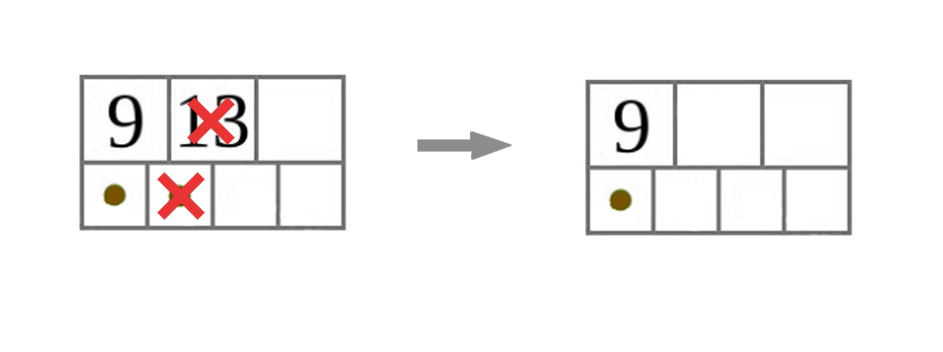
- A keresés során megtalált levélcsúcs egyben a gyökércsúcs is.
- Töröljük a megfelelő kulcsot és a hozzá tartozó mutatót a csúcsból!
- Ha a csúcs tartalmaz még kulcsot, kész vagyunk.
- Különben töröljük a fa egyetlen csúcsát, és üres fát kapunk.
- A keresés során megtalált levélcsúcs nem a gyökércsúcs. Ekkor törlünk a levélcsúcsból.
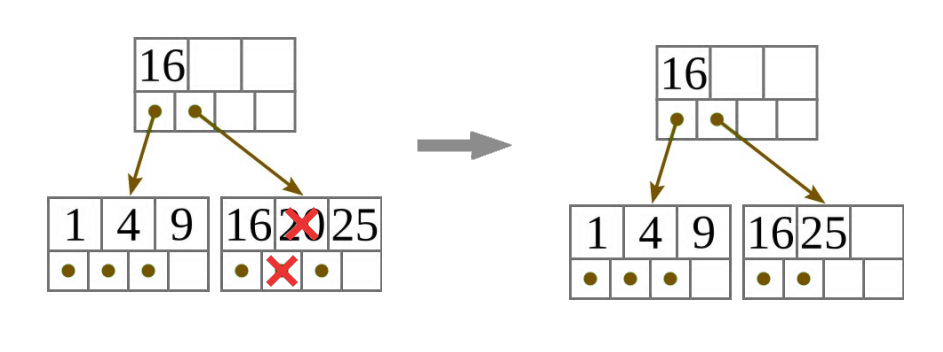
Törlés levélcsúcsból:
- Töröljük a megfelelő kulcsot és a hozzá tartozó mutatót a levélcsúcsból!
- Ha a levélcsúcs még tartalmaz elég kulcsot és mutatót, hogy teljesítse az invariánsokat, kész vagyunk.
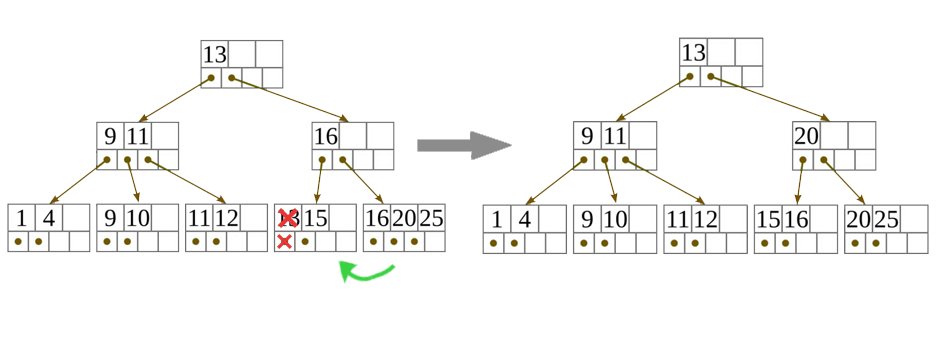
- Ha a levélcsúcsban már túl kevés kulcs van ahhoz, hogy teljesítse az invariánsokat, de a következő, vagy a megelőző testvérének több van, mint amennyi szükséges, osszuk el a kulcsokat egyenlően közte és a megfelelő testvére között! Írjuk át a két testvér közös szülőjében a két testvérhez tartozóhasító kulcsot a két testvér közül a második minimumára!
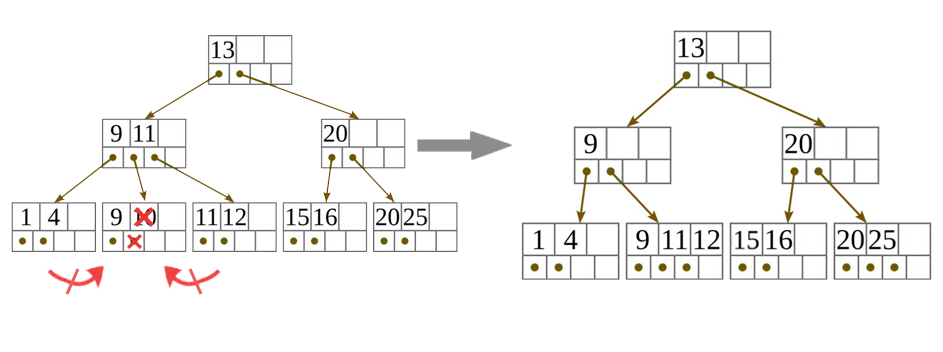
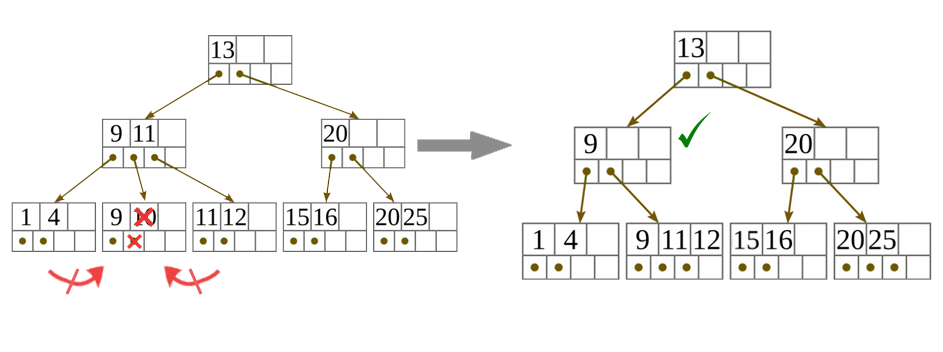
- Ha a levélcsúcsban már túl kevés kulcs van ahhoz, hogy teljesítse az invariánst, és a következő, valamint a megelőző testvére is a minimumon van, hogy teljesítse az invariánst, akkor egyesítsük egy vele szomszédos testvérével! Ennek során a két testvér közül a (balról jobbra sorrend szerinti) másodikból a kulcsokat és a hozzájuk tartozó mutatókat sorban átmásoljuk az elsőbe, annak eredeti kulcsai és mutatói után, majd a második testvért töröljük. Ezután meg kell ismételnünk a törlő algoritmust a szülőre, hogy eltávolítsuk a szülőből a hasító kulcsot (ami eddig elválasztotta a most egyesített levélcsúcsokat), a most törölt második testvérre hivatkozó mutatóval együtt.
Törlés belső - gyökértől különböző - csúcsból:
- Töröljük a belső csúcs éppen most egyesített két gyereke közti hasító kulcsot és az egyesítés során törölt gyerekére hivatkozó mutatót a belső csúcsból!
- Ha a belső csúcsnak van még $\lfloor \frac{d}{2}\rfloor$ gyereke, (hogy teljesítse az invariánsokat) kész vagyunk.
- Ha a belső csúcsnak már túl kevés gyereke van ahhoz, hogy teljesítse az invariánsokat, de a következő, vagy a megelőző testvérének több van, mint amennyi szükséges, osszuk el a gyerekeket és a köztük levő hasító kulcsokat egyenlően közte és a megfelelő testvére között, a hasító kulcsok közé a testvérek közti (a közös szülőjükben lévő) hasító kulcsot is beleértve! A gyerekek és a hasító kulcsok újraelosztása során, a középső hasító kulcs a testvérek közös szülőjében a két testvérhez tartozó régi hasító kulcs helyére kerül úgy, hogy megfelelően reprezentálja a köztük megváltozott vágási pontot! (Ha a két testvérben a gyerekek összlétszáma páratlan, akkor az újraelosztás után is annak a testvérnek legyen több gyereke, akinek előtte is több volt!)
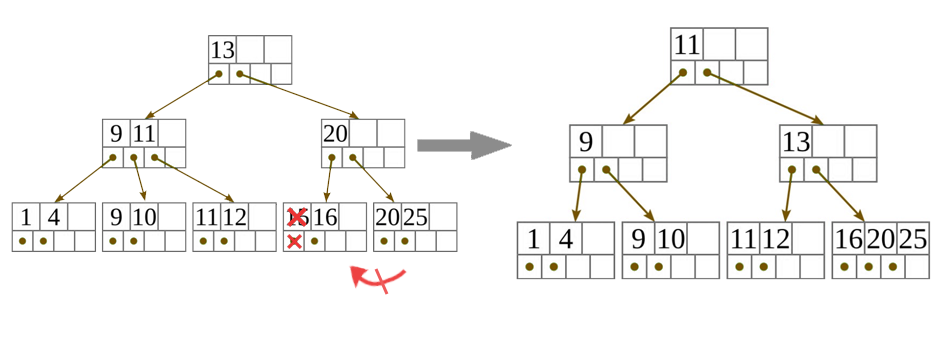
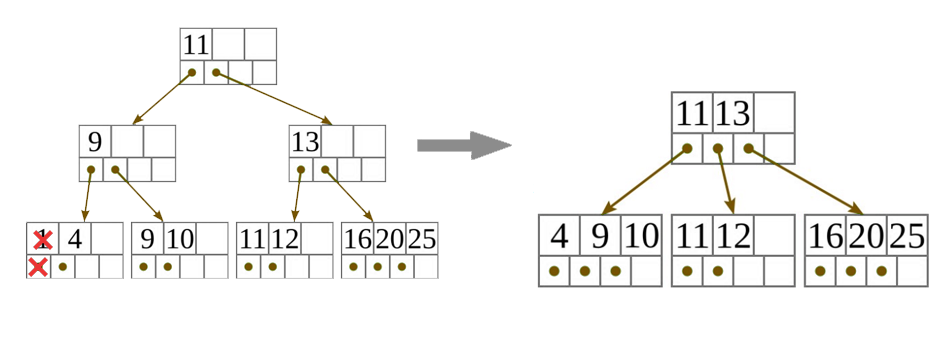
- Ha a belső csúcsnak már túl kevés gyereke van ahhoz, hogy teljesítse az invariánst, és a következő, valamint a megelőző testvére is a minimumon van, hogy teljesítse az invariánst, akkor egyesítsük egy vele szomszédos testvérével! Az egyesített csúcsot a két testvér közül a (balról jobbra sorrend szerinti) elsőből hozzuk létre. Gyerekei és hasító kulcsai először a saját gyerekei és hasító kulcsai az eredeti sorrendben, amiket a két testvér közti (a közös szülőjükben lévő) hasító kulcs követ, és végül a második testvér gyerekei és hasító kulcsai jönnek, szintén az eredeti sorrendben. Ezután töröljük a második testvért. A két testvér egyesítése után meg kell ismételnünk a törlő algoritmust a közös szülőjükre, hogy eltávolítsuk a szülőből a hasító kulcsot (ami eddig elválasztotta a most egyesített testvéreket), a most törölt második testvérre hivatkozó mutatóval együtt.
Törlés a gyökércsúcsból, ha az nem levél:
- Töröljük a gyökércsúcs éppen most egyesített két gyereke közti hasító kulcsot és az egyesítés során törölt gyerekére hivatkozó mutatót a gyökércsúcsból!
- Ha a gyökércsúcsnak van még 2 gyereke, kész vagyunk.
- Ha a gyökércsúcsnak csak 1 gyereke maradt, akkor töröljük a gyökércsúcsot, és a megmaradt egyetlen gyereke legyen az új gyökércsúcs! (Ekkor a B+ fa magassága csökken.)
Animáció
Az animáció fejlesztés alatt áll 😭😭
Leírás
Feladatok
Az alábbi feladatok a gyakorlatokon elvégzendő kötelező, illetve gyakorló feladatok.