Alapfogalmak:

Egyszerű gráf:

Gráf alatt egy $G = (V, E)$ rendezett párost értünk, ahol $V$ a csúcsok tetszőleges, véges halmaza, $E \subseteq V \times V \setminus \{(u, u) : u \in V \}$ pedig az élek halmaza. Ha $V = \{\}$, akkor üres gráfról, ha $V \neq \{\},$ akkor nemüres gráfról beszélünk. Kizárjuk a párhuzamos- és hurokéleket, ezekkel nem foglalkozunk.

Irányítatlan gráf:

A $G = (V, E)$ gráf irányítatlan, ha tetszőleges $(u, v) \in E$ élre $(u, v) = (v, u)$.

Irányított gráf:

A $G = (V, E)$ gráf irányított, ha tetszőleges $(u, v),(v, u) \in E$ élpárra $(u, v) \neq (v, u)$. Ilyenkor azt mondjuk, hogy az $(u, v)$ él fordítottja a $(v, u)$ él, és viszont.

Út:

A $G = (V, E)$ gráf csúcsainak egy $< u_{0}, u_{1}, . . . u_{n}>$ $(n \in N)$ sorozata a gráf egy útja, ha tetszőleges $i \in 1..n$-re $(u_{i-1}, u_{i}) \in E$. Ezek az $(u_{i-1}, u_{i})$ élek az út élei. Az út hossza ilyenkor $n$, azaz az utat alkotó élek számával egyenlő.

Kör:

A kör olyan út, aminek kezdő és végpontja (csúcsa) azonos, az út hossza $> 0$, és az élei páronként különbözőek.

Körmentes gráf:

Körmentes gráf alatt olyan gráfot értünk, amiben csak körmentes utak vannak.

Ritka gráf:

Egy gráf ritka gráf, ha $| E |$ sokkal kisebb, mint $| V |^2$.

Sűrű gráf:

Egy gráf sűrű gráf, ha $| E |$ megközelíti $| V |^2$ -et.

Összefüggő gráf:

Az irányítatlan gráf összefüggő, ha tetszőleges csúcsából bármelyik csúcsába vezet út. Az irányított gráf összefüggő, ha az irányítatlan megfelelője összefüggő.

Gráfábrázolások:

Grafikus ábrázolás és szöveges ábrázolás:

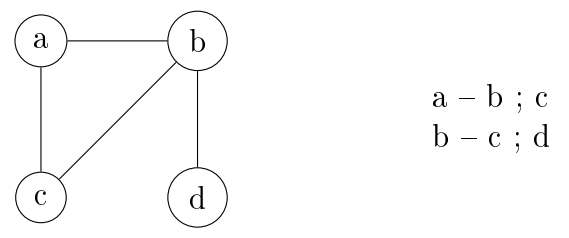
Irányítatlan: Felsoroljuk a csúcs szomszédait, ( $a - b ; c$ ). Fontos, hogy az élek csak egyszer szerepelnek, tehát, ha van $a - b$, akkor már nem kell $b - a$. Ez azért van, mert az irányítatlan gráf definíciója szerint, tetszőleges $(u, v) \in E$ élre igaz, hogy $(u, v) = (v,u)$.

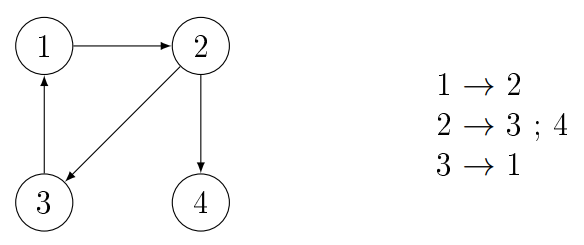
Irányított: Nyíllal elválasztva felsoroljuk a csúcsok rákövetkezőit ( $a \rightarrow b ; c$ ).

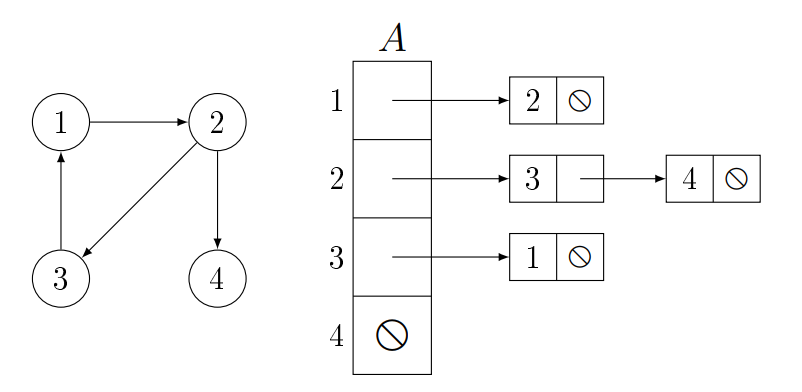
Szomszédossági listás (Éllistás):

A gráfot egy $A/1 : Edge^*[n]$ pointertömb segítségével ábrázoljuk. $A[i]$ egy S1L, ami tartalmazza a $v_i$ csúcs szomszédait vagy rákövetkezőit. A csúcsokat növekvően írjuk le konvenció szerint. Az $Edge$-nek van egy $v$ adattagja, ami a csúcs értékét tartalmazza és van egy $next$ adattagja, ami a következő csúcsra mutató pointer.

$Edge$

$+v: \mathbb{N}$ $+next: Edge^*$

Irányítatlan gráf esetében $A[i]$ egy S1L, ami tartalmazza a $v_i$ csúcs szomszédait. Fontos kiemelni, hogy a szöveges ábrázolással szembe, itt le kell írni az oda-vissza utakat is, tehát a listák hosszainak összege $2\cdot|E|$ lesz. Irányított gráf esetében a szomszédsági listák hosszainak összege $|E|$. A szomszédossági listás ábrázoláshoz szükséges tárterület mérete $\Theta (V + E)$.

A szomszédsági listás ábrázolás hátránya, hogy nehéz eldönteni, szerepel-e egy él a gráfban, hiszen ehhez az S1L-ben kell keresni. Ez a hátrány kiküszöbölhető csúcsmátrix használatával, ez azonban aszimptotikusan növeli a szükséges tárterület méretét. A szomszédsági listákon alapuló ábrázolást inkább ritka gráfokra használjuk.

Szomszédossági mátrixos (Csúcsmátrixos):

Egy $A/1 : bit[n, n]$ mátrix reprezentálja, ahol $n = |V|$, tehát a csúcsmátrix mérete $|V|\times|V|$. Mivel ez egy bit mátrix, ezért vagy $0$-ás vagy $1$-es lehet csak benne:

• $0$ jelenti azt, hogy nincs él a két csúcs között, $A[i, j] = 0 \iff (v_i , v_j ) \notin E$.
• $1$ jelenti azt, hogy van él a két csúcs között, $A[i, j] = 1 \iff (v_i , v_j ) \in E$.

A csúcsmátrix $\Theta (V^2)$ tárterületet foglal le, függetlenül a gráf éleinek számától.

Irányítatlan esetben elég lenne csak az alsó vagy felső háromszögmátrixot ábrázolni, mivel a főátlóra szimmetrikus. Ezzel majdnem felére csökkenthetjük az ábrázoláshoz szükséges tárterület méretét. A főátlóban mindig $0$-ák vannak, mivel nem foglalkozunk hurokélekkel.

Ennek az ábrázolásnak nagy előnye, hogy $\Theta (1)$ alatt eldönthető, hogy egy él benne van-e a gráfban, $(v_i, v_j) \in E$. A csúcsmátrixos ábrázolás előnyösebb lehet sűrű gráfok esetén.

Tárigény:

A szomszédsági listák együttesen aszimptotikusan kevesebb tárterületet igényelnek, mint a csúcsmátrix, azonban a használat során hatékonyságban ugyanennyivel elmaradnak attól, így ha a gráf mérete nem túl nagy, akkor kedvezőbb a hatékonyabb és egyszerűbb csúcsmátrixos ábrázolást használni.