Alapfogalmak:

Élsúlyozott gráf:

Élsúlyozott gráf alatt egy $G = (V, E)$ gráfot értünk a $w : E \rightarrow \mathbb{R}$ súlyfüggvénnyel, ahol $V$ a csúcsok tetszőleges, véges halmazát jelöli, $E$ pedig az élek halmazát, $E \subseteq V \times V \setminus \{ (u, u) : u \in V \}$. (Kizárjuk a párhuzamos- és hurokéleket, ezekkel nem foglalkozunk.)

Út hossza:

Élsúlyozott gráfban az út hossza az út mentén található élek összsúlya.

Gráfábrázolások:

Grafikus ábrázolás és szöveges ábrázolás:

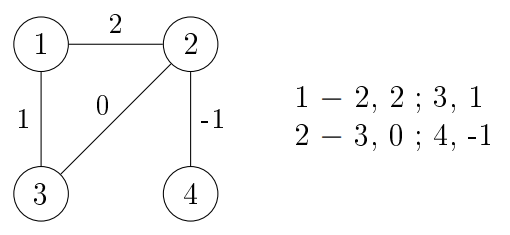
Irányítatlan: Felsoroljuk a csúcs szomszédait pontosvesszővel elválasztva, viszont vesszővel elválasztva mellé írjuk a szomszédjához vezető él súlyát, ( $a - b,1 ; c,2$ ). Fontos, hogy az élek csak egyszer szerepelnek, tehát, ha van $a - b,2$, akkor már nem kell $b - a,2$.

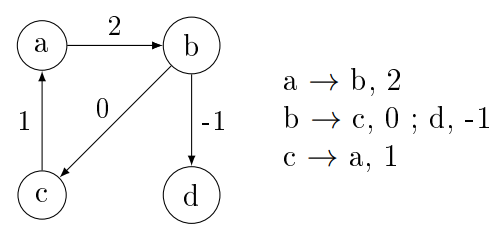
Irányított: Nyíllal elválasztva felsoroljuk a csúcsok rákövetkezőjét az élek súlyával együtt. ( $a \rightarrow b,4 ; c,2$ ).

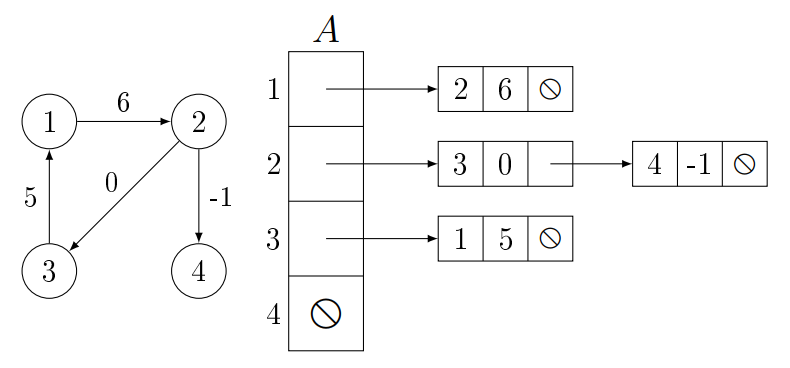
Szomszédossági listás (Éllistás):

A gráfot egy $A/1 : Edge^*[n]$ pointertömb segítségével ábrázoljuk. $A[i]$ egy S1L, ami tartalmazza a $v_i$ csúcs szomszédait vagy rákövetkezőit. A csúcsokat növekvően írjuk le konvenció szerint. Az $Edge$-nek van egy $v$ adattagja, ami a csúcs értékét tartalmazza és van egy $next$ adattagja, ami a következő csúcsra mutató pointer. Továbbá van egy $w$ adattagja is, ami a két csúcs közti él súlyát fogja tárolni.

$Edge$

$+v: \mathbb{N}$ $+w : \mathbb{R}$ $+next: Edge^*$

Irányítatlan gráf esetében $A[i]$ egy S1L, ami tartalmazza a $v_i$ csúcs szomszédait. Fontos kiemelni, hogy a szöveges ábrázolással szembe, itt le kell írni az oda-vissza utakat is, tehát a listákban összesen $2\cdot|E|$ darab él lesz. Irányított gráf esetében a szomszédsági listák hosszainak összege $|E|$. A szomszédossági listás ábrázoláshoz szükséges tárterület mérete $\Theta (V + E)$.

A szomszédsági listás ábrázolás hátránya, hogy nehéz eldönteni, szerepel-e egy él a gráfban, hiszen ehhez az S1L-ben kell keresni. Ez a hátrány kiküszöbölhető csúcsmátrix használatával, ez azonban aszimptotikusan növeli a szükséges tárterület méretét. A szomszédsági listákon alapuló ábrázolást inkább ritka gráfokra használjuk.

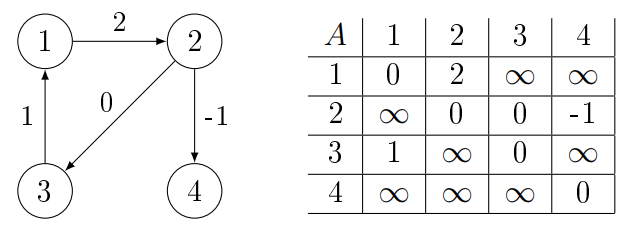
Szomszédossági mátrixos (Csúcsmátrixos)

Egy $A/1 : \mathbb{R}_\infty [n, n]$ mátrix reprezentálja, ahol $n = |V|$.

• $\infty$ jelenti azt, hogy nincs él a két csúcs között, $A[i, j] = \infty \iff (v_i , v_j ) \notin E \land i \neq j$.
• $0$ jelentheti azt, hogy az él súlya $0$, ha $i \neq j$.
• $0$ jelentheti azt, hogy a csúcsból önmagába $0$ költségű úton érünk el, ha $i = j$.
• $\mathbb{R}$ jelenti a két csúcs közti él súlyát, $A[i,j] = w(v_i, v_j) \iff (v_i, v_j) \in E$.

A csúcsmátrix $\Theta (V^2)$ tárterületet foglal le, függetlenül a gráf éleinek számától. Irányítatlan esetben elég lenne csak az alsó vagy felső háromszögmátrixot ábrázolni, mivel a főátlóra szimmetrikus. A főátlóban mindig $0$-ák vannak, mivel nem foglalkozunk hurokélekkel és a csúcsból önmagába $0$ költség alatt érhetünk el.

Ennek az ábrázolásnak nagy előnye, hogy $\Theta (1)$ alatt eldönthető, hogy egy él benne van-e a gráfban, $(v_i, v_j) \in E$. A csúcsmátrixos ábrázolás előnyösebb lehet sűrű gráfok esetén.

Tárigény:

A szomszédsági listák együttesen aszimptotikusan kevesebb tárterületet igényelnek, mint a csúcsmátrix, azonban a használat során hatékonyságban ugyanennyivel elmaradnak attól, így ha a gráf mérete nem túl nagy, akkor kedvezőbb a hatékonyabb és egyszerűbb csúcsmátrixos ábrázolást használni.