A szélességi keresés az egyik legegyszerűbb gráfbejáró algoritmus, és ezen alapul sok fontos gráfalgoritmus. Prim minimális feszítőfákra adott algoritmusa és Dijkstra legrövidebb utat meghatározó algoritmusa a szélességi kereséshez hasonló gondolatmenetet használ.

Adott irányított vagy irányítatlan, összefüggő vagy nem összefüggő gráf és egy kitüntetett $s$ kezdő csúcs esetén a szélességi keresés módszeresen megvizsgálja a gráf éleit, és így rátalál minden $s$-ből elérhető csúcsra. Emellett kiszámítja az összes $s$-ből elérhető csúcsba a távolságot, azaz a legkevesebb élt tartalmazó utatat (optimális utatat). Ha több ilyen van, akkor az egyiket. Tehát lehetnek olyan csúcsok és élek, amelyeket nem érint az algoritmus.

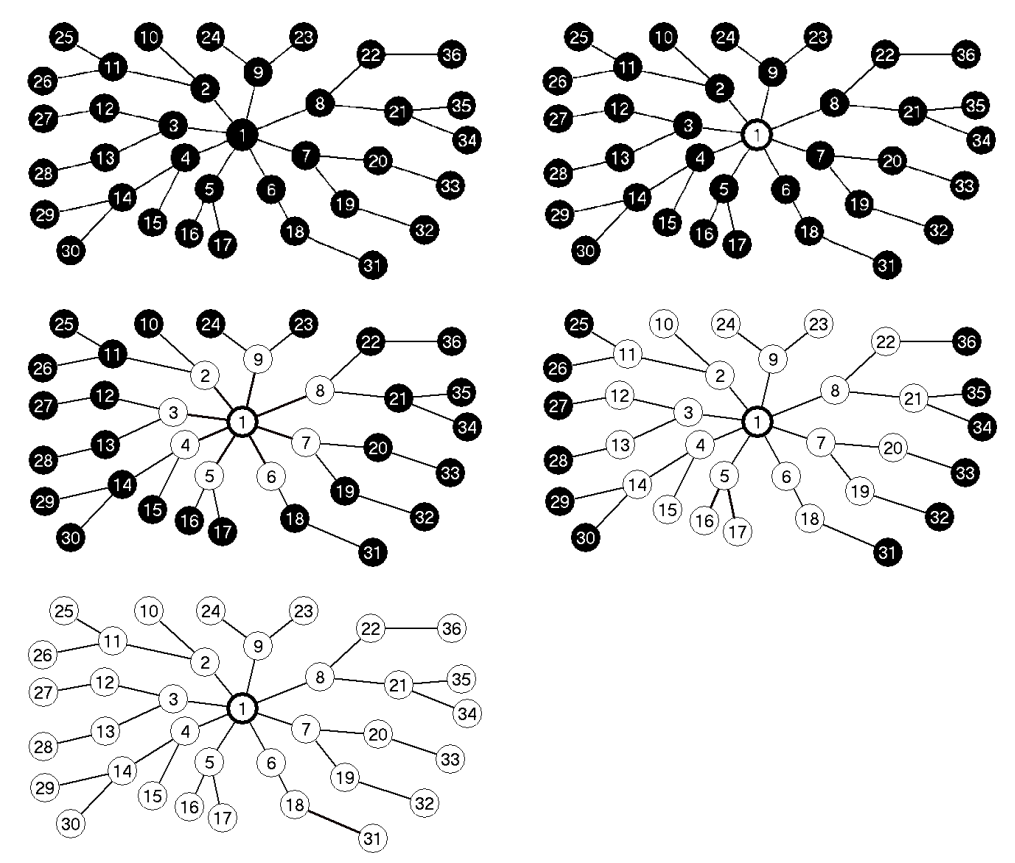
A szélességi keresés elnevezés onnan ered, hogy az algoritmus a már elért és a még felfedezetlen csúcsok közötti határvonalat egyenletesen terjeszti ki a határ teljes széltében. Minden szintet teljesen feldolgoz, mielőtt a következőre lépne, közben pedig éppen a következő szinten levő csúcsokat találja meg.

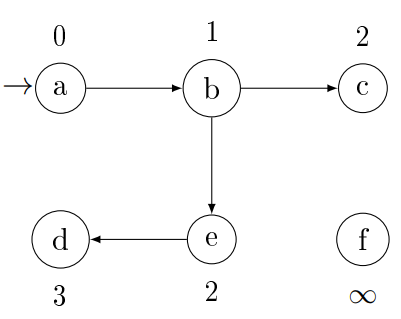
Az algoritmus:

A csúcsokat címkékkel látjuk el:

• $d$ hány élen keresztül jutottunk el a csúcsba (optimális út hossza)
• $\pi$ melyik csúcsból jutottunk el hozzá (szülő csúcs)

Ha a kezdő csúcsból nincs út $u$ csúcsba, akkor $d(u) = \infty$ és $\pi(u) = \emptyset$. A kezdő csúcsra mindig igaz lesz, hogy $\pi(s) = \emptyset$.

A bejáró algoritmusok, hogy ne „körözzenek” gyakran színezést használnak. Így nem „látogathatunk meg” többször egy csúcsot. A szélességi keresés a csúcsok színezésével tartja számon a bejárás pillanatnyi állapotát:

• fehér felfedezetlen csúcs (kezdetben mindegyik fehér)
• szürke feldolgozás alatt álló csúcs (megtalált/elért, de még fel nem dolgozott csúcs)
• fekete feldolgozott csúcs

Egy fekete csúcs összes szomszédja elért csúcs (szürke). A szürke csúcsoknak lehetnek fehér szomszédaik. Ezek alkotják az elért és a még felfedezetlen csúcsok közötti határt.

A végeredmény egy általános fa lesz, amit szélességi fának és legrövidebb utak fájának is nevezünk, mivel az $s$-ből elérhető csúcsokra a legrövidebb utakat tartalmazza.

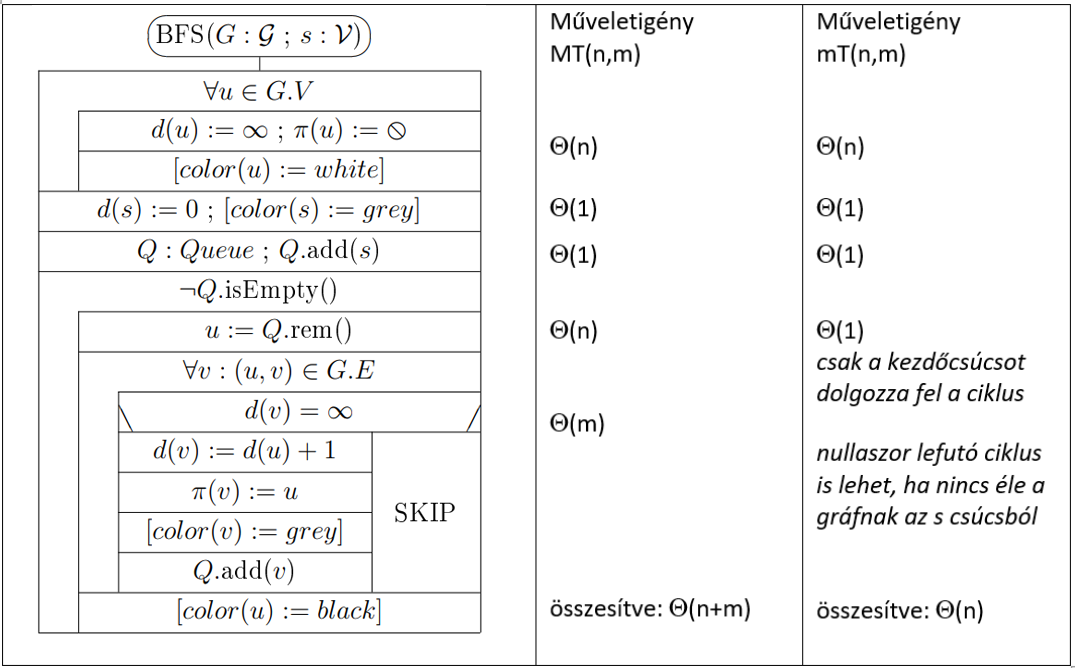
Működése:

Az első ciklus inicializálja a csúcsok címkéit, ($d(u) = \infty$ ; $\pi(u) = \emptyset$). Azokat a csúcsokat, amiket már elértünk (szürke), de még a gyerekeit nem néztük meg a $Queue$-ba kerülnek. Így az elején a kezdő csúcs is belekerül. A második ciklus addig fut, amíg van még fel nem dolgozott elem. Kiveszünk egy elemet és beállítjuk a gyerekeit, ($d(v) := d(u) + 1$ ; $\pi (v) := u$). Ha a gyerekénél a $d(u) \neq \infty$, akkor már korábban találtunk hozzá optimális utat, tehát az else ág fut le. A ciklus leáll, ha minden a kezdő csúcsból elérhető csúcsot feldolgoztunk.

Absztrakt gráf típus:

A szélességi bejárást és nagyon sok másik algoritmust is egy absztrakt gráf típussal fogunk ábrázolni. Ebben az absztrakt gráf típusban megadjuk a csúcsainak absztrakt típusát ($\mathcal{V}$, vertex) és az élek absztrakt típusát ($\mathcal{E}$, edge). Egy él megadja a két csúcsot, amelyet összeköt.

$\mathcal{E}$

$+ u, v: \mathcal{V}$

Ezek alapján be tudjuk vezetni az élsúlyozatlan absztrakt gráfot is ($\mathcal{G}$, graph). Ez a gráf típus tartalmazza az élek halmazát ($E$), a csúcsok halmazát ($V$) és egy metódust, amely megadja egy adott csúcs összes szomszédját ($A$).

$\mathcal{G}$

$+ V: \mathcal{V} \{\}$ $+ E: \mathcal{E} \{\} \space // \space E \subseteq V \times V \setminus \{ (u,u) : u \in V \}$ $+ A: V \rightarrow 2^{V} \space // \space A(u) = \{ v \in V \mid (u,v) \in E \}$

Műveletigény:

• $n = |G.V|$ (csúcsok száma), $m = |G.E|$ (élek száma)
• $MT(n, m) \in \Theta(n+m)$
• $mT(n, m) \in \Theta(n)$

Gyakorlati alkalmazása:

Ezen alapul sok fontos gráfalgoritmus: Prim algoritmusa, Sor-alapú Bellman-Ford algoritmus. Dijkstra algoritmusa is hasonló gondolatmenetet használ.