A versenyek kiemelt célja a tehetséggondozás, a tehetségek felismerése, az adott iskola tanárától független, objektív számonkérés.
Az évek során sokféle verseny keletkezett. Kezdetben csak programozási versenyek voltak, de abból is volt sokféle variáció: számítógépes – számítógép nélküli, egyéni verseny – csapatverseny, háromtusa verseny (informatika-fizika-matematika), kéttusa verseny (informatika alkalmazói-matematika), stafétaverseny. A programozási versenyekkel egyidőben jelentek meg a programtermék versenyek. Sokkal később követték ezeket az alkalmazói versenyek. [TSz]
Magyarországon egy 1983-as próbálkozás után 1985-ben kezdődött az országos informatika versenyek sorozata. Ugyanekkor indult például Bulgáriában és Szlovákiában is. Németországban kicsit ennél is régebben kezdődtek az informatikai versenyek. A világ országai nagyon nagy részét azonban évekkel előztük meg.
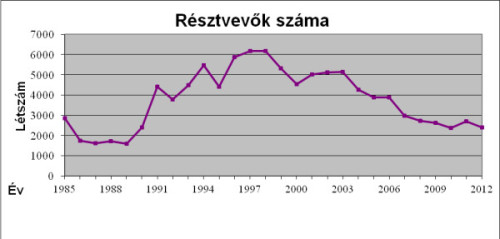A progranozási verseny résztvevői számának alakulása 2012-benSok éven keresztül programozási versenyről beszélhettünk (Nemes Tihamér OKSzTV), három korcsoportban: 5-8., 9-10., illetve 11-12. osztályos tanulóknak. Az országos versenyek mindig 3 fordulósak: iskolai, regionális és országos fordulóval.
Az első fordulóban 200 pontot lehet szerezni, a második és harmadik fordulóban pedig 150-150 új pontot, valamint az előző forduló pontszáma 25%-át.
A diagram érdekes jellemzője (de most nem témánk), hogy az induló versenyzők létszáma erős korrelációban áll a közoktatásban ajánlott, vagy kötelező informatika tanórák számával.
Az 1989-ben kezdődött International Olympiad in Informatics és az 1994-ben indult Central-European Olympiad in Informatics miatt 1989-től a programozási versenyrendszer egy negyedik fordulóval, az olimpiai válogatóversennyel bővült. [IOI,CEOI,OV]
Körülbelül ebben az időben indult több más regionális verseny, pl. Balkan Olympiad in Informatics, illetve Baltic Olympiad in Informatics.
A Logo programozási nyelv széleskörű elterjedése miatt (bekerült a Nemzeti Alaptantervbe, illetve a Comenius Logo több száz iskolába eljutott) 1998-ban indult a Logo programozási verseny. Ez az évek során 4 korcsoportra tagozódott: 3-4., 5-6., 7-8., illetve 9-10. osztályos tanulóknak (a Nemes Tihamér versenyhez hasonlóan iskolai, regionális és országos fordulóval).
A mellékelt diagramon látszik a gyors felfutás és a stabil 3500 körüli résztvevő szám.
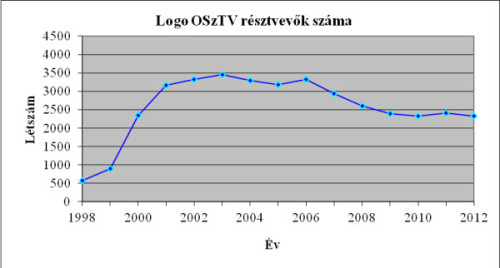A Logo verseny résztvevői számának alakulása 2012-benA verseny háromfordulós:
Az első fordulóban 100 pontot lehet szerezni, a második és harmadik fordulóban pedig 75-75 új pontot, valamint az előző forduló pontszáma 25%-át.
A programozási versenyek sikere után több évvel jelentek meg másfajta informatikai versenyek. Az 1995-ben indult budapesti alkalmazói verseny (rajzolás, szövegszerkesztés, táblázatkezelés, adatbázis-kezelés, honlapszerkesztés, prezentáció). A Nemes Tihamér verseny felső korcsoportja 2004-től Informatika OKTV, amin belül először volt országos alkalmazói tanulmányi verseny. A Nemes Tihamér versennyel együtt 2 korcsoportban rendezik, 9-10., illetve 11-12. osztályos tanulók számára.
A mellékelt diagramon látszik, hogy a résztvevők száma szinte pillanatok alatt túlszárnyalta a másik két verseny indulóinak létszámát.
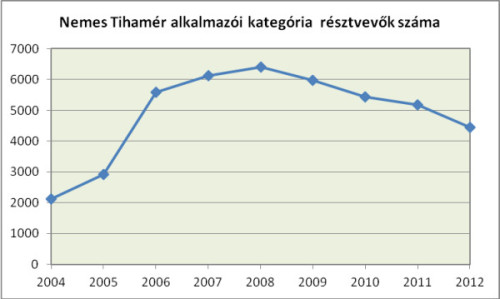Az alkalmazói verseny résztvevői számának alakulása 2012-benEz a verseny is háromfordulós:
Az első fordulóban 400 pontot lehet szerezni, a második és harmadik fordulóban pedig 300-300 új pontot, valamint az előző forduló pontszáma 25%-át.
Az iskolákban tartandó első fordulóban a tanulók analizáló képességét tesszük próbára számítógép használata nélkül: 6-10 kisebb feladatot (algoritmus- vagy programrészletet, működési vázlatot) adunk, és olyan kérdésekre várunk választ, mint pl. (1) mit csinál? (2) milyen hibák vannak benne? (3) milyen feltételek mellett működik? (4) mi hiányzik belőle? (5) mire használjuk a változókat? (6) megoldja-e a kitűzött feladatot? (7) mit tudunk a változók értékeiről? stb. Ebben a fordulóban számítógép nem használható.
Ez a feladattípus az egyes országok informatikai versenyein ritkaság. Jellemzően a 15-20 évvel ezelőtti versenyeken fordul elő (pl. Bulgária, Németország, Szlovákia). A magyar programozási versenyeken azonban mind a mai napig megmaradt. Ennek elsődleges oka nem a hagyomány, hanem az informatika oktatás célja. Úgy gondoljuk, hogy a mindenkinek szóló informatikában is szükség van algoritmizálási ismeretekre. Itt azonban az elsődleges cél az algoritmusok megértési és végrehajtási képessége. Tömeges verseny esetén emiatt ezt a képességet kell mérni a verseny első fordulójában. Valószínűleg hasonló céllal vannak jelen a Theoretical problems a litván olimpiákon is.
Hasonló az Australian Informatics Competition: Sample Questions, itt azonban a válaszok is megjelennek, tesztszerűen, és a versenyzőknek csak választani kell közülük.
E különlegesség miatt itt kicsit részletesebben foglalkozunk ezzel a feladattípussal.
Egyik lehetőség egy algoritmus működésével kapcsolatos kérdések feltétele. Ez elképzelhető úgy is, hogy nem adjuk meg, hogy az algoritmusnak mi a feladata. Ilyenkor kérdezhetjük azt, hogy adott bemenetre milyen eredményt kapunk (pl. First Bulgarian National Olympiad, Problem 2), illetve azt, hogy adott kimenet esetén mi lehetett a bemenet (pl. First Bulgarian National Olympiad, Problem 4).
A mi példánkban megmondjuk mi a feladat, majd kétféle kérdést teszünk fel:
A versenyekről vett példák szövegét dőlten szedve, keretezve közöljük.
Algoritmizálási versenyfeladat |
|---|
Az alábbi algoritmus két rendezett vektor (A, B) elemeiből állít elő egy újabb rendezett vektort, amelyben azok az elemek szerepelnek, amelyek legalább az egyikben előfordulnak. Az eredmény minden elemének különbözőnek kell lennie. ForráskódÖsszefuttatás(A,N,B,M,C,K):
I:=1; J:=1; K:=0
while I≤N and J≤M do
K:=K+1
if A(I)<B(J) then C(K):=A(I); I:=I+1
elif A(I)=B(J) then C(K):=A(I); I:=I+1; J:=J+1
else C(K):=B(J); J:=J+1
endif
endwhile
endproc.
(A) Milyen feltételeknek kell teljesülniük A-ra és B-re az eljárás helyes működéséhez? (B) Milyen hibát okoz az eredményben, ha ezek a feltételek nem teljesülnek? (C) Helyes működés esetén, rögzített N és M esetén milyen A és B vektorra a leggyorsabb, illetve a leglassúbb az algoritmus? |
Egy másik feladattípus esetén az algoritmust szövegesen közöljük, majd a megértését próbáljuk ellenőrizni. A lehetséges kérdések itt az adatokra vonatkozó invariáns állítással, a bemenet és a kimenet közötti összefüggéssel, az algoritmus végrehajtása befejeződésének feltételével kapcsolatosak.
Algoritmizálási versenyfeladat |
|---|
Egy dobozban fekete és fehér borsszemeket tárolunk. Véletlenszerűen kiveszünk 3 szemet. Ha mindhárom fekete, akkor nem teszünk semmit. Ha két fekete van köztük, akkor mind a hármat visszarakjuk. Ha két fehér van köztük, akkor a feketét visszarakjuk. Ha mindhárom fehér, akkor pedig egy fehéret rakunk vissza. Ha kettőnél több bors maradt, akkor a maradékra fenti algoritmus újra kezdődik. (A) Hogyan változik a fekete, illetve a fehér borsszemek száma az algoritmus végrehajtása során? (B) A borsszemek számának milyen lényeges tulajdonsága nem változik meg az algoritmus végrehajtása során? (C) Milyen kiinduló állapot esetén kerülhetünk végtelen ciklusba az algoritmus végrehajtása során? (D) Mitől függ, hogy a végén hány bors marad és azok milyen színűek? |
A harmadik példánkban egy adatstruktúra megértését, a vele dolgozó algoritmussal
Algoritmizálási versenyfeladat |
|---|
Egy vasútvonal két állomásán egy nap feljegyeztük, az összes, a másik felé áthaladó vonat indulási, illetve érkezési idejét. Feltételezzük, hogy a vonatok a vizsgált szakaszon nem előzhetik meg egymást és egymással szemben soha sem haladhat két vonat. N adatpárt ismerünk, mindegyike egy állomás sorszámot és egy időpontot tartalmaz, idő szerinti sorrendben. Ezek alapján a program találja ki, hogy melyik adatpárban van indulási és melyikben érkezési idő. (A) Mit ír ki az alábbi algoritmus? (B) Mi a Queue szerepe az algoritmusban? (C) Mi a szerepe a (*)-gal jelölt sornak? ForráskódSorInicializálás
while not eof? do
Olvas(állomás,time)
if empty?(Queue) then x:=állomás endif (*)
if állomás=x then Sorba(time) else Sorból(t); write(time-t) endif
endwhile
(D) Mi lesz a sor tartalma lépésenként a ciklusmag elején, ha az adatok a következők: (1,1),(1,3),(2,4),(1,4),(1,5),(2,5),(2,6),(2,7),(2,8),(2,9),(1,13),(1,14)? |
A következő példa nyelvek szintaktikai szabályainak megértését, a nyelvet generáló automata működésének megértését, a rekurzió fogalmának, a rekurzív kiszámítás módjának használatát kéri számon.
Algoritmizálási versenyfeladat |
|---|
A FURA nyelvben (a szokásos kettes számrendszer helyett) három jelet (A, B és C betű) használnak a szavak leírására. Mivel ez egy mesterséges nyelv, a szavakat szigorú szabályok betartásával hozzák létre.
(A) A FURA nyelv szavai-e az AC, ABBCC, ABCCC, ABBBBBB szavak? Amelyik igen, arra add meg, hogy milyen szabályok alkalmazásával kapható az ABB szóból! (B) Fogalmazd meg, milyen szabályoknak kell teljesülnie egy szóra, hogy a FURA nyelv szava legyen! |
Utolsó példánk pedig a dinamikus programozás elvének megértéséről, annak kézi kivitelezéséről szól.
Algoritmizálási versenyfeladat |
|---|
Egy karaktersorozat tükörszó, vagy palindrom, ha szimmetrikus, azaz ha balról jobbra és jobbról balra olvasva azonos. Például 2 karakter beszúrásával az S=„Ab3bd” karaktersorozat palindrommá alakítható („dAb3bAd” vagy „Adb3bdA” is lehet belőle). Kettőnél kevesebb karakter beszúrásával azonban ebből a karaktersorozatból nem állítható elő palindrom. Jelöljük M(i, j)-vel minden (i, j) 1≤i≤j≤N indexpárra, hogy az S[i..j]=S[i]...S[j] szó legkevesebb hány betű-beszúrással tehető tükörszóvá! (A) Add meg, hogy S=”FAKANÁL” esetén hogyan néz ki az M mátrix! (B) Adj képletet M(i, j) kiszámítására! |
A Nemzetközi Informatikai Diákolimpián egyszer történt kísérlet ilyen feladat kitűzésére, 1995-ben, Hollandiában, azóta az olimpiákon ezt a feladattípust senki sem támogatja. A mi feladataink ennél sokkal egyszerűbbek, rövidebbek, szélesebb versenyzői kör számára érthetőek.
A fentiekkel azt szeretnénk bemutatni, hogy az egyszerű algoritmus végrehajtási képességen túl ezek a feladatok alkalmasak programozási ismeretek bevezetésére, emiatt a tanítási folyamatban hatékonyan felhasználhatók.
A magyar verseny második fordulójában három-öt kisebb, konstruáló, szintetizáló jellegű feladatot kell megoldani; a rendelkezésre álló idő 5 óra. Csak a futási eredményt értékeljük, nem pedig a megírt program szövegét. Súlyt helyezünk arra, hogy a versenyzők pontosan betartsák a specifikációt, ne csak tartalmilag, hanem formailag is legyenek előírás szerintiek az eredmények. Ebben a fordulóban korcsoportonként 200-300 versenyző szerepel.
Ez a feladattípus már lényegében megfelel a nemzetközi informatikai olimpiákon használt feladatoknak, van azonban több, lényeges különbség.
A korcsoportonként szervezett versenyben fokozatosan kell eljutni a diákolimpiák feladattípusaihoz.
A legkisebbeknek olyan feladatokat kell megoldani, amelyben néhány elemi adatból kell valamit kiszámítani.
Elemi programozási versenyfeladat |
|---|
Az időt (óra, perc, másodperc, századmásodperc) formában tároljuk. Olyan típusú kérdéseket szeretnénk feltenni, hogy ha most 8 óra 10 perc 12 másodperc 3 századmásodperc van, akkor mennyi lesz az idő 80 másodperc múlva, illetve hogy mennyi volt az idő ezelőtt 2 óra 15 perccel. Azaz az idő típusú adatokra el kell készíteni az összeadás és a kivonás műveletet. Készíts programot, amely beolvas egy időpontot: O, P, MP, SZMP formában (0≤O≤23, 0≤P≤59, 0≤MP≤59, 0≤SZMP≤99), majd egy idő távolságot (0≤A, 0≤B, 0≤C, 0≤D) és kiírja, hogy mennyi volt az idő A óra B perc C másodperc D századmásodperccel korábban, illetve későbben! |
Hasonló probléma (Third Millenium) található a XI. Lithuanian Olympiads in Informatics olimpián, a juniorok második fordulójában. E feladattípus jellemzője, hogy csupán a megoldás helyességével kell törődni, hatékonysági szempontokra itt még nem gondolunk.
A második és a harmadik korcsoportban részben elemi algoritmusokkal foglalkozunk.
Ennek fontos jellemzője, hogy a magyar informatika érettségi vizsgán is ilyen jellegű feladatok fordulnak elő, a verseny erre kiváló előkészítést jelent.
Az alábbi feladat egy intervallum-sorozat uniójának kiszámításáról szól.
Elemi programozási versenyfeladat |
|---|
Egy kiállítás három napon keresztül folyamatosan nyitva tart éjjel-nappal. A látogatóknak előre meg kellett venniük a jegyet, mégpedig úgy, hogy meg kellett mondaniuk, hogy mikor érkeznek, és mikor távoznak a kiállításról. A kiállítás szervezői így pontosan tudják, hogy mikor nem lesz senki a kiállításon. Azt tervezik, hogy csak azokra az időszakokra biztosítanak személyzetet, amikor lesz látogató. Készíts programot, amely kiszámítja azokat az időintervallumokat, amikor személyzetet kell biztosítani! |
A másik feladattípus ismert, nevezetes algoritmusok alkalmazását igényli, az alábbi például egy terület befestését.
Nevezetes algoritmus alkalmazása |
|---|
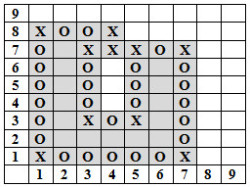 Egy négyzet alakú területre egy befestett sokszöget rajzoltunk, amelynek oldalai párhuzamosak a képernyő szélével. Készíts programot, amely megadja, hogy hány képpontból áll a sokszög! Az ábrán X jelöli a sarokpontokat, O a határvonalakat, s szürkére festettük a sokszöghöz tartozó összes pontot. |
Több olyan feladat is előfordul, amelyek előkészítik a komolyabb algoritmusokat. Az alábbi feladat egy irányított gráffal kapcsolatos kérdéseket tesz fel, de közülük csak a harmadikhoz szükséges gráfbejárás, az első kettő tulajdonképpen adott tulajdonságú pontokat keres a gráfban.
Gráfos versenyfeladat |
|---|
Egy csapatversenyben N csapat vesz részt, a csapatokat 1 és N közötti sorszámukkal azonosítjuk. Ismerjük M mérkőzés eredményét, bármely két csapat legfeljebb kétszer játszhat egymással. Írj programot az alábbi feladatokra! (A) Adj meg két csapatot, amelyek már legyőzték egymást! (B) Add meg azokat a csapatokat, akik már játszottak, de még senki nem győzte le őket! (C) Adj meg egy csapatot, amely „közvetve legyőzte magát” (azaz pl. A ilyen, ha A legyőzte B-t, B legyőzte C-t, ..., Y legyőzte Z-t és Z legyőzte A-t)! |
Bár ezen feladatok némelyikénél a hatékonyság is számíthatna, ebben a fordulóban lényegében nem foglalkozunk ezzel. Az adatok mennyisége ugyanis vagy nagyon kicsi, vagy a legrosszabb megoldási ötletek esetén is viszonylag gyors megoldást kaphatunk. Ebben az esetben, amely program 1 percen belül nem ad megoldást, az majdnem biztos, hogy 1 napon belül sem.
A harmadik fordulóban a feladatok típusa lényegében nem változik; a rendelkezésre álló idő 6 óra. Itt korcsoportonként 50-80 versenyző szerepel. A versenyzők itt is 1 perces időlimitet kapnak, ez azonban már alkalmas az exponenciális és a polinomiális algoritmusok megkülönböztetésére.
Itt már a 9-10. osztályosok feladatai is részben megfelelnek a diákolimpiákon előforduló feladatoknak, a 11-12. osztályosoké pedig csak ilyen típusú. Nem használjuk azonban még az összes lehetséges feladattípust. Jellemező erre a fordulóra a különböző gráf-algoritmusok használata, mint az alábbi, mélységi bejárásra épülő példából látszik:
Gráfos versenyfeladat |
|---|
A városi vidámpark több részlegből áll. Az egyes részlegeket kétirányú utak kötik össze. Az úthálózat olyan, hogy bármely részlegtől legfeljebb három közvetlen út vezet más részleghez, kivéve a főbejáratot tartalmazó részleget, onnan legfeljebb két másik részleghez vezet közvetlen út. Egy részleghez érve csak a részlegen keresztül lehet másik útra lépni. Minden részleghez el lehet jutni – esetleg más részlegeken keresztül – a főbejáratot tartalmazó részlegtől. Minden részlegbe csak az oda szóló belépőjeggyel lehet bemenni. Kedvezményesen lehet venni olyan belépőjegy köteget, amely minden részlegbe pontosan három jegyet tartalmaz. Készíts programot, amely kiszámít egy olyan séta útvonalat, amely a főbejáratot tartalmazó részlegtől indul, oda ér vissza és minden részleget tartalmaz, de minden részleget legfeljebb háromszor! |
Sok esetben nem gráf a feladat hátterében lévő adatstruktúra, hanem fa. Itt az alapvető egyszerű rekurzív bejárások mellett érdekes például a C részfeladat:
Gráfos versenyfeladat |
|---|
Egy titkos társaság hierarchikusan épül fel, minden tagja csak a felettesét és a hozzá közvetlenül beosztott legfeljebb két tagot ismeri. A társaságnak pontosan egy olyan tagja van, akinek nincs főnöke. Bármelyik tag küldhet levelet bármelyik tagnak. Azonban minden levél csak úgy juthat el a feladótól a címzetthez, hogy egy lépésben vagy a közvetlen főnökhöz, vagy közvetlen beosztotthoz továbbítódik. Írj programot, amely adott két, X és Y tagra kiszámítja az alábbi kérdésekre adandó választ! (A) Hány beosztottja – nem csak közvetlen – van az X és az Y tagnak? (B) Hány lépéssel továbbítódik egy levél, ha X küld levelet Y-nak? (C) Mennyi a legkevesebb lépésszám, ami alatt biztosan odaér egy levél, bárki legyen is a feladó, illetve a címzett? |
Minden évben szerepel a mohó stratégia, a fiatalabb korosztály általában olyan feladatot kap, amely emlékeztet valamelyik 1-2 évvel korábbi diákolimpiai, illetve olimpiai válogatóversenyes feladatra:
Mohó stratégiás versenyfeladat |
|---|
Egy népszerű zenekar a következő évre vonatkozó fellépéseit tervezi. Sok meghívása van fellépésre, ezek közül kell a zenekarnak választani, hogy melyeket fogadja el. Minden fellépés pontosan egy napot foglal el. Minden beérkezett meghívási igény egy (e, u) számpárral adott, ami azt jelenti, hogy az igénylő azt szeretné, hogy a zenekar olyan k sorszámú napon tartson nála koncertet, hogy e≤k≤u. A zenekarnak az a célja, hogy a lehető legtöbb fellépése legyen. Készíts programot, amely kiszámítja, hogy mely meghívásokat fogadja el, hogy a következő évben a lehető legtöbb fellépése legyen, és a programod adjon is meg egy beosztást! |
A diákolimpiai válogatóversenyen körülbelül 25-30 versenyző vesz részt, közülük kerül ki az IOI-s és a CEOI-s csapat 4-4 tagja. Alapelvünk, hogy az IOI-s csapatba 11-12. osztályos, a CEOI-s csapatba pedig 9-11. osztályos tanulók kerülhetnek, ezzel is szeretnénk lehetőséget biztosítani a fiatalabb korosztálynak a nemzetközi megmérettetésre.
E verseny feladattípusai, értékelési szempontjai, időlimitjei szó szerint azonosak az informatikai diákolimpiákkal. Határozott eltérés több diákolimpiától, hogy a feladatok jelentős részében van részfeladat, amelyre külön pontok szerezhetők. A tesztesetek kiválasztása is eltér a diákolimpiai feladatokétól. Erre mutat példát a következő, speciális minimális feszítőerdő megadását kérő feladat, és annak értékelése:
Minimális feszítőfás versenyfeladat |
|---|
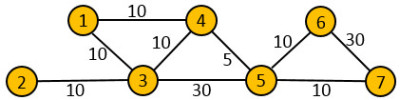 A Malomipari Vállalat K malomban őröl és csomagol lisztet. A lisztet N városba kell elszállítani úgy, hogy a szállítási összköltség a lehető legkisebb legyen. Írj programot, amely megadja a minimális szállítási költséget, illetve minden városra, hogy oda melyik malomból kell szállítani a lisztet! Értékelés: Minden városban van malom (0+1 pont) Sehol nincs malom (1+0 pont) Egyetlen malom, mindenhova van közvetlen út (0+1 pont) Egyetlen malom, több lépéses utak is vannak (1+1 pont) Egyetlen malom, nem a legrövidebb éleket kell választani (1+1 pont) Több malom, a legrövidebb éleket kell választani (1+1 pont) Több malom, nem a legrövidebb éleket kell választani (1+1 pont) Több malom, nem összefüggő gráf, minden komponensben van malom (1+1 pont) Több malom, nem összefüggő gráf, nem megoldható (1+0 pont) Véletlen közepes teszt (1+1 pont) Véletlen közepes teszt (1+1 pont) Véletlen nagy teszt (2+2 pont) Véletlen nagy teszt (2+2 pont) |
Az értékelésből látszik, hogy az egyszerű speciális esetek megoldását is pontozzuk. Másik jellemző, hogy elég sok pontot lehet szerezni a nem optimális megoldásokkal is, csak az utolsó 4 teszt különíti el az optimális megoldásokat (bár 12 pontot érnek a lehetséges 26-ból).
A továbbiakban csak az új feladattípusokat nézzük át. Az elmúlt években az informatikai diákolimpiákon gyakran megjelennek a kombinatorikus feladatok, emiatt az olimpiai válogatásunkon is szükség van rá:
Kombinatorikai versenyfeladat |
|---|
A processzorgyártó cégek megállapodtak abban, hogy milyen rendszert alkalmaznak az általuk gyártott processzorok azonosítására. Minden cég kap egy betűkészletet, és ezekből kell az azonosító kódot képeznie úgy, hogy minden betű pontosan egyszer szerepeljen az azonosítóban. Például egy cég azt kapta, hogy minden azonosítója egy-egy ’a’, ’b’, ’c’, ’d’ és ’x’ betűt tartalmazzon. A processzorok a gyártási sorrendben ábécé szerint növekvően kapják mindig a következő azonosítót. Készíts programot, amely adott azonosítóra kiszámítja a következő két kérdésre a választ. (A) Hányadik a gyártási sorrendben a processzor? (0-tól sorszámozva) (B) Mi az ábécé sorrendben rákövetkező szabályos azonosító? |
Szintén jellemző feladatok a diákolimpiákon az interaktív feladatok osztályába tartozó
Interaktív versenyfeladat |
|---|
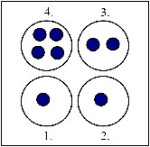 A Mancala családba tartozó játékok, amelyeket kavicsokkal és üregekkel játszottak, a legősibbek közül valók. A mini mancala változatában, amely kétszemélyes játék, négy üreg van. Az 1. és a 2. üreg az egyik, a 3. és 4. üreg a másik játékoshoz tartozik. A játék kezdetén az üregekbe véletlenszerűen beraknak legfeljebb 8 kavicsot. A játékosok felváltva lépnek, az 1-es játékos kezd. A soron következő játékos kiválaszt a hozzá tartozó üregek közül egyet, majd kiveszi az abban lévő összes kavicsot. Ezután a kivett kavicsokból egyet eldob, a többit pedig kavicsot szétosztja az üregek között az alábbiak szerint. Az órajárással ellentétes irányban haladva minden érintett üregbe rak egy kavicsot, de kihagyja azt az üreget, amelyből kivette a kavicsokat. Például, ha az 1. üreget választja, amiben 6 kavics van, akkor sorrendben a 2., 3., 4., 2. és 3. üregbe rak egy-egy kavicsot. A játék akkor ér véget, ha a soron következő játékos nem tud lépni, mert mindkét hozzá tartozó üreg üres. Az a játékos nyer, aki utoljára tudott lépni. Írj programot, amely a játékot kezdő 1. játékos nyerő stratégiáját valósítja meg! |
2008 körül jelentek meg hangsúlyozottan a geometriai feladatok, amelyek azonban a diákolimpiai szokásoknak megfelelően csak egész aritmetikára építve is megoldhatók:
Geometriai versenyfeladat |
|---|
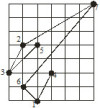 Adott a síkon egy P ponthalmaz és két kitüntetett pontja; a és b. Kiszámítandó egy olyan a-ból b-be vezető, nem-metsző törtvonal, amelynek csúcspontjai pontosan a P ponthalmaz elemei. A pontokat a 1,...,N számokkal azonosítjuk. Egy ilyen törtvonal megadható a pontok azonosítóinak egy olyan felsorolásával, amelyben az első elem a, az utolsó b, továbbá az egymást követő pontokat kötjük össze egyenes szakaszokkal. Írj programot, amely kiszámít egy a-ból b-be vezető, nem-metsző törtvonalat! |
Összefoglalóan nézzük meg, milyen feladattípusokat használunk az egyes korosztályok versenyein: [HGyZsL1, HGyZsL2, ZsL1, ZsL3, NP, TÁZsL]
Korosztály | Feladattípus |
|---|---|
5-8. osztály | Ciklus nélküli feladatok, számlálás, keresés, rendezés, kiválogatás, maximum-kiválasztás, unió, metszet, szimuláció, szövegelemzés, szövegformázás, speciális rendezések, egyszerű online algoritmusok, kis elemszámú sorozatok feldolgozása. |
9-10. osztály | Geometriai algoritmusok, intervallumokkal, halmazokkal kapcsolatos algoritmusok, rekurzió, fákkal kapcsolatos rekurzív algoritmusok, gráfok elemzése, elemi gráfalgoritmusok, backtrack, grafikai alapalgoritmusok, mohó stratégia, dinamikus programozás, adatstruktúrák alkalmazása, szövegformázás, szövegelemzés, bitminták elemzése, szimuláció, speciális struktúrák bejárása, online algoritmusok, feladatmegoldás automatákkal. |
11-12. osztály | Gráfbejárás, feszítőfák, szövegfeldolgozás (tömörítés, keresés), automaták, kombinatorikus algoritmusok. |
Olimpiai válogatóverseny | Az előző feladattípusokon túl: Kombinatorikus algoritmusok, interaktív feladatok, kétszemélyes játékok nyerő stratégiája, feladatmegoldás speciális „gépekkel”. |
A fenti táblázatból látszik, hogy a feladattípusokban nagy ugrás az első két korcsoport határán van. A többi korcsoportban, illetve versenyeken a feladatok témakörei azonosak, csupán a konkrét feladatok nehézsége különböző.
Például a 9-10. osztályosok gráfokkal kapcsolatos algoritmusaiban a legbonyolultabb egy egyszerű gráf-bejárás. Az egyszerűbb gráfos feladataik a gráfok elemzésével megoldhatók (pl. egy pontnak hány bemenő éle van, hány kimenő éle van, elágazásmentes láncok felfedezése a gráfban, ...).
A 11-12. osztályosoknál ezzel szemben már a legegyszerűbb feladatnál is szükség van gráf-bejárásra, minimális költségű feszítőfa előállítására, ... A válogatóversenyen pedig ugyanezen feladattípusok esetén sokkal fontosabb a hatékony megoldás, a megfelelő adatstruktúra választása, ...
Vannak ezen kívül speciális versenyek, ahol a feladattípusok is eltérhetnek a fentiektől.
A zalaegerszegi Zrínyi Miklós Gimnázium 1992 óta évente megrendezi a matematika, fizika, és számítástechnika tárgyköreit egyaránt felölelő, komoly díjazású versenyét, az Izsák Imre Gyula Természettudományi Versenyt. [IIGy]
A verseny 1993 óta a gimnázium egykori tanulójának, a zalaegerszegi születésű matematikus-csillagásznak, Izsák Imre Gyulának – emlékét őrizve – viseli a nevét.
1992-ben a meghívásos versenyen három megye gimnazistái mérhették össze tudásukat. 1993-ban és 1994-ben már tágabb régió – Dunántúl minden megyéjéből, illetve Budapestről egy-egy gimnázium – diákjait hívták meg. 1995-ben – a Zrínyi Miklós Gimnázium 100 éves jubileumi ünnepségsorozata keretében – pedig az egész országra kiterjedt a meghívottak köre.
A versenyzők mindhárom tantárgyból – az OKTV-n elfogadott szabályok szerint – két-két órás feladatsort oldanak meg. A számítástechnika versenyen a tanulók IBM PC gépen dolgozhatnak Pascal, C vagy BASIC nyelven. Ezen a versenyen mind a három tantárgy a saját feladatain túl olyan feladatokat is ad, amelyek a másik tantárgyhoz kapcsolódnak. Így szerepelt például olyan fizikai feladat, amelyben a fizikai tudás alapján kellett meghatározni egy CD maximális lehetséges kapacitását.
Az informatikai feladatok egy része a fizikához, más része a matematikához kapcsolódik. Ilyen például a következő feladat:
Fizikához kapcsolódó versenyfeladat |
|---|
Egy gömböt úgy tudunk a síkban ábrázolni, hogy a felénk forduló részét fényesebbre festjük, mint a kevésbé felénk fordulókat. A fényesség a fény beesési szögének koszinuszával arányos. A fényességet úgy állítjuk be, hogy a legfényesebb helyeken nagyon sűrűn teszünk a sötét háttérre fehér pontokat, s minél kisebb a fényesség, annál ritkábban. Ha a gömböt a nézőpontból egy párhuzamos fény-nyalábbal világítjuk meg, akkor a jobboldali ábrán látható képet kapjuk. Ha a fény-nyalábot a nézőponthoz képest az y-tengely körül 60 fokkal elforgatjuk jobbra, akkor a baloldali ábrán látható képet kapjuk. Készíts programot, amely beolvassa a fény-nyaláb és a nézőpont által bezárt szöget, majd kirajzolja a megvilágított gömböt úgy, hogy a határvonalát piros körrel rajzolja!
|
Matematikához kapcsolódó versenyfeladat |
|---|
Egy pozitív racionális számot a következő alakban írhatunk fel: 2 1/3, azaz megadhatjuk az egészrészét, a törtrésze számlálóját és nevezőjét. A nevező 0 érétkű nem lehet. Írj programot, amely két ilyen számot beolvas, majd kiírja az összegüket, és a szorzatukat! Ha szükséges, az eredményben egyszerűsíts, a törtrészt ne írd ki, ha a számláló 0, az egészrészt ne írd ki, ha az 0 lenne, kivéve, ha a törtrész is 0! Példák:  |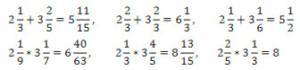
2013-ban kísérletképpen a versenyt matematika-számítástechnika kategóriában is megrendezték, ahol a számítástechnika alkalmazói ismereteket (rajzolás, szövegszerkesztés, táblázatkezelés) jelent.
Az 1. iskolai forduló feladatai egy részét papíron kapják a versenyzők, amelyeket számítógép nélkül kell megoldaniuk. Ezek nagyobb része Logo programok megértésével kapcsolatos, az alábbi típusú kérdésekre keresi a választ:
Számítógép nélküli Logo versenyfeladat |
|---|
A következő ábrákat az alábbi eljárás rajzolta: Forráskódtanuld négyzet :h
ismétlés 4 [előre :h jobbra 90]
vége
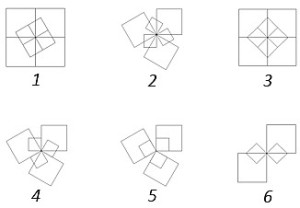 Az eljárást hatféleképpen hívtuk meg: (A) ismétlés 6 [négyzet 100 jobbra 60 négyzet 50 jobbra 60] (B) ismétlés 6 [négyzet 100 jobbra 120 négyzet 50 jobbra 120] (C) ismétlés 6 [négyzet 100 jobbra 45 négyzet 50 jobbra 45] (D) ismétlés 6 [négyzet 100 jobbra 45 négyzet 50 jobbra 135] (E) ismétlés 6 [négyzet 100 balra 30 négyzet 50 jobbra 120] (F) ismétlés 6 [négyzet 100 jobbra 30 négyzet 50 jobbra 90] Párosítsd össze az eljáráshívásokat a nekik megfelelő rajzokkal! |
Ugyanez a típus egy, a 4. korcsoportnak szánt feladatban:
Számítógép nélküli Logo versenyfeladat |
|---|
Mi az eredménye alábbi a függvénynek, ha :s értéke: (A) ”alma (B) ”körte (C) ”eper (D) ”dió (E) ”barack Forráskódeljárás a :s
ha üres? :s [eredmény [hamis hamis]]
ha egyik első :s [eredmény lista "igaz
utolsó a elsőnélküli :s]
ha másik első :s [eredmény lista első a elsőnélküli :s "igaz]
eredmény a elsőnélküli :s
vége
eljárás egyik :s
eredmény eleme? :s "aáoóuú
vége
eljárás másik :s
eredmény eleme? :s "eéiíöőüű
vége
(F) Az a függvény lehetséges eredményei hogyan függnek a paraméterétől? (Milyen típusú paraméterre milyen eredményt kapunk?) |
Más feladatokban Logo-hoz hasonló automaták vezérlését kell követni:
Logo-szerű gondolkodás versenyfeladat |
|---|
Kövesd az autó útját a városban, ha az e jelenti az előre egy egységet, a b a balra 90-et és a j a jobbra 90-et. eee bee jee eej eee bee jee  |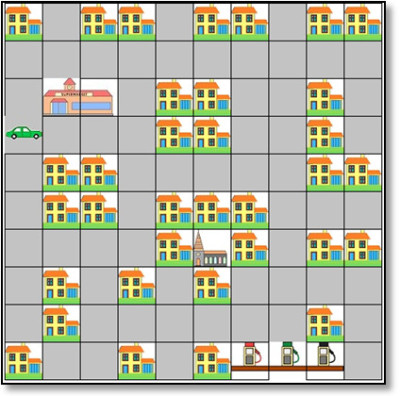
Az első fordulóban itt számítógépes feladatok is szerepelnek, elsősorban különböző sokszögek, körök, körívek rajzolására alapozva:
Logo programozási versenyfeladat |
|---|
Készítsd el az alábbi zászlókat rajzoló Logo eljárásokat (Mikronézia :h, Grenadine :h,Skócia :h, Bahrein :h)! A zászlók magassága 2*:h, szélessége 3*:h. Mikronézia szélessége 4*:h. Ami különböző színűnek (színárnyalatúnak) látszik, azt különböző színekkel kell rajzolni!  |
A feladatok itt sokszor az elsőre gondoltnál egyszerűbben, pl. tollvastagság állításával oldhatók meg:
Logo programozási versenyfeladat |
|---|
Készítsd el az alábbi piktogramokat! Használd a tollvastagság beállítását!  |
A második fordulóban megjelennek a rekurzív ábrák:
Logo programozási versenyfeladat |
|---|
Egy fa az ábrának megfelelően növekszik. Az :n-edik lépésben az :n-1-edik fa különböző darabjaiból újabb ágak nőnek ki, feleakkora ághosszal. Készítsd el a fát rajzoló eljárást (fa :n :h), ahol :h az 1 lépésbeli ághossz!  |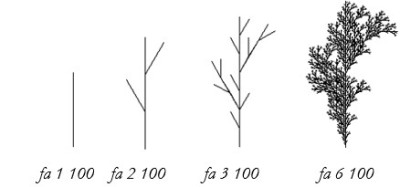
Maradnak természetesen a sokszög-variációk:
Logo programozási versenyfeladat |
|---|
Egyes szabályos sokszögek körberakhatók kétféle, ugyanolyan oldalhosszúságú szabályos sokszöggel. Készítsd el a sok1 :méret,sok2 :méret és sok3 :méret eljárásokat, ahol a :méret paraméter a sokszögek oldalhosszát határozza meg!  |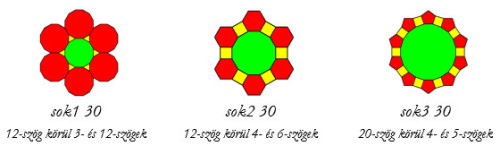
Tipikus feladatok itt a mozaikok:
Logo programozási versenyfeladat |
|---|
Egy mozaikot háromféle alapelemből építünk fel (elem1 :h,elem2 :h,elem3 :h), ahol :h az alapelemek köré írható négyzet oldalának hossza. Az alapelemek sorokba rendezhetők (sor1 :m :h,sor2 :m :h,sor3 :m :h), ahol a sorok :m*2+3 darab alapelemet tartalmaznak. A sorok felépítése az ábrán látható. Sorok alkalmas egymás mellé helyezésével készíts mozaikot (mozaik :m :h), amelynek belsejében :m*2+3 sorban soronként :m piros négyzet található! A mozaik közepén lévő kereszteket, zöldre színezzük!  |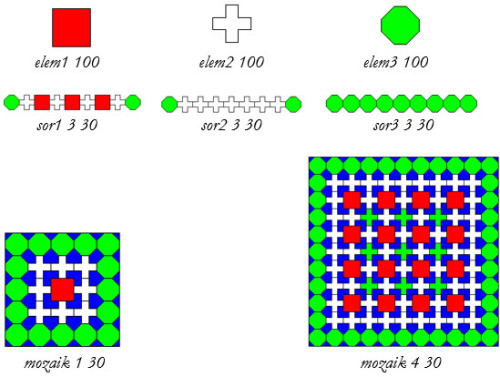
Szükség lehet vagy megfelelő matematikai ismeretekre, vagy ezt pótló Logo-programozás technológiai ismeretekre:
Logo programozási versenyfeladat |
|---|
Az alábbi három ábrához (ábra1 :n :h,ábra2 :n :h,ábra3 :n :h) szükség van koordináta-tengelyekre, melyeken :n darab :h hosszúságú egység szerepel. A beosztásokat az ábrának megfelelően kötjük össze. A második ábra az elsőből 2, a harmadik pedig 4 darabot tartalmaz. Készítsd el a három ábrarajzoló eljárást!  |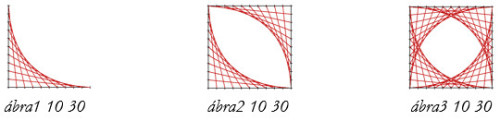
A harmadik fordulóban a területkitöltés sokszor nem ismétléssel, hanem forgatással keletkezik (további jellemző, hogy amit a versenyzők nem tudhatnak, abban segítséget kapnak). AZ alábbi példa a legidősebbeknek szólt:
Logo programozási versenyfeladat |
|---|
Készíts Logo eljárást (üveg :n :r) :n cikkből álló ablaküveg készítésére, ahol :r a cikkek sugara (a leghosszabb szakasz végpontjának távolsága a piros kör középpontjától)! Segítség: az :sz szöget bezáró T hosszú szakaszok végpontjának távolsága: 2*T*sin :sz/2  |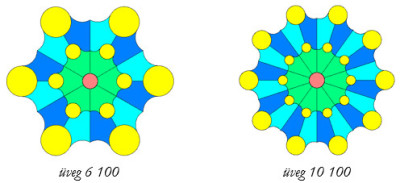
Grafikus feladatok szöveggel paraméterezhetők lesznek. Ezt már a 7-8. osztályosoknak is tudni kell:
Logo programozási versenyfeladat |
|---|
Verne Gyula Sándor Mátyás című regényében egy olyan titkosírást használnak, amelyben egy 6x6-os négyzetrácsos lap bizonyos mezőit kivágják (ezt hívják rostélynak), majd egy ugyanilyen négyzetes elrendezésben szereplő betűtáblázat fölé helyezve a látható betűket folyamatosan kiolvassák. Készíts Logo eljárást (rostély :paraméter), amely egy pozícióival megadott rostélyt kirajzol! Az ábrán látható rostélyt az alábbi paraméterekre kapjuk: rostély [[2 4 6][5][3][2 5][6][4]]  |
A legnagyobbaknak pedig megjelennek a tisztán szöveges feladatok is:
Logo programozási versenyfeladat |
|---|
Készíts Logo függvényt (kinyert :pakli :húzások), amely egy 21-est játszó párosnál megadja, hogy ki nyert. A 21-es kártyajátékot magyar kártyával játsszák. Először mindenki kap két lapot, majd felváltva húznak, amíg kérnek. A lapok értéke 2,3,4,7,8,9,10,11 lehet, a figurák zöld, szív, makk és tök. A :pakli listában a kártyák értékeit találjuk. A :húzások listában az egymás után következő húzásokhoz tartozó személyek azonosítója áll. Pl. [A A B B] azt jelenti, hogy 2 alkalommal A kapott lapot a pakliból, majd kettőt B is kap. Ha valaki lapjainak az összege 21-nél több, az vesztett („befuccsolt”), egyébként az nyer, aki lapjainak nagyobb az értéke. Kinyert [M2 Z3 T7 S2 S10 M3 T4 ] [A A B B A B] eredménye A lapjainak értéke: 15, B lapjainak értéke: 12, tehát A nyert.  |
Összefoglalóan nézzük meg, milyen feladattípusokat használunk az egyes korosztályok versenyein: [HBVZsL1,HBVZsL2,ZsL2,L]
Korosztály | Feladattípus |
|---|---|
3-4. osztály | A Logo nyelv grafikai utasításainak ismerete. A Logo-szerű gondolkodásmód, Logo-szerű algoritmusok megértése és végrehajtása. Elemi és összetett alakzatok megrajzolása, eljárások használata, eljárások paraméterezése. Ábrák eltolása, nagyítása, elforgatása. Sokszögek, csillagok, körök, körívek rajzolása. Sorminták, mozaikok rajzolása. Zárt területek befestése. |
5-6. osztály további tudnivalói | Logo-szerű tervezési ismeretek. Rekurzív ábrák (fák, indák, spirálok, fraktálok) rajzolása. Mozaikok rekurzívan. Teknőc visszavezetése korábbi helyére. |
7-8. osztály további tudnivalói | Érzékelős teknőc alkalmazása. A Logo nyelv rajzolási és szövegkezelési lehetőségeinek összekötése: szöveges paraméterrel vezérelt rajzolás. |
9-10. osztály további tudnivalói | A Logo nyelv szövegkezelő függvényei, alkalmazásuk szövegfeldolgozási feladatokban. |
Ezen a versenyen a többiektől határozottan eltérő feladatok fordulnak elő. Ezek jellege erősen gyakorlati, viszonylag egyszerű algoritmusokat kell használni egy-egy komplex feladat megoldásában. Itt ezért fontosabb a feladatok jó felbontása részfeladatokra, majd a részfeladatok megoldásainak helyes összeépítése.
A következő feladat tulajdonképpen nagyon hasonlít a diákolimpiák interaktív feladataira. Egy adatsorozaton kell egy adott ablakot csúsztatni, miközben a csúsztatás szabályait a menet közben bármikor érkező műveletek módosíthatják. Ezen a versenyen kézi értékelés volt, a képernyőn megjelenő tartalom alapján. Az automatikus értékelés a kimenet célszerű megfogalmazásával kicsit nehezen, de megoldható.
Egy kvázi interaktív feladat |
|---|
Készíts programot egy N vágányt tartalmazó vasútállomás elektronikus információs táblájának kezelésére! Az információs táblán jelenjen meg az állomás neve, az aktuális idő, valamint N sorban az induló és érkező vonatok adatai kétféle változatban:
A kétféle megjelenítés között a program felhasználója választhat tetszőleges időpontban. A tábla kezeléséhez szükséges adatokat a vasútvonal teljes menetrendjét tartalmazó állományban tároljuk. Bármikor érkezhet az adott időpont után érkező vonatokra vonatkozó üzenet – lehetséges, hogy a menetrendhez képest késnek. Az állomásfőnök bármikor megváltoztathatja a vonatok indulási idejét, illetve érkezésüket megelőzően a hozzájuk rendelt vágánysorszámot. Készíts programot az információs tábla kezelésére! |
Ez a verseny – sajnos – több éve megszűnt.
  |
 |
 |
A tananyag az ELTESCORM keretrendszerrel készült
