A fizikai szimulációban foglalkozunk statisztikus mechanikával. Vizsgáljuk molekulák eloszlását különböző feltételek mellett, az energia eloszlását kristályokban, makroszkopikus jellemzőket (pl. nyomás, entrópia), gázok és folyadékok viselkedését.
Nem célunk új fizikai ismeretek közlése, mivel ezek – véleményünk szerint – megtalálhatók az irodalomjegyzékben felsorolt színvonalas művekben. Nem cél továbbá nehéz matematikai módszerek bemutatása sem, hiszen ezekkel matematikusoknak kell foglalkozni, az ilyen területeken az együttműködés a célszerű út és mi ezt szeretnénk támogatni.
Úgy gondoljuk, hogy itt közölt modelljeinket felhasználva ezután már Olvasóink is tudnak további modelleket készíteni, amelyek remélhetőleg segítséget nyújtanak a fizika oktatásában.
Fizikai vizsgálatainkat egy olyan témakörrel kezdjük, amely megfelelő alapot adhat későbbi kémiai, biológiai, meteorológiai stb. modellek kialakításához.
Alapfeladatunk a következő lesz: adott valahány elemi rész (atom, ion, molekula), ismerjük ezek egyedi tulajdonságait, kölcsönhatásaikat (mikroszint), s azt szeretnénk megvizsgálni, hogy ezek az anyaghalmazok együttesen hogyan viselkednek, milyen – minőségi, mennyiségi – tulajdonságok jellemzőek rájuk, mint „egészre” (makroszint).
Az első kérdés, amelyre figyelmünket fordítjuk, így hangzik: ha ezen részecskék mozgását semmi sem befolyásolja, akkor hogyan töltik ki a rendelkezésre álló teret?
Képzeljünk el egy egyszerű kísérletet! Van két dobozunk, amelyekbe „darazsakat” (elemi részeket) zártunk. A darazsak a két doboz között véletlenszerűen röpködnek. Vizsgáljuk meg, milyen lesz hosszú idő alatt a darazsak eloszlása a két dobozban! Nagyon egyszerű algoritmust kapunk: a véletlenszerű röpködést úgy oldjuk meg, hogy kiválasztunk véletlenszerűen egy darazsat és azt áttesszük a másik dobozba.
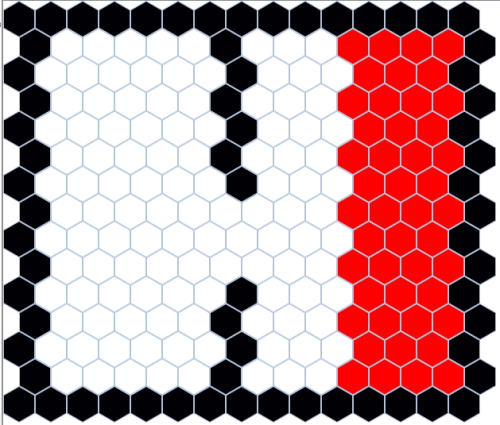A képen két, egymás melletti doboz látszik,az egyik félig töltve molekulákkal.
A képen látszik, hogy a kezdetben egy oldalon elhelyezkedő molekulák egyenletesen oszlanak el.Jelölje N a darazsak számát, D(i) pedig azt, hogy az i. darázs melyik dobozban van! Az A tartalmazza az 1. dobozban levő darazsak aktuális számát, S(i) pedig azt, hogy hányszor volt az 1. dobozban éppen i darab darázs. A folytonos keretmodellt fogjuk használni, mivel a darazsak nem megkülönböztethetők, s így ok-okozati probléma nem vethető föl a pszeudopárhuzamosság kapcsán.
Diffúzió:
i:=véletlen(N)
Ha D(i)=1 akkor D(i):=2; A:=A-1
különben D(i):=1; A:=A+1
S(A):=S(A)+1
Eljárás vége.
Ezzel az egyszerű programmal megfigyelhetjük, hogy
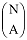
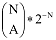
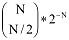
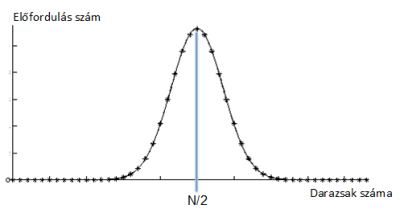Darazsak eloszlása az első dobozban.Figyeljük meg, hogy modellünk lényegében azonos a szimuláció alapjaiban tárgyalt 2. elemi modellel! A következő párhuzamokat érdemes észrevenni:
Ezek alapján nem meglepő, hogy tetszőleges kezdőállapotból kiindulva, a fele-fele arány lesz a végállapot, a darazsak száma ezen érték körül fog ingadozni.
Vizsgáljuk meg a problémát egy másik szemszögből! Egy lépésben minden darázsról döntsük el, hogy helyben marad, vagy pedig átrepül a másik dobozba! Adjuk meg az átrepülés valószínűségét (P)! (Az az eset számunkra nem érdekes, amikor a darazsak biztosan nem repülnek át a másik dobozba (P=0), s az sem, amikor biztosan átrepülnek (P=1)). Mivel itt egy lépés alatt minden darázzsal történik valami, ezért ezt a modellt a diszkrét keretmodellre építjük, az Új táblázat készítése eljárást írjuk meg. (Az előző modellben definiált objektumokat használjuk itt is.)
Diffúzió:
Ciklus i=1-től N-ig
Ha véletlenszám<P akkor D(i):=3-D(i)
Ciklus vége
A:=A darazsak száma az 1. dobozban
S(A):=S(A)+1
Eljárás vége.
Programunk használatával azt a tapasztalatot szűrhetjük le, hogy a binomiális eloszlás kialakulása mindenképpen bekövetkezik, a P paraméter csupán ennek sebességét befolyásolja (P=1/2 esetén a leggyorsabb, kis (de nem 0) vagy 1-hez közeli (de nem 1) értékekre pedig lassú).
Bonyolítsuk eredeti modellünket: ne 2, hanem M db dobozt helyezzünk egymás mellé! Minden darázs átrepülhet egy szomszédos dobozba (balra, illetve jobbra) egyenlő eséllyel. Vizsgáljuk így a darazsak eloszlását! Módosítjuk az eddig használt objektumokat: A(K) jelölje a K. dobozban levő darazsak aktuális számát, D(i) és N ugyanaz, mint korábban volt, M pedig legyen a dobozok száma. Ismét a folytonos keretmodellt használjuk. Eredményként, pl. 4 doboz esetén, ilyesfélét szeretnénk látni:
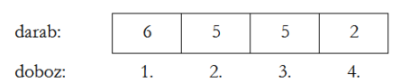
Diffúzió:
i:=véletlen(N)
Ha véletlenszám<0.5 akkor Balra(i) különben Jobbra(i)
Eljárás vége.
Balra(i):
Ha D(i)>1 akkor A(D(i)):=A(D(i))-1; D(i):=D(i)+1; A(D(i)):=A(D(i))+1
Eljárás vége.
Jobbra(i):
Ha D(i)<M akkor A(D(i)):=A(D(i))-1; D(i):=D(i)+1; A(D(i)):=A(D(i))+1
Eljárás vége.
Kísérleti tapasztalataink azt mutatják, hogy a darazsak egyenletes eloszlása a legvalószínűbb. (Az egyes dobozokat külön-külön vizsgálva, itt is a 2. elemi modell (S-,S+) feltételei teljesülnek, ami stabilitásra utal.)
Vegyük észre, hogy itt egy egydimenziós véges bolyongási feladatot vizsgálunk, amelyben egyszerre – egymástól függetlenül – több pont mozoghat. Ez a folyamat a matematikailag jól leírt problémák közé tartozik, úgyhogy nagyon sok helyen találkozhatunk vele.
Igen egyszerűen lehet az előbbi modellt síkbelivé általánosítani, ezért mi az Olvasóra hagyjuk ezt az adaptációs feladatot. (Ezt annál is inkább megtehetjük, mivel éppen ezt tesszük majd meg a következő fejezetben.)
Az eddigi modellek vizsgálata alapján (a következő fejezet első modellje is alátámasztja majd ezt) megadhatjuk a korábban föltett kérdésre a választ: ha az atomok, molekulák mozgását semmi sem befolyásolja, akkor a rendelkezésükre álló teret egyenletesen töltik ki, térrészenkénti eloszlásukra pedig a binomiális eloszlás a jellemző. (Vegyük észre a síkbeli variáns egy furcsaságát: a sík szokatlan geometriájú, hiszen az (i,j) ponttól az (i-1,j) , illetve az (i-1,j-1) pont azonos távolságra vannak (8-szomszédos esetben); de 4-szomszédos esetben sem tökéletes, bár nem azonos a távolsága az oldalnál, illetve sarkon elhelyezkednek.)
Ezek a modelljeink leírják a diffúzió jelenségét gázokban. Felhívjuk a figyelmet arra, hogy ezek jól közelítik például a szabad elektronok eloszlását a semleges fémekben is.
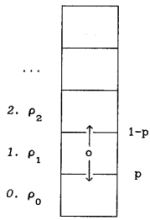
Vizsgáljuk meg, mi történik, ha a molekulák mozgására hat a gravitáció! (A molekulák eloszlását vizsgáljuk például a légkörben.) Az új hatást úgy vesszük figyelembe, hogy a molekulák teljesen véletlenszerű sebességéhez hozzáadunk egy lefelé irányuló komponenst, azaz így a molekulák nagyobb valószínűséggel mozoghatnak lefelé. Az egydimenziós diffúziós modellt alakítjuk át, melyben most a hely indexe a magasságot jelöli. Minden egyes kiválasztott molekula P valószínűséggel mozduljon el lefelé (P>1/2) és 1-P valószínűséggel felfelé. (M a dobozok, N a molekulák száma.)
Diffúzió gravitációs térben:
i:=véletlen(N)
Ha véletlenszám<P akkor Lefelé(i) [alias Balra]
különben Felfelé(i) [alias Jobbra]
Eljárás vége.
Az eredmény megjelenítését 5 doboz esetén a következőképpen képzeljük el:
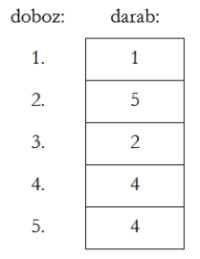
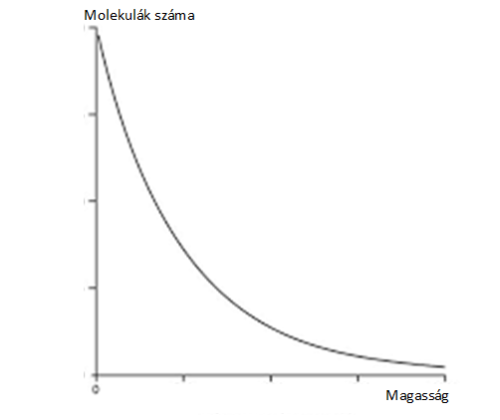A molekulák eloszlása magasság függvényében.Ez nem is meglepő; hiszen az egyensúly miatt a 0. változatlanságát fejezi ki:
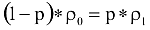
Az 1. változatlanságát fejezi ki:
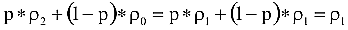
így
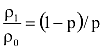
és
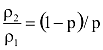
Ez – könnyen láthatóan – általában is igaz, amiből már következik, hogy
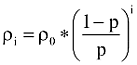
valamint alkalmasan választott c (ln((1-p)/p) esetén:
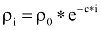
A lefelé és felfelé elmozdulás valószínűsége látható.Az eredmény igazolja hétköznapi tapasztalatunkat, amely szerint a légkör a magassággal „rohamosan” csökken. Precízebben fogalmazza meg ugyanezt a tudomány az ún. barometrikus magasságformulával:
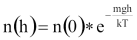
Ebből következőleg a szimulációban adott időtartam alatt minden dobozhatáron azonos a lefelé és a felfelé átlépők száma:
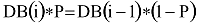
azaz
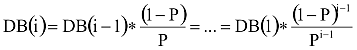
Ez a modell a 2. elemi modellre (S-,S+) épül, mégsem egyenletes eloszlást kapunk eredményül. Ez azonban nem ellentmondás: ez az elemi modell ugyanis csak a stabilitást, azaz a végállapot – statisztikus – létét garantálja, az egyenletességet pedig csak abban az esetben, ha a változás kétféle jelensége (születés, halálozás) azonos valószínűségű. Ebben a gravitációs modellben a dobozokba való be-, illetve kilépés helytől függően más-más esélyű, ami kizárja az egyenletes eloszlást.
Hatszög teret alkalmazva, ha változatni tudjuk a fel/le lépés valószínűségét, a következő állapothoz juthatunk:
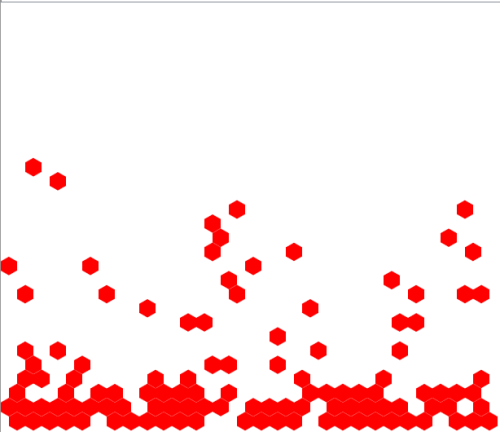Gravitációs modell.Amennyiben modellünket vízszintesen ható erővel is kiegészítjük, akkor a kialakuló felszín mutatja a két erő hatása következtében elvárt ferde egyenest:
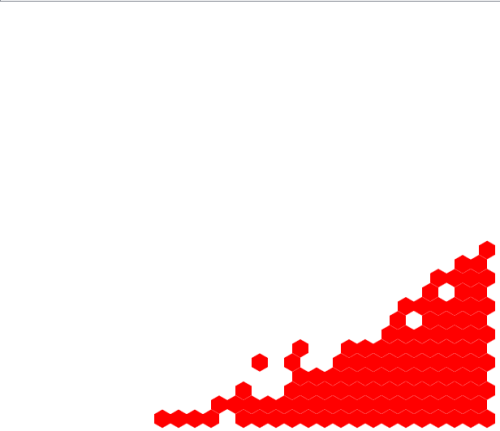Gravitáció és egy vízszintes erőhatás.Abban az esetben, ha a teret egy forgó edény függőleges metszeteként képzeljük el, akkor a forgástengelytől való távolság négyzetével arányos, kifelé egyre növekvő erőhatás, valamint a gravitáció lefele ható állandó hatások következtében megkapjuk az ismert parabola felszínhez hasonló alakzatot:
Forgó folyadék metszet, parabola felszín.Nézzük meg az első feladat (darázsmodell) egy lehetséges megoldásának tervét! Mint korábban említettük: nem titkolt szándékunk, hogy mintát adjunk szimulációs programok készítéséhez.
Ezzel kapcsolatban először is el kell dönteni, hogy a program mit és hogyan jelenítsen meg! A szimuláció során mindig látni kellene a darazsak aktuális elhelyezkedését,
Darazsak eloszlása a dobozokban.valamint számát az egyes dobozokban (sorokban).
Darazsak dobozonkénti darabszáma (piros oszlopok).Emellett lehetséges, hogy egy grafikon mutassa a darázsszám változását az első dobozban (legalább az utolsó valahány időegységben). A szimuláció közben praktikus, ha lehet kérni olyan összesítő oszlopdiagramot, amely a darazsak eloszlását mutatja.
A fejezet lezárásaként megadjuk a program algoritmusvázlatát.
A legfontosabb adatok:
Típus Üzemmód=(Csendes,Folytonos,Lépésenként,Összesít)
A lehetséges üzemmódok:
Változó D: Tömb(1..N:1..2)
S: Tömb(1..N:Egész)
T: Egész
Funkció: Üzemmód
A végrehajtás legfelsőbb szintje:
Program:
Tájékoztató
Ciklus amíg szükséges
Kezdeti értékek beállítása
Paraméterek beolvasása
Idő:=1
Kezdőábra kirajzolása
Ciklus amíg szükséges
Szimulációs lépés
Idő:=Idő+1
Eredmény megjelenítés
Ciklus vége
Kísérlet összesítés
Ciklus vége
Kísérletsorozat összesítés
Program vége.
A hivatkozott eljárásokról, függvényekről a következőket kell tudni!
Tájékoztató:
[A tájékoztató szövegének beolvasása file-ból és megjelenítése.]
Eljárás vége.
Kezdeti értékek beállítása:
AlsóSor:=...; ElsőOszlop:=...; UtolsóOszlop:=...
Kicsinyités:=1; Funkció:=Folyamatos [Kezdeti üzemmód]
Eljárás vége.
Paraméterek beolvasása:
Be: N,A
D(1..A):=(1, ,1); D(A+1..N):=(2, ,2)
S(A):=1
Eljárás vége.
Kezdőábra kirajzolása:
[a főképernyő kirajzolása]
Eljárás vége.
Szimulációs lépés:
i:=véletlen(N); D(i):=3-D(i)
Ha D(i)=1 akkor A:=A+1 különben A:=A-1
S(A):=S(A)+1
Eljárás vége.
Eredmény megjelenítés:
[a fő képernyő változó részeinek kitöltése: "idő", "1-es doboz", illetve a "doboz-ábra" és a "grafikon"]
Eljárás vége.
Szükséges:
Szükséges:=Igaz
Funkció:=FunkcióFigyelés
Elágazás
Funkció=Összesítés esetén Összesítés
Funkció=Vége esetén Szükséges:=Hamis
Funkció=Lépésenként esetén Várakozás
Elágazás vége
Eljárás vége.
A program további részeit és szintjeit már nem részletezzük!
 |
 |
 |
| Készült az "Országos koordinációval a pedagógusképzés megújításáért” című TÁMOP-4.1.2.B.2-13/1-2013-0007 pályázat keretében. (ISBN 978-963-284-631-6) | ||
A tananyag az ELTESCORM keretrendszerrel készült