A síkbeli diffúziós modellek az előző fejezet ötletének kibővítésére épülnek. Legyen a vizsgált térrész egy NxM-es négyzetráccsal lefedett sík és egy-egy cella vagy tartalmazzon egy molekulát, vagy legyen üres!
A szimulációs tér változása annyiból álljon, hogy egy véletlenszerűen kiválasztott molekulát és egyik szomszédját cseréljük fel! Valódi mozgás természetesen csak akkor történik, ha az egyik helyen volt molekula, a másikon pedig nem. A valós rendszertől különbözik modellünk (és sok további modell is) abban, hogy egy molekulának minden lépésben újra választunk irányt (és később sebességet is), azaz az egyedi jellemzőket csupán átlagos eloszlásukkal helyettesítjük. Ezzel imitáljuk a molekulák ütközéséből származó sebesség- és irányváltozásokat.
Jelölje T(N,M) karakterelemű mátrix a táblázatot, ahol a kétdimenziós diffúziót nyomon követjük, '*' a molekulát, szóköz az üres helyet!
Diffúzió:
(i,j):=véletlen hely(N,M)
(k,l):=véletlen szomszéd belül(i,j)
Csere((i,j),(k,l))
Eljárás vége.
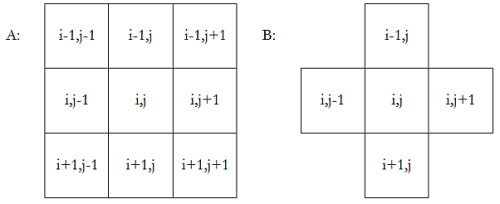
Meg kell jegyeznünk, hogy ez egy furcsa geometriájú tér, ugyanis a szomszédválasztás megvalósítása ábrázolásfüggő. (Ld. a következő ábrát!) Itt az A esetben az átlós szomszédok és az oldalszomszédok is 1 egység távolságra vannak, a B esetben pedig az oldalszomszédok 1, az átlós szomszédok viszont 2 egységre, holott az 1 egységnyi befogójú egyenlőszárú derékszögű háromszög átfogójának hossza négyzetgyök 2.
A továbbiakban a könnyebb kezelhetőség kedvéért a modellt egy kicsit módosítjuk. Vegyük körül a vizsgált teret fallal, azaz minden helyen háromféle dolog fordulhasson elő: molekula, üres hely, valamint fal. A fal – ezt tetszőleges, másra nem használt táblaérték, most: jel, reprezentálhat – bevezetése lehetővé teszi, hogy szomszédválasztásnál ne kelljen külön törődni a táblázat szélével, ugyanakkor megteremti annak lehetőségét is, hogy tetszőleges alakú sík teret vizsgálhassunk.
Ezen változtatások figyelembevétele után a szimulációs lépés a következőképpen módosul:
Diffúzió:
(i,j):=véletlen hely(N,M)
(k,l):=véletlen szomszéd(i,j)
Csere((k,l),(i,j))
Eljárás vége.
véletlen hely(N,M):
Ciklus
i:=véletlen(N); j:=véletlen(M)
amíg (i,j) fal
Ciklus vége
véletlen hely:=(i,j)
Függvény vége.
véletlen szomszéd(i,j):
Ciklus
k:=véletlen(i-1…i+1); l:=véletlen(j-1…j+1)
amíg (k,l) fal vagy (k=i és l=j)
Ciklus vége
véletlen szomszéd:=(k,l)
Függvény vége.
Ezzel a szimulációs lépéssel csak vizuálisan figyelhető meg a molekulák egyenletes eloszlása. Mit lehetne tenni e tulajdonság adminisztrálása érdekében?
A megoldás filozófiája igen egyszerű: induljunk ki valamilyen rendezett konfigurációból (az eseménytérnek egy szabályos darabkáját töltsük föl részecskékkel), majd vizsgáljuk időről-időre a diffúzió okozta entrópia változást! Az entrópia tényleges kiszámolása helyett (amely meglehetősen lelassítaná a szimulációt) egy olyan globális jellemzőt válasszunk, amely nyomon követése nem jelent különösebb nehézséget! Az entrópia szerepébe az alakzat (a részecskék alkotta konfiguráció) szabad felszínét helyettesítsük. Ez a változás lehetőségével arányos mennyiség, vagyis – hozzávetőlegesen – megfelel az entrópia által kifejezett bizonytalanság mértékének. (Ti. hogy mennyire tekinthető valószínűnek a jelen helyzet. A legkevésbé váratlan az a konfiguráció, amelyben a részecskék egyenletesen töltik ki a rendelkezésre álló teret, valószínűtlen az, amely valamilyen szabályosságot mutat; az előző szabad felszíne maximális, az utóbbié – a szabályosságtól függően – akár minimális is lehet.) A megvalósításhoz csupán egy üres szomszédok száma függvényt kell újólag megírnunk; a lényeg csak ennyivel módosul:
Diffúzió:
(i,j):=véletlen hely(N,M)
(k,l):=véletlen szomszéd(i,j)
Elágazás
T(i,j)="*" és T(k,l)=" " esetén Sz:=1
T(i,j)=" " és T(k,l)="*" esetén Sz:=-1
egyéb esetben Sz:=0
Elágazás vége
Szf:=Szf-Sz*üres szomszédok száma(i,j)
Csere((i,j),(k,l))
Szf:=Szf+Sz*üres szomszédok száma(k,l)
Eljárás vége.
üres szomszédok száma(i,j):
U:=0
Ciklus (i1,j1)=(i-1,j-1)-től (i+1,j+1)-ig
Ha T(i1,j1)="*" akkor U:=U+1
Ciklus vége
Ha T(i,j)="*" akkor U:=U-1
üres szomszédok száma:=U
Függvény vége.
Ezzel a szimulációs lépéssel befejezzük a molekulák kölcsönhatás nélküli eloszlásának vizsgálatát. Ez a modell is meggyőzően igazolja az előző fejezetben már kimondott állítást, miszerint a legvalószínűbb eloszlás az egyenletes eloszlás lesz! (Egy tetszőlegesen kijelölt térrészre itt is teljesülnek a stabilitást okozó 2. elemi modell (S-,S+) feltételei.)
Lépjünk tovább a síkbeli diffúziók vizsgálatában! Vezessük be a modellbe a gravitáció jelenségét! A korábbiakból tudjuk, hogy ilyenkor a szomszédválasztást kell befolyásolni, mégpedig lefelé nagyobb valószínűséggel kell szomszédot választani, mint felfelé. A jobboldali vagy a baloldali szomszéd választását ez a jelenség – modellünkben – nem befolyásolja. Így a fel-vízszintesen-le irányú választás valószínűsége a következőképpen módosul: a gravitációmentes 1/3–1/3–1/3 arány helyett gravitáció figyelembevételekor az 1/3-G—1/3—1/3+G arányokat vesszük.
Rögvest mindenkiben fölmerül az a kérdés, hogy mi köze van a fenti képletben használt G valószínűségnek a nehézségi gyorsulás g értékéhez! Próbáljunk kapcsolatot találni e két, látszólag messze eső állandó között! Egyensúlyban konstans sűrűségeloszlás alakul ki. E tényt kihasználva, kétféle számítással lehet meghatározni a sűrűségeloszlás G-től, illetve a g-től való függését, majd e kapott két formulát egyeztetve adhatunk választ a fölvetett kérdésre.
Íme, a szokásos fizikai megközelítés: Az ismert ún. barometrikus magasságformula ad egyrészről támpontot.
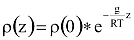
ahol ρ→sűrűség, z→magasság, g→gravitációs gyorsulás együtthatója – tegyük fel, hogy nem függ a magasságtól! –, R a specifikus gázállandó, T abszolút hőmérséklet (legyen ez is állandó a vizsgált magasságintervallumon).
A modellben a sűrűség alakulását – egyensúly esetén a z szintre ugyanannyi érkezik fölülről, mint távozik fölfelé – az alábbi formulával írhatjuk le:
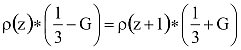
Innen adódik a
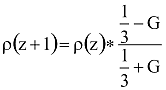
formula. Ebből elemi úton megkapható a könnyebben átlátható, nem rekurzív formula:
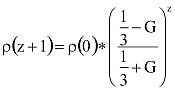
A formulák egybevetése után az
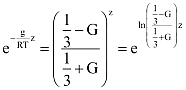
kapcsolatot használhatjuk föl a G és g közötti hozzávetőleges(!) összefüggés megállapítására. Újabb elemi átalakítások után kijön a keresett formula:
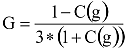
ahol
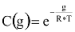
Érdekesség kedvéért nézzük meg a G-t először, mint T, majd mint g függvényét!
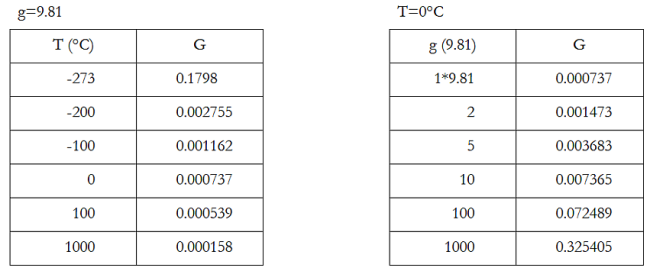G értékei kiszámolása.Most, miután igazoltnak látjuk az ötletünket, nézzük meg ennek algoritmizálását! (Ahogy korábban is rajzoltuk: a táblázat sorait fentről lefelé sorszámozzuk.)
Szimulációs lépés:
(i,j):=véletlen hely(N,M)
(k,l):=véletlen szomszéd(i,j)
Csere((i,j),(k,l))
Eljárás vége.
véletlen szomszéd(i,j):
Ciklus
l:=véletlen(j-1…j+1); A:=véletlenszám
Elágazás
A<1/3-G esetén k:=i-1 [felfelé]
1/3-G≤A<2/3-G esetén k:=i [oldalt]
egyéb esetben k:=i+1 [lefelé]
Elágazás vége
amíg (k,l) fal vagy (k=i és l=j)
Ciklus vége
véletlen szomszéd:=(k,l)
Függvény vége.
Itt látható, hogy a gravitációs hatást a szomszéd hely választásánál vettük figyelembe. Amikor mind a két kiválasztott helyen molekula áll, célszerű a cserét meg nem történtnek nyilvánítani, hisz ilyen esetben a (k,l) helyen levő a gravitációs hatásra pont ellentétesen reagál. A kettős cserék elkerülésének másik módja az lehetne, hogy addig keresünk új és új szomszédot, míg üres helyet nem találunk. Figyelmes Olvasóink azonban rögtön rájönnek, hogy ez nem mindig vezetne jóra, hisz elképzelhető – elég nagy sűrűség esetén nagyon gyakran –, hogy egy molekulának csak molekula szomszédja van. Ebben az esetben a véletlen szomszéd(i,j) eljárásunk végtelen ciklusba kerülne, ami nem lehet célunk.
Ezt a modellünket bővíthetjük úgy is, hogy a gyorsulásnak ne csak a függőleges irányú komponensét, hanem a vízszintest is figyelembe tudjunk venni. Ez például gyorsuló folyadékok felszínének vizsgálatát teszi lehetővé. További fejlesztési lehetőség, hogy egy kiválasztott cellában számolt gyorsulás mértéke mondjuk a középső oszloptól, mint tengelytől való távolságtól is függjön. Ezen hatások figyelembevételét a véletlen szomszéd eljárásban lehet valamilyen módon megoldani. (A tettre kész Olvasóra bízzuk az eljárások megírását!)
A következő vizsgált jelenség legyen a „szél”! A legegyszerűbb megvalósításban tulajdonképpen azt kell megoldani, hogy a molekulák rendelkezzenek egy „szélirányú” sebességkomponenssel is. Mivel egyedi sebességvektorokat nem tárolunk, ezért ez úgy oldható meg, hogy valószínűbbé tesszük abba az irányba az elmozdulást, amerre a szél „fúj”, s kisebb valószínűségűvé az ellenkező irányú elmozdulást. Lényegében tehát ugyanazt kellene tenni, mint a gravitáció esetében. Egyetlen lényeges különbség azonban mégis van: a molekulák nem torlódhatnak fel a vizsgált térrész egyik szélén, s nem tűnhetnek el a másik széléről. Ennek következtében nem szabad zártként vizsgálni a rendszert, hanem át kell térni nyílt rendszerekre.
Két megoldandó részfeladat lesz: az egyik a molekulák kilépése a vizsgált rendszerből, a másik pedig a belépés. A kilépést egyszerűen megoldhatjuk: ha a molekula el „akarja” hagyni a vizsgált térrészt, akkor engedjük ki. A belépés kicsit bonyolultabb: megadjuk azt, hogy a vizsgált tér szélein milyen relatív gyakorisággal található molekula. (Ez a szimuláció során legyen állandó érték!) S ez már a mozgás szabályainak figyelembevételével léphet be a rendszerbe. Ez a relatív gyakoriság függhet a magasságtól (gondoljunk a gravitációt tartalmazó modellekre)!
Diffúzió:
(i,j):=tágabb véletlen hely(N,M)
(k,l):=véletlen szomszéd(i,j)
Elágazás
(i,j) kívül és (k,l) belül esetén Belépés(k,l)
(i,j) belül és (k,l) kívül esetén Kilépés(i,j)
(i,j) belül és (k,l) belül esetén Csere((i,j),(k,l))
Elágazás vége
Eljárás vége.
A Belépés, illetve a Kilépés (valamint a tágabb véletlen hely) eljárások megírását – egyszerűségük miatt – ismét Olvasóinkra hagyjuk.
A be- és kilépést másképp is megoldhatjuk, ha a szimulációs teret a következőképpen képzeljük el:
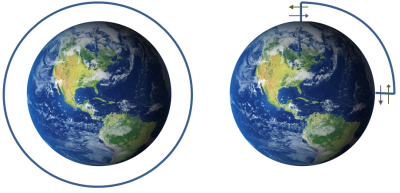A szimulációs tér a Föld körül.Az első esetben a szimulációs tér körbeéri a Földet, így ami a szimulációs tér egyik szélén kilép, az a másik szélén belép. A második esetben a szimulációs tér nem ér körbe a Földön. Ilyenkor viszont feltételezhetjük, hogy az egyik oldalon kilépés és a másik oldalon belépés eloszlása egyforma.
Tehát mindkét esetben a megoldás: az első és az utolsó oszlop legyenek egymás szomszédjai!
Az eddigi módosításainknak az volt a célja, hogy egyre valósághűbb modelleket kapjunk. A következő bonyolításnak is az a célja, hogy a légkör egy függőleges metszetében tartózkodó molekulák valóságosabb mozgását, viselkedését meg tudjuk vizsgálni. A középiskolai tanulmányokból biztosan mindenki emlékszik arra, hogy minél magasabban vagyunk, annál alacsonyabb a levegő hőmérséklete. Vizsgáljuk most meg, hogy hogyan tudnánk a molekulák mozgékonyságának, azaz a hőmérsékletnek a változását szimulálni!
Lehetőségek:
A hőmérséklet bevezetését egy harmadik módon is megtehetjük. Most a hőmérsékletet az elmozdulás távolságával hozzuk kapcsolatba. Első közelítésben az egyszerűség kedvéért csalunk: az (i,j) ponttól az (i-1,j) ugyanolyan távolságra lesz, mint az (i-1,j-1). Ekkor a véletlen szomszéd választást kell módosítani! Tartalmazza Táv(i) az i. sorban levő molekulák maximális lehetséges elmozdulási távolságát, s ez legyen egész szám! Tegyük föl továbbá, hogy a molekulák sebességeloszlása egyenletes eloszlást követ (bár ki fog derülni: ez korántsem igaz). (A korábbi esetekben Táv(i)=1 állt fenn mindig.)
véletlen szomszéd(i,j):
Ciklus
k:=véletlen(i-Táv(i)…i+Táv(i))
l:=véletlen(j-Táv(i)…j+Táv(i))
amíg (k,l) fal vagy (k=i és l=j)
Ciklus vége
véletlen szomszéd:=(k,l)
Függvény vége.
Pontosítsuk az ötletet, amivel még közelebb kerülünk a valóságos rendszerekhez. A molekulák mozgását nem csak véletlen helyválasztással befolyásoljuk, hanem az elmozdulás nagyságát is meghatározzuk, ami nyilván a sebességre jellemző mennyiség.
Ebben az elképzelésben azt kell megfontolni, hogy a nagyobb távolságra való cserénél mi legyen a közbülső, átugrott helyekkel. Elképzelhető ugyanis, hogy azokon is van molekula, amelyek a hosszabb lépést megakadályozhatnák. Mivel ebben az ideális rendszerben az ütközéskor a sebességek gazdát cserélnek (azonos tömegűek és az ütközés rugalmas), s számunkra nem megkülönböztethetők a tömegek, ezért efelett a probléma felett minden további nélkül keresztülsiklunk.
A sebességvektor nagyságával kapcsolatos követelményeket úgy elégíthetjük ki, hogy az elmozdulás távolságára a Maxwell-Boltzmann (sebesség) eloszlás alapján választunk értéket. Az irány figyelembevételére pedig egy irányt kell választani, s abból kiszámolni az elmozdulást.
véletlen szomszéd(i,j):
Ciklus
(u,v):=Maxwell(táv(i))[a sebesség két komponense]
k:=u+i; l:=v+j
amíg (k,l) fal vagy (k=i és l=j)
Ciklus vége
véletlen szomszéd:=(k,l)
Függvény vége.
A mozgékonyság bevezetését más úton is megoldhatjuk. A hőmérsékletet most az elmozdulás valószínűségével hozzuk kapcsolatba. Tehát Moz(i) jelentse annak a valószínűségét, hogy a kiválasztott molekula elmozdulhat. (Az i itt is a függőleges a koordináta.) Így a szimulációs lépés a következőképpen alakul:
Diffúzió:
(i,j):=véletlen hely(N,M)
(k,l):=véletlen szomszéd(i,j)
Ha T(i,j) molekula és T(k,l) üres és véletlenszám<Moz(i)
akkor Csere((k,l),(i,j))
Eljárás vége.
Ezzel a megoldással az a probléma, hogy az előző modellnél lényegesen lassúbb futást eredményezhet, ha az egyes helyekhez kis sebességet rendeltünk.
Első elképzelésünk szerint a hőmérséklet változzon a magassággal egy Höm(i) függvény szerint! (Az i jelölje a szimulációs tér kiválasztott pontjának függőleges koordinátáját!) Egy adott térrész hőmérsékletét a benne tartózkodó molekulák sebessége határozza meg, tehát ezt az új hatást bevezethetjük azzal, hogy a molekulák „mozgékonyságát”, azaz kiválasztásuk gyakoriságát növeljük, vagy csökkentjük a hőmérsékletet leíró függvény szerint. Ezért a diffúziós lépést úgy módosítjuk, hogy a Höm(i) függvény szerint változó valószínűséggel kell kiválasztani az éppen mozgó molekula magasságkoordinátáját.
Diffúzió:
i:=véletlen magasság(N,H()); j:=véletlen(M)
(k,l):=véletlen szomszéd(i,j)
Ha T(i,j) molekula és T(k,l) üres akkor Csere((k,l),(i,j))
Eljárás vége.
A véletlenszerű magasságválasztást a teljes eseményrendszerből – a lehetséges sorokból – való kiválasztás szokásos algoritmusával végezzük. A választásban fölhasználtuk a következő formulákkal definiált (s már korábban kiszámolt) valószínűségvektort:
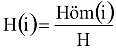
ahol
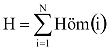
Legyen pl. a kapcsolatot leíró függvény ν:hőmérséklet→mozgékonyság, ekkor
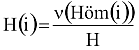
ahol
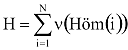
Nagyon ritka eset azonban, amikor a molekulák sebességét egyértelműen helyhez lehet kötni – pl. melegítjük néhány pontján a teret. Más sebességeloszlás esetén nagyon bonyolult lesz a sebességgel arányos választás, így más megoldás után kell néznünk.
Egy ennél valósághűbb modellt kapunk, ha az egyes molekulákhoz rendelünk sebességet. Ekkor:
Szimulációs lépés:
x:=véletlen(DB)
i:=Mol(x).sor; j:=Mol(y).oszlop
(k,l):=véletlen szomszéd belül(i,j)
y:=T(k,l)
Csere((k,l),(i,j))
Mol(x).sor:=k; Mol(x).oszlop:=l
Ha y>0 akkor Mol(y).sor:=i; Mol(y).oszlop:=j
Eljárás vége.
Bármelyik algoritmust is választjuk az előbbiekből a hőmérséklet hatásának vizsgálatára, megfigyelhetjük, hogy a „melegebb” területen levő molekulák mozgékonyabbak, mint a „hidegebbek”, azaz ezeken a területeken kisebb a sűrűség. Amennyiben a hőmérséklet-eloszlás viszonylag nagy területeken állandó, akkor érdemes ezen területekhez tartozó molekulaszámot nyilvántartani és megjeleníteni.
Az eddig vizsgált univerzumainkra jellemző volt, hogy benne az erő, amely a teljesen véletlenszerű mozgást valamelyest determinizálta, meglehetősen speciális volt: vagy sem a helytől, sem az időtől nem függött, vagy a függés nagyon szabályos volt (pl. a gravitációs modellnél). Ez tette lehetővé, hogy egyszerű volt a számításba vétele. Ennek a fejezetnek éppen az a célja, hogy az erőnek egy általánosabb fogalmát bevezesse modelljeinkbe. Az absztrakciónak két lehetséges útját járjuk be (helyesebben indulunk el rajta). Az egyik az, amelyben elvetjük a „helybeli” állandóságot, szabályosságot. A másik az időbeli változatlanságot ejti el.
Ha az erő különösebb szabályosságot nem mutatva hat, vagyis az erőtér inhomogénnek tekinthető, akkor ennek figyelembevétele úgy történhet, hogy
A1. Minden mozgásba lendülő részecskére ható erőt minden egyes alkalommal újraszámoljuk. A megvalósítás mintájául a 2.3.B-beli algoritmus szolgálhat.
Diffúzió:
(i,j):=véletlen hely(N,M)
(k,l):=véletlen szomszéd(i,j)
Ha T(i,j) molekula és T(k,l) üres és véletlenszám<Moz(i,j)
akkor Csere((k,l),(i,j))
Eljárás vége.
A Moz(i,j) ez esetben egy függvény, amely azt „valószínűsíti”, hogy a molekula az (i,j) pontból kimozdulhat. A valószínűség nyilván annál nagyobb, minél nagyobb az adott pontban kiszámolt térerő. (Megjegyezzük, még sokféle értelmezés elképzelhető. Pl. az erőhöz irányt is rendelhetünk, ekkor a Moz függvény paraméterezendő a (k,l)-lel is, és arra ad választ, hogy (i,j)-ből (k,l)-be lépés mennyire hihető.) Ez az elképzelés nyilván időben elég hosszadalmas. Ezen segít a következő:
A2. Mivel időben nem változó a tér, ezért ha már egyszer kiszámoltuk egy pontban a térerő nagyságát, akkor ugyanitt többet nem lenne e bonyolult számításra szükség, feltéve, hogy följegyezzük. Nosza, vegyünk föl egy második teret a molekulatér (kifejezőbb szóval: mozgástér) mellé, amelyben pontról pontra az érvényes térerőt adminisztráljuk (ez természetesen lehet skalár, de lehet vektormennyiség is akár – ahogy már láttuk). Így a függvénykiértékelés helyett mindössze egy mátrixérték-hivatkozás szerepelne a fenti algoritmusban. (Igaz, a szimulációt megelőzően e háttérteret föl kell tölteni.) Látszik e megoldás az időszükségletet helyigényre váltja.
Ha az erőtér időben mutat változatosságot, dinamizmust, akkor is alkalmazható az előző (A1.) pontbelihez nagyon hasonlító eljárás: csak most a kiszámítás nem (vagy nem csak) helykoordinátáktól függ, hanem az aktuális időtől (is):
Diffúzió(Idő):
(i,j):=véletlen hely(N,M)
(k,l):=véletlen szomszéd(i,j)
Ha T(i,j) molekula és T(k,l) üres és véletlenszám<Moz(Idő)
akkor Csere((k,l),(i,j))
Eljárás vége.
A vizsgálatunkban előforduló erőterek rendelkeztek egy furcsa tulajdonsággal. Nevezetesen: valamilyen külső erőforrás indukálta, ami a „mozgástértől” teljesen függetlenül hatott a molekulákra. A valóságos univerzumokban általában nem ez a helyzet. Az a modell tekinthető tipikusnak, amelyben a részecskék mozgását nem csupán egy külső erőforrás vezényli, hanem amelyben a molekulák egymással is kontaktusba kerülnek: mintha mindegyik saját erőteret hozna létre. Ebben az esetben is az A. paragrafus két lehetősége áll rendelkezésünkre:
B1. Minden pillanatban a kérdéses pontban az érvényes erőket újra meg újra ki kell számítani. Mivel feltételezésünk szerint minden molekulára minden más molekula hatással van, ezért egyetlen szimulációs lépésben N*(N-1) egyedi erőhatást kell kalkulálnunk. Ez igen számolásigényes, sőt beláthatóan nagyon nem előrelátó. Olyan erőkomponenseket is újból kiszámol, amelyeket egy korábbi számításban is már meghatározott: két azonos távolságban maradt molekula egymásra hatása nem változik), mi mégis másodszor (sokadszor) is kiszámítjuk. Ez az „amnézia” a modell lényegéből fakad, ezért semmi meglepő sincs benne. Az erő-valószínűség függvény kalkulálásánál legfeljebb a számításba veendő molekulák megtalálása gond. Kézenfekvő – bár korántsem hatékony – megoldás a teljes tér végigpásztázása. A diffúzió A1-beli eljárása itt az alábbi függvényre épít:
Moz(i,j):
erő:=0
Ciklus (ii,jj)=(1,1)-től (N,M)-ig
Ha T(ii,jj) molekula akkor erő:=erő+f((i,j),(ii,jj))
Ciklus vége
Moz:=erő
Függvény vége.
A Moz függvényben található f függvény valamilyen normalizált összefüggése két adott koordinátájú pont között ható erőnek. (Ugyanis az eredmény egy valószínűség kell legyen.)
B2. A modellt emlékezettel látjuk el úgy, hogy a „mozgástér” mellett az erők terét is tároljuk. Ezen csak akkor kell módosítanunk – a kezdeti inicializálás után –, ha változás állt be a „mozgástérben”, sőt ekkor is csak egyetlen – az elmozdult – molekula erőtér-módosulását kell végigvezetnünk az erők terén. Igaz ez most – lévén minden pontra ki kell számítani a módosult térerőt – N*M erőkomponens számolását jelenti. Cserében a szemlélethez közelebb álló világot kaptunk: az üres helyen is jelen van az erőtér, csak éppen hatástalan.
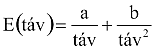
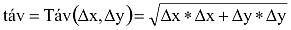
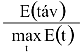
Egy továbblépési lehetőség lehetne az, ha a molekulák számát jelentősen csökkentenénk (pl. 2-re vagy 3-ra), a méretüket pedig ugyanilyen jelentősen megnövelnénk. Ekkor már nem lehetne elhanyagolni a köztük levő vonzóerőt, sőt a mozgásukat éppen ez határozná meg. Ebből keletkezhetnek többek között a bolygómozgás modelljei.
Az eddigi diffúziós modelljeink nagy hibája, hogy nagyon lassúak. Ezen segíthetünk a következő módosítással. Vizsgáljuk újra a legelső síkbeli diffúziós modellt! A módosítás lényege: tároljuk minden egyes molekula helykoordinátáját is, s amikor választunk, akkor molekulát válasszunk és ne helyet! Jelölje Mol(i).x az i. molekula x-koordinátáját, Mol(i).y az y-koordinátát, DB pedig a molekulák számát! A táblázat most számokat tartalmazzon: ahol nincs molekula, ott 0-t, ahol van, ott pedig a molekula sorszámát!
Diffúzió:
s:=véletlen(DB); i:=Mol(s).x; j:=Mol(s).y
(k,l):=véletlen szomszéd(i,j)
Ha (k,l) üres akkor Csere((k,l),(i,j)); Mol(s).x:=k; Mol(s).y:=l
Eljárás vége.
Ezzel a megoldással elkerüljük az üres-üres és a molekula-molekula cseréket, ami egy ritkán vagy sűrűn kitöltött rendszer esetén bizony elég gyakran előfordulhatna. Természetesen a fejezet összes modellje ezzel az ötlettel felgyorsítható. (A „szeles” modell esetén bonyolódik a dolog, a ki- és belépés miatt.)
Ilyen ábrázolás esetén lehetővé válik, hogy a molekulákhoz egyedi sebességet rendeljünk, s a véletlen szomszédválasztás helyett ezt alkalmazzuk a mozgás során.
Diffúzió:
s:=véletlen(DB); i:=Mol(s).x; j:=Mol(s).y [az s. helye]
k:=i+Mol(s).vx; l:=j+Mol(s).vy [az s. sebessége]
Ha (k,l) üres akkor Csere((k,l),(i,j)); Mol(s).x:=k; Mol(s).y:=l
különben Ütközés(s,i,j,k,l)
Eljárás vége.
Meggondolandók: Néhány problémát az algoritmus fenti szintje nem fogalmaz meg tisztán, amikről alacsonyabb szinten pedig dönteni kell. Így pl.:
 |
 |
 |
| Készült az "Országos koordinációval a pedagógusképzés megújításáért” című TÁMOP-4.1.2.B.2-13/1-2013-0007 pályázat keretében. (ISBN 978-963-284-631-6) | ||
A tananyag az ELTESCORM keretrendszerrel készült